This is the second problem of Div.3. But I think it is not easy.

Problem:1029B - Creating the Contest

Simple Meaning of Problem:

There is a sequence a and you should choose the longest sequence b {a_i1, a_i2, ..., a_ip} (p is the length of b) such that:each j∈[1, k) a_ij + 1 ≤ a_ij·2 should hold.

print the maximum number of p (the length of b)

First, you can enumerate which ones to choose. You will get a algorithm with O(2ⁿ). And you will get a Time Limit Exceed.(I didn't write it, because it is valueless.)

Then, dp is another useful algorithm. So we can try to use dp.

f[i] means that if you choose the number a_i, you can get the maximum p (only of 1 to i).

It is very easy to get the state transition equation:

f[i] = max{f[j]} + 1, j satisfy that a_i ≤ a_j·2 and j ≤ i.

And the answer is max{f[i]} (i is 1 to n).

code:42093398

#pragma comment (linker,"/STACK:1024000000") 
#pragma GCC optimize(2)
#pragma GCC target(arch=corie7-acx)
#include<bits/stdc++.h>
using namespace std;
int n,a[200001],f[200001];
deque <int> q;
int t,ans;
int main()
{
	scanf("%d",&n);
	for (int i=1;i<=n;i++)
	scanf("%d",&a[i]);
	f[1]=1;
	for (int i=2;i<=n;i++)
	{
		for (int j=1;j<=i-1;j++)
		if (a[j]*2>=a[i]) f[i]=max(f[i],f[j]);
		f[i]++;
	}
	for (int i=1;i<=n;i++)
	ans=max(ans,f[i]);
	printf("%d",ans);
	return 0;
}

And this code does better:42095786(In fact, it also Time Limit Exceed on Test 4)

#pragma comment (linker,"/STACK:1024000000") 
#pragma GCC optimize(2)
#pragma GCC target(arch=corie7-acx)
#include<bits/stdc++.h>
using namespace std;
int n,a[200001],f[200001];
deque <int> q;
int t,ans;
int main()
{
	scanf("%d",&n);
	for (int i=1;i<=n;i++)
	scanf("%d",&a[i]);
	f[1]=1;
	for (int i=2;i<=n;i++)
	{
		for (int j=i-1;j>=1;j--)
		if (a[j]*2>=a[i]) f[i]=max(f[i],f[j]);
			else break;
		f[i]++;
	}
	for (int i=1;i<=n;i++)
	ans=max(ans,f[i]);
	printf("%d",ans);
	return 0;
}

But, unfortunately, these two are both Time Limit Exceed. (Actually, it is inevitable.)

Because when a_n ≤ a₁·2, the time complexity of the code will come to O(n²) (break is useless).

So it is inevitable that the code will TLE.

Now, how can we optimize our algorithm?

In the problem, notice that the numbers are increasing.

So when i is increasing, a_i is increasing, too. And 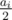is increasing, so the number which is less than 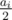is also increasing.

Because of this, for the increasing number i, the j which is satisfy a_i ≤ a_j·2 is increasing as well.