Thank you for participating in this round! Problems A and G are authored by Cocoly1990 and the rest by me.
Currently, I'm not sure if the editorials are fine enough. Please feel free to tell me where I can improve.
| A | B | C | D | E | F | G | H | I | |
|---|---|---|---|---|---|---|---|---|---|
| _istil | 800 | 1200 | 1400 | 1700 | 1900 | 2500 | [2800, 3300] | 3200 | [800, 3000] |
| Cocoly1990 | 800 | 1300 | 3000 | ||||||
| TheScrasse | 800 | 1200 | ? | 1800 | 2500 | 3000 | 3000 | 3500 | |
| LMydd0225 | 800 | 1300 | 1600 | 1900 | 2100 | 2400 | 2800 | 2900 | [2500, 3200] |
| Error_Yuan | 900 | 1200 | 1400 | 2000 | 2100 | 2500 | 3000 | 3200 | |
| Caylex | 800 | 1300 | 1500 | 1900 | 2200 | 2600 | [2500, 3100] | ||
| tzl_Dedicatus545 | 800 | 1000 | 1100 | 1400 | 2300 | ||||
| PaciukZvichainyi | 800 | 1200 | 1500 | 1800 | 2100 | 2500 | |||
| doujinshi_master | 800 | 1200 | 1500 | 1800 | |||||
| juan_123 | 800 | [800, 1100] | 1000 | 1700 | 2400 | 2800 | [2700, 3500] | ||
| StarSilk | 800 | 1300 | 1400 | 1700 | 2500 | 3100 | 2700 | ||
| SkyWave2022 | 800 | 1200 | 1600 | [1600, 1900] | |||||
| ABitVeryScaredOfWomen | 800 | 1200 | 1500 | 1800 | 2100 | ||||
| FFTotoro | 800 | 1200 | 1400 | 1900 | 1900 | 2400 | 2900 |
Can you find a partition that is always valid?
Suppose you are given a set $$$S$$$. How do you judge whether $$$S$$$ is stable in $$$\mathcal O(\lvert S\rvert)$$$?
Are sets that are very large really necessary?
Note that: we always have a partition like $$$[a_1], [a_2], \dots, [a_n]$$$, since $$$(x, x, x)$$$ always forms a non-degenerate (equilateral) triangle.
We focus on the second partition scheme in which not all continuous subsegments have a length of $$$1$$$. One can also note that if a set $$$S$$$ is stable then for all $$$T \subsetneq S$$$ ($$$T \neq \varnothing$$$), $$$T$$$ is also stable.
- Short proof: If $$$\exists u, v, w \in T$$$ such that $$$(u, v, w)$$$ doesn't form a non-degenerate triangle, therefore $$$u, v, w \in S$$$ so it is concluded that $$$S$$$ is not stable. Contradiction!
If such a partition exists, we can always split long continuous subsegments into shorter parts, while the partition remains valid. Therefore, it's enough to check the case in which there is one subsegment of length $$$2$$$ and the rest of length $$$1$$$. So, we should output NO if and only if for all $$$1 \leq i < n$$$, $$$2\min(a_i, a_{i+1}) \leq \max(a_i, a_{i+1})$$$.
#include <bits/stdc++.h>
#define MAXN 1001
int a[MAXN];
void solve() {
int n; std::cin >> n;
for (int i = 1; i <= n; ++i) std::cin >> a[i];
for (int i = 1; i < n; ++i) if (2 * std::min(a[i], a[i + 1]) > std::max(a[i], a[i + 1]))
{ std::cout << "YES\n"; return; }
std::cout << "NO\n";
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr), std::cout.tie(nullptr);
int t; std::cin >> t; while (t--) solve(); return 0;
}
2053B - Outstanding Impressionist
What if for all $$$1 \leq i \leq n$$$, $$$l_i \ne r_i$$$ holds? How do you prove it?
Use prefix sums or similar to optimize your solution.
For each $$$1 \leq i \leq n$$$, for each $$$l_i \leq x \leq r_i$$$, we want to check if it is okay for impression $$$i$$$ being unique at the value of $$$x$$$. Note that: for each $$$j \neq i$$$, we can always switch $$$w_j$$$ to a value different from $$$x$$$ if $$$l_j \neq r_j$$$, since there are at least two options. Therefore, it is impossible if and only if there exists a $$$1 \leq j \leq n$$$ with $$$j \neq i$$$ such that $$$l_j = r_j = x$$$.
Let's record $$$a_i$$$ as the number of different $$$k$$$ satisfying $$$1 \leq k \leq n$$$ and $$$l_k = r_k = i$$$. If $$$l_i \neq r_i$$$, then we say impression $$$i$$$ cannot be made unique if and only if for all $$$l_i \leq k \leq r_i$$$, $$$a_k \geq 1$$$; otherwise ($$$l_i = r_i$$$), it cannot be unique if and only if $$$a_{l_i} \geq 2$$$.
This can all be checked quickly within a prefix sum, so the overall time complexity is $$$\mathcal O(\sum n)$$$.
#include <bits/stdc++.h>
#define MAXN 400001
int l[MAXN], r[MAXN], sum[MAXN], cnt[MAXN];
void solve() {
int n; std::cin >> n;
for (int i = 1; i <= 2 * n; ++i) sum[i] = cnt[i] = 0;
for (int i = 1; i <= n; ++i) {
std::cin >> l[i] >> r[i];
if (l[i] == r[i]) sum[l[i]] = 1, ++cnt[l[i]];
}
for (int i = 2; i <= 2 * n; ++i) sum[i] += sum[i - 1];
for (int i = 1; i <= n; ++i)
std::cout << ((l[i] == r[i] ? cnt[l[i]] <= 1 : sum[r[i]] - sum[l[i] - 1] < r[i] - l[i] + 1) ? "1" : "0");
std::cout << '\n';
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr), std::cout.tie(nullptr);
int t; std::cin >> t; while (t--) solve(); return 0;
}
Process many segments simultaneously. What kind of segments do we process at a time?
The length.
The point that must be noted is: that if we call the process of splitting a large segment into two smaller segments a round, then all segments are of the same length when the $$$i$$$-th round of the observation is conducted; and, the number of rounds does not exceed $$$\mathcal O(\log n)$$$. The $$$k$$$ restriction is equivalent to specifying that only a certain prefix of rounds is computed.
Here are some different approaches:
- (Most succinctly) Note that the distribution of segments after round 1 is centrally symmetric; Also, $$$x$$$ and $$$y$$$ being centrally symmetric implies that $$$x + y = n + 1$$$, so it is simple to calculate by simulating the number of segments and the length directly.
- If a segment $$$[l, r]$$$ is split into $$$[l, m - 1]$$$ and $$$[m + 1, r]$$$, its left endpoint sum changes from $$$l$$$ to $$$2l + \frac{r - l}{2} + 1$$$, and since $$$(r - l)$$$ is fixed, the sum of the left endpoints of all segments can be maintained similarly.
- The following recursive method also works: the answer to $$$n$$$ can be recovered by the answer to $$$\lfloor \frac{n}{2} \rfloor$$$. The time complexity is $$$\mathcal O(t\log n)$$$.
This is written by _TernaryTree_.
#include <bits/stdc++.h>
#define int long long
using namespace std;
int T;
int n, k;
signed main() {
cin >> T;
while (T--) {
cin >> n >> k;
int mul = n + 1, sum = 0, cur = 1;
while (n >= k) {
if (n & 1) sum += cur;
n >>= 1;
cur <<= 1;
}
cout << mul * sum / 2 << endl;
}
return 0;
}
2053D - Refined Product Optimality
What if $$$q = 0$$$?
How do you keep the array sorted?
The problem makes no difference when both $$$a$$$ and $$$b$$$ can be rearranged. Let the rearranged arrays of $$$a$$$ and $$$b$$$ be $$$c$$$ and $$$d$$$ respectively.
If $$$q = 0$$$, we can write $$$c$$$ as $$$\operatorname{SORTED}(a_1, a_2 \ldots, a_n)$$$ and $$$d$$$ as $$$\operatorname{SORTED}(b_1, b_2 \ldots, b_n)$$$. It can be proved that this reaches the maximum value: if not so, then
- There must be some pair $$$(i, j)$$$ such that $$$c_i < c_j, d_i > d_j$$$.
- Since $$$\min(c_i, d_i) \cdot \min(c_j, d_j) = c_i \cdot \min(c_j, d_j) \leq c_i \cdot \min(c_j, d_i) = \min(c_i, d_j) \cdot \min(c_j, d_i)$$$, we can swap $$$d_i$$$ and $$$d_j$$$, and the product does not decrease.
Consider the modification, which is a single element increment by $$$1$$$. Without loss of generality, let $$$c_x$$$ be increased by $$$1$$$ (and the processing method for $$$d$$$ is the same). If $$$c_x < c_{x+1}$$$, then after the modification $$$c_x \leq c_{x+1}$$$, which would be fine. Otherwise, we can modify the array $$$c$$$ in the form of a single round of "Insertion Sort": We continuously swap $$$c_x$$$ and $$$c_{x+1}$$$, $$$x \gets x + 1$$$, until $$$c_x < c_{x+1}$$$ (or $$$x = n$$$), and thus the array remains sorted after the increment.
In fact, the swap operation does nothing in the above process: in these cases, $$$c_x = c_{x+1}$$$ holds! So we can just set $$$x'$$$ as the maximum $$$k$$$ such that $$$c_k = c_x$$$, and then increase $$$c_{x'}$$$ by $$$1$$$, after which $$$c$$$ is still sorted. The $$$k$$$ can be found with a naive binary search, so the problem is solved in $$$\mathcal O(n\log n + q(\log p + \log n))$$$ per test case.
#include <bits/stdc++.h>
constexpr int MOD = 998244353;
int qpow(int a, int x = MOD - 2) {
int res = 1;
for (; x; x >>= 1, a = 1ll * a * a % MOD) if (x & 1) res = 1ll * res * a % MOD;
return res;
}
#define MAXN 200001
int a[MAXN], b[MAXN], c[MAXN], d[MAXN];
void solve() {
int n, q, res = 1; std::cin >> n >> q;
for (int i = 1; i <= n; ++i) std::cin >> a[i], c[i] = a[i];
for (int i = 1; i <= n; ++i) std::cin >> b[i], d[i] = b[i];
std::sort(c + 1, c + n + 1), std::sort(d + 1, d + n + 1);
for (int i = 1; i <= n; ++i) res = 1ll * res * std::min(c[i], d[i]) % MOD;
std::cout << res << " \n"[q == 0];
for (int i = 1, op, x; i <= q; ++i) {
std::cin >> op >> x;
if (op == 1) {
int p = std::upper_bound(c + 1, c + n + 1, a[x]) - c - 1;
if (c[p] < d[p]) res = 1ll * res * qpow(c[p]) % MOD * (c[p] + 1) % MOD;
++a[x], ++c[p];
} else {
int p = std::upper_bound(d + 1, d + n + 1, b[x]) - d - 1;
if (d[p] < c[p]) res = 1ll * res * qpow(d[p]) % MOD * (d[p] + 1) % MOD;
++b[x], ++d[p];
}
std::cout << res << " \n"[i == q];
}
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr), std::cout.tie(nullptr);
int t; std::cin >> t; while (t--) solve(); return 0;
}
2053E - Resourceful Caterpillar Sequence
Suppose somebody wins. In which round does he or she win?
A player can always undo what his opponent did in the previous turn.
Can you find the necessary and sufficient condition for $$$(p, q)$$$ to be a caterpillar that makes Aron win?
Denote Nora's first move as round $$$1$$$, Aron's first move as round $$$2$$$, and so on. Suppose a player does not have a winning strategy in the $$$k$$$-th round, but he or she has a winning strategy in the $$$(k + 2)$$$-th round — it can be shown impossible because the other player can always withdraw the last move of another player so that the status is the same as it was before the $$$k$$$-th round.
Therefore: if a player wins in the $$$k$$$-th round, we claim that $$$k \leq 2$$$.
Given $$$p, q$$$, let's determine who will eventually win the game.
- If both $$$p$$$ and $$$q$$$ are leaves, the result is a tie.
- If $$$p$$$ is a leaf while $$$q$$$ is not, Nora wins.
- If $$$q$$$ is a leaf while $$$p$$$ is not, Aron wins.
- If neither $$$p$$$ nor $$$q$$$ is a leaf:
- Can $$$k = 1$$$? Nora wins if and only if $$$p$$$ is adjacent to a leaf.
- Can $$$k = 2$$$? Aron wins if and only if $$$p$$$ is not adjacent to a leaf, and $$$f(p, q)$$$ is adjacent to a leaf.
- Otherwise, the result is a tie.
The counting part can also be solved easily in $$$\mathcal O(n)$$$. Denote $$$c$$$ as the number of leaves. The initial answer would be $$$c \cdot (n - c)$$$, considering the third case. For the fourth case, we can enumerate $$$m = f(p, q)$$$, which is adjacent to at least one leaf. Given $$$m$$$, $$$q$$$ must be a non-leaf neighbor of $$$m$$$, and let the number of different $$$q$$$ be $$$k$$$. For each of the potential $$$p$$$, which is a non-leaf node whose neighbors are all non-leaf nodes too, it is computed exactly $$$k - 1$$$ times for all the $$$k$$$ candidates of $$$q$$$ (since $$$m$$$ must be on the simple path from $$$p$$$ to $$$q$$$), so the extra contributions are easy to calculate. (If you do not think that much, you can use some simple DP, which I will not elaborate here.)
#include <bits/stdc++.h>
#define MAXN 200001
std::vector<int> g[MAXN];
inline int deg(int u) { return g[u].size(); }
int d[MAXN];
void solve() {
int n; std::cin >> n; long long ans = 0;
for (int i = 1, u, v; i < n; ++i) {
std::cin >> u >> v;
g[u].push_back(v), g[v].push_back(u);
}
int c1 = 0, c2 = 0;
for (int i = 1; i <= n; ++i) c1 += (deg(i) == 1);
ans += 1ll * c1 * (n - c1);
for (int i = 1; i <= n; ++i) if (deg(i) > 1) {
for (int v : g[i]) d[i] += (deg(v) > 1);
c2 += (d[i] == deg(i));
}
for (int m = 1; m <= n; ++m) if (deg(m) > 1 && d[m] != deg(m))
ans += 1ll * c2 * (d[m] - 1);
std::cout << ans << '\n';
for (int i = 1; i <= n; ++i)
(std::vector<int>()).swap(g[i]), d[i] = 0;
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr), std::cout.tie(nullptr);
int t; std::cin >> t; while (t--) solve(); return 0;
}
2053F - Earnest Matrix Complement
Special thanks to LMydd0225 for implementing a correct MCS ahead of me, and Error_Yuan for generating the test data for this problem.
What are we going to fill into the matrix? In other words, is there any relationship between the filed numbers?
Try to come up with a naive DP solution that works in large time complexity, such as $$$\mathcal O(nk^2)$$$.
For many different numbers between two consecutive rows, however, the transition is almost the same.
If $$$x' = \max(a, x + b)$$$ and $$$x'' = \max(c, x' + d)$$$, then $$$x'' = \max(\max(a + d, c), x + b + d)$$$.
Conclusion: For each row, an optimal solution exists, such that the newly filled-in numbers are the same.
- Proof: Consider fixing the rows $$$i - 1$$$ and $$$i + 1$$$, and observe all the newly filled-in numbers at row $$$i$$$. Then a new number $$$u$$$ brings a contribution of $$$c_{u, i-1} + c_{u, i+1}$$$, and it is clear that there exists a scheme that takes the maximum value such that all the $$$u$$$ filled in are equal. Adjusting for each row leads to the above conclusion.
Consider dp. Let $$$f_{i,j}$$$ denote the maximum contribution that can be achieved between the first $$$i$$$ rows (ignoring the initial contribution) when the empty elements in the $$$i$$$-th row are filled with $$$j$$$. Let $$$c_i$$$ be the number of $$$-1$$$ numbers in the $$$i$$$-th row, and $$$d_{i,j}$$$ denote the number of elements $$$j$$$ in the $$$i$$$-th row initially.
The transfer should be as follows:
In addition to being able to optimize the above transition to $$$\mathcal O(nk)$$$, the present problem in a matrix has a good property. Specifically, for the same $$$i$$$, there are only $$$\mathcal O(m)$$$ values of $$$j$$$ such that $$$d_{i,j} \neq 0$$$!
If $$$d_{i,j} = 0$$$ and $$$d_{i-1, j} = 0$$$, the original transfer can be viewed as
This can be seen as a global modification in the form of $$$x \gets \max(a, x + b)$$$. The tags are composable in $$$\mathcal O(1)$$$; Otherwise, we can brutely update the new $$$dp_j$$$ for $$$\mathcal O(m)$$$ positions.
Therefore, this problem is solved in $$$\mathcal O(nm)$$$. We decided to let every segment tree solution pass comfortably, so that we set small constraints and large TL.
Bonus Hint for implementation: always use $$$\max(a, dp_j + b)$$$ to get the real value.
#include <bits/stdc++.h>
namespace FastIO {
char buf[1 << 21], *p1 = buf, *p2 = buf;
#define getchar() (p1 == p2 && (p1 = buf, p2 = (p1 + fread(buf, 1, 1 << 21, stdin))) == p1 ? EOF : *p1++)
template <typename T> inline T read() { T x = 0, w = 0; char ch = getchar(); while (ch < '0' || ch > '9') w |= (ch == '-'), ch = getchar(); while ('0' <= ch && ch <= '9') x = x * 10 + (ch ^ '0'), ch = getchar(); return w ? -x : x; }
template <typename T> inline void write(T x) { if (!x) return; write<T>(x / 10), putchar((x % 10) ^ '0'); }
template <typename T> inline void print(T x) { if (x > 0) write<T>(x); else if (x < 0) putchar('-'), write<T>(-x); else putchar('0'); }
template <typename T> inline void print(T x, char en) { print<T>(x), putchar(en); }
#undef getchar
}; using namespace FastIO;
using ll = long long;
void solve() {
int n = read<int>(), m = read<int>(), k = read<int>(); ll cntP = 0, cntQ = 0;
std::vector<int> vep(m), veq(m), cntp(k + 1), cntq(k + 1), vis(k + 1);
std::vector<ll> dp(k + 1); ll a = 0, b = 0, v = 0, ext = 0; // max(a, x + b).
cntp[0] = cntq[0] = m;
auto get = [&](int x) -> int { return (~x) ? x : 0; };
auto read_q = [&]() -> void {
for (int i = 0; i < m; ++i) --cntq[get(veq[i])];
for (int i = 0; i < m; ++i) ++cntq[get(veq[i] = read<int>())];
cntQ = cntq[0];
};
auto roll = [&]() -> void { std::swap(vep, veq), std::swap(cntp, cntq), std::swap(cntP, cntQ); };
auto chkmax = [&](ll &a, ll b) -> void { a = std::max(a, b); };
read_q(), roll();
for (int i = 2; i <= n; ++i) {
read_q();
ll max_dp = std::max(a, v + b);
for (int k : vep) if (~k) chkmax(max_dp, std::max(a, dp[k] + b) + cntP * cntq[k]);
for (int k : veq) if (~k) chkmax(max_dp, std::max(a, dp[k] + b) + cntP * cntq[k]);
for (int k : vep) if ((~k) && vis[k] != i) {
vis[k] = i, ext += 1ll * cntp[k] * cntq[k];
dp[k] = std::max(a, dp[k] + b) + cntP * cntq[k] + cntQ * cntp[k] - b;
chkmax(dp[k], max_dp + cntp[k] * cntQ - b - cntP * cntQ);
chkmax(v, dp[k]);
} for (int k : veq) if ((~k) && vis[k] != i) {
vis[k] = i;
dp[k] = std::max(a, dp[k] + b) + cntP * cntq[k] + cntQ * cntp[k] - b;
chkmax(dp[k], max_dp + cntp[k] * cntQ - b - cntP * cntQ);
chkmax(v, dp[k]);
} a = std::max(max_dp, a + cntP * cntQ), b += cntP * cntQ;
roll();
} print<ll>(std::max(a, v + b) + ext, '\n');
}
int main() { int T = read<int>(); while (T--) solve(); return 0; }
Special thanks to LMydd0225 for generating the test data for this problem, and TheScrasse for providing an alternative solution.
And thanks to Caylex for implementing a really correct MCS and rewriting the editorial, and crazy_sea for offering a suggestion.
(If we do not have to be deterministic) We do not need any hard string algorithm.
In what cases won't greed work? Why?
Is your brute forces actually faster (maybe you can explain it by harmonic series)?
Let's call the prefix $$$s_1$$$ the short string and the suffix $$$s_2$$$ the long string. If $$$\lvert s_1\rvert\gt \lvert s_2\rvert$$$, swapping the order doesn't affect the answer.
Consider a greedy approach. We first match a few short strings until we can't match anymore. If we can't match, we try discarding a few short strings and placing one long string. We enumerate how many short strings to discard. Find the first position where we can place a long string. We call this placing once a "matching process." The starting position of each "matching process" is the next position after the previous "matching process."
However, this approach has a flaw. Below, I will explain the situation where this flaw occurs.
It's not difficult to view the long string as several short strings concatenated with a "tail" at the end.
Why only find the first position? Why wouldn't it be better to backtrack and discard a few more $$$s_1$$$'s before placing the long string?
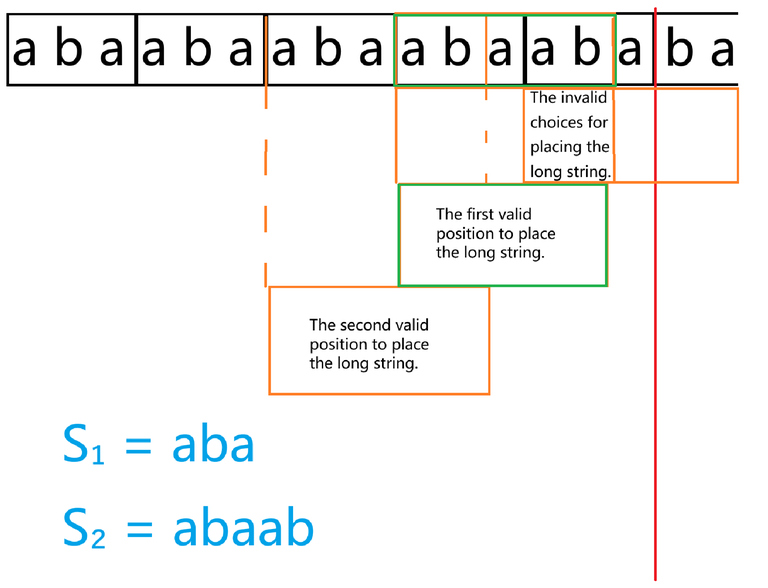
The diagram above is an example. The red line indicates the cutoff position for matching $$$s_1$$$. The three orange boxes represent the possible choices for attempting to match the long string.
The last one is invalid, so skip it. Replace it with the "The first valid position to place the long string." box. This box is correct.
The difference between choosing the second box and the first box is that when we end the matching and proceed to the next round, the content we need to match is that a suffix of $$$s_1$$$ has been moved to the beginning of $s_1$。
As shown in the diagram.
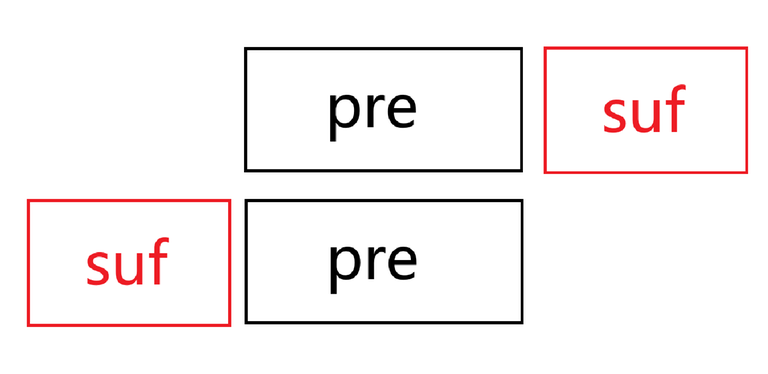
The alignment results in the following diagram.
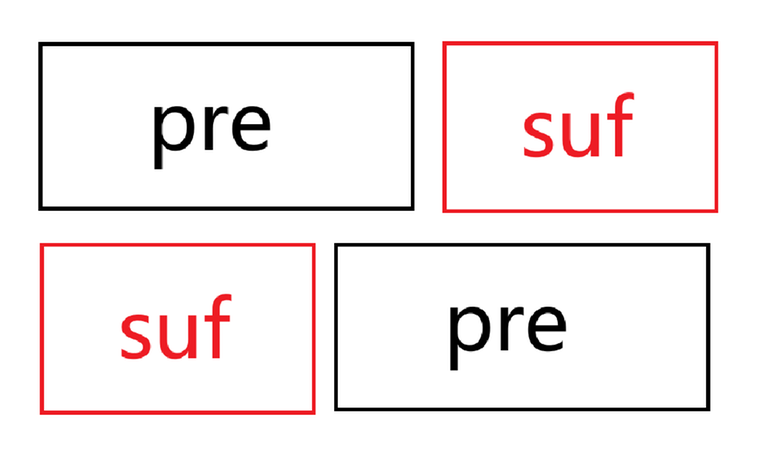
In the diagram, the case where $$$\lvert pre\rvert \gt \lvert suf\rvert$$$ is shown. The other case follows similarly.
$$$pre+suf=suf+pre$$$, and as can be seen from the diagram, here $$$pre+suf$$$ needs to be "misaligned but equal." This means that $$$s_1$$$ must have a periodic cycle, and the "tail" must also be able to be formed through this cycle. Additionally, the $$$\lvert s_1 \rvert$$$ characters at the beginning of $$$s_2$$$ must still be able to be formed by the periodic cycle.
In summary, it is equivalent to $$$s_1$$$ and $$$s_2$$$ having a common periodic cycle.
In other words, backtracking twice can lead to a solution, but backtracking once may not always work. It is necessary for $$$s_1$$$ and $$$s_2$$$ to have a common periodic cycle.
Having a common periodic cycle is too specific. First, the common periodic cycle of these two strings must indeed be the periodic cycle of string $$$s$$$. By finding this cycle in advance, it essentially becomes a problem of solving an equation. Let $$$a=\lvert s_1\rvert $$$ and $$$b=\lvert s_2\rvert$$$, and we need to check whether there are non-negative integer solutions $$$x$$$ and $$$y$$$ that satisfy the equation $$$xa+yb=\lvert s \rvert$$$.
This equation-solving part is just for show. We enumerate $$$y$$$, and for each value of $$$y$$$, we compute the enumeration $$$\mathcal O\left(\frac{m}{n}\right)$$$ times. At most, we do this $$$n$$$ times, so the overall complexity is $$$\mathcal O(m)$$$.
If we directly implement this, the worst-case complexity is related to the harmonic series. Consider a case like $$$s_1 = \texttt{a}, s_2 = \texttt{aaaaaaaab}$$$, and $$$t = \texttt{aaaaaaaaaaaaaaaaaaaaaaaaab}$$$. In this case, we would need to attempt $$$\mathcal O\left(\frac{m}{\lvert s_1\rvert }\right)$$$ steps to finish matching the short string. Each time we backtrack, it requires at most $$$\mathcal O\left(\frac{m}{\lvert s_2\rvert }\right)$$$ steps, and each of those takes $$$\mathcal O\left(\frac{\lvert s_2\rvert }{\lvert s_1\rvert }\right)$$$.
Thanks to orzdevinwang and crazy_sea for pointing out it!
Yes, this problem can indeed be solved in linear time.
First, let the prefix of the long string contain $$$c$$$ short strings. Then, the first "valid position to place the long string" we backtrack to can only be obtained by either backtracking $$$c$$$ short strings or $$$c+1$$$ short strings.
This is easy to understand. Backtracking $$$c$$$ short strings means considering the prefix of the long string, then adding the "tail" of the long string. Backtracking $$$c + 1$$$ short strings only happens when the "tail" part of the long string is a prefix of the short string. For example, the hack in the CF comment section:
https://codeforces.me/blog/entry/136455?#comment-1234262
1
8 8
abaabaab
abaababa
The correct output should be:
0010000
When $$$k = 3$$$, $$$s_1 = \texttt{aba}$$$, $$$s_2 = \texttt{abaab}$$$, we first filled in 2 short strings, but if we backtrack $$$c = 1$$$ short string, it will be judged as unsolvable. This is how the error in std occurs. This situation only arises when the "tail" part of $$$s_2$$$ is a prefix of $$$s_1$$$.
So, each time we calculate, we first use binary search to find this $$$c$$$, and the complexity is $$$\mathcal O\left(\sum\limits_{i=1}^n\log(\frac n i)\right)=\mathcal O(n)$$$. After that, backtracking only requires two checks. The backtracking process becomes linear.
Next, let's accelerate the process of filling in short strings. The hack for brute-force filling has already been given above. If we directly use the method that everyone initially thought was correct, which is the "binary search for the number of short string occurrences" method, Then it can be accelerated by this set of hacks to achieve a $$$\log$$$ complexity.
1
2 5000000
ab
abababab....abababab
crazy_sea points out an alternative solution.
Similar to block division, let $$$B = \frac{n}{\lvert s_1\rvert}$$$. We first try to match $$$B$$$ occurrences of $$$s_1$$$, meaning that each match can move forward by $$$n$$$ positions. After that, the remaining part will not exceed $$$B$$$ occurrences, and we binary search to find how many are left. For the part where we moved forward by $$$B$$$ occurrences, we can backtrack at most once, and then the binary search will take $$$\mathcal O(\log B)$$$. Each time, we can at least fill in $$$\lvert s_2\rvert $$$ occurrences. The time complexity for calculating the answer becomes $$$\mathcal O\left(\frac{m}{\lvert s_2\rvert }\log B\right)$$$, and the total complexity, due to $$$\mathcal O\left(\sum\limits_{i=1}^n \log(\frac{n}{i})\right) = \mathcal O(n)$$$, is $$$\mathcal O(m)$$$.
Thus, the problem is solved in linear time.
During testing, we found that jqdai0815's solution is actually more violent than we thought (We have also received something similar in contest).
He specially handled the case in which $$$X$$$ and $$$T$$$ share a common shortest period, and for the rest $$$i$$$, he just used two queues to optimize the BFS progress (actually changing it to std::priority_queue<int> or similar also works), and it passed just seeming to have a larger constant time complexity.
I'm curious if anybody can (hack it or) prove that it is correct. Thanks in advance!
This is written by Caylex.
#include <bits/stdc++.h>
using namespace std;
template <int P>
class mod_int
{
using Z = mod_int;
private:
static int mo(int x) { return x < 0 ? x + P : x; }
public:
int x;
int val() const { return x; }
mod_int() : x(0) {}
template <class T>
mod_int(const T &x_) : x(x_ >= 0 && x_ < P ? static_cast<int>(x_) : mo(static_cast<int>(x_ % P))) {}
bool operator==(const Z &rhs) const { return x == rhs.x; }
bool operator!=(const Z &rhs) const { return x != rhs.x; }
Z operator-() const { return Z(x ? P - x : 0); }
Z pow(long long k) const
{
Z res = 1, t = *this;
while (k)
{
if (k & 1)
res *= t;
if (k >>= 1)
t *= t;
}
return res;
}
Z &operator++()
{
x < P - 1 ? ++x : x = 0;
return *this;
}
Z &operator--()
{
x ? --x : x = P - 1;
return *this;
}
Z operator++(int)
{
Z ret = x;
x < P - 1 ? ++x : x = 0;
return ret;
}
Z operator--(int)
{
Z ret = x;
x ? --x : x = P - 1;
return ret;
}
Z inv() const { return pow(P - 2); }
Z &operator+=(const Z &rhs)
{
(x += rhs.x) >= P && (x -= P);
return *this;
}
Z &operator-=(const Z &rhs)
{
(x -= rhs.x) < 0 && (x += P);
return *this;
}
Z operator-() { return -x; }
Z &operator*=(const Z &rhs)
{
x = 1ULL * x * rhs.x % P;
return *this;
}
Z &operator/=(const Z &rhs) { return *this *= rhs.inv(); }
#define setO(T, o) \
friend T operator o(const Z &lhs, const Z &rhs) \
{ \
Z res = lhs; \
return res o## = rhs; \
}
setO(Z, +) setO(Z, -) setO(Z, *) setO(Z, /)
#undef setO
friend istream &
operator>>(istream &is, mod_int &x)
{
long long tmp;
is >> tmp;
x = tmp;
return is;
}
friend ostream &operator<<(ostream &os, const mod_int &x)
{
os << x.val();
return os;
}
};
typedef long long ll;
typedef unsigned long long ull;
mt19937 rnd(chrono::system_clock::now().time_since_epoch().count());
constexpr int p = 993244853;
using Hash = mod_int<p>;
// using Hash = ull;
const Hash base = rnd() % 20091119 + 30;
string s, t;
Hash st;
int mnlen;
Hash S[5000020];
Hash T[5000020];
Hash pw[5000020];
inline Hash SUM(const int l, const int r, const Hash *s) { return s[r] - s[l - 1] * pw[r - l + 1]; }
int n, m;
inline bool check(const int l, const int r, const Hash x, const int len, const Hash *S) { return r - l + 1 >= len && SUM(l, l + len - 1, S) == x && SUM(l, r - len, S) == SUM(l + len, r, S); }
inline bool calc(const int L1, const int R1, const int L2, const int R2, const int l1, const int l2)
{
if (mnlen && check(L1, R1, st, mnlen, S) && check(L2, R2, st, mnlen, S))
{
if (check(1, m, st, mnlen, T))
{
for (int i = 0; i <= m; i += l2)
{
if (!((m - i) % l1))
return 1;
}
return 0;
}
}
const Hash s1 = SUM(L1, R1, S);
const Hash s2 = SUM(L2, R2, S);
// int l = 1, r = l2 / l1, okcnt = 0;
// while (l <= r)
// {
// int mid = l + r >> 1;
// if (check(L2, L2 + mid * l1 - 1, s1, l1, S))
// l = (okcnt = mid) + 1;
// else
// r = mid - 1;
// }
int ed = 0;
while (ed <= m)
{
int L = 1, R = (m - ed) / l1, cnt = 0;
while (L <= R)
{
int mid = L + R >> 1;
if (check(ed + 1, ed + mid * l1, s1, l1, T))
L = (cnt = mid) + 1;
else
R = mid - 1;
}
if (ed + cnt * l1 + 1 > m)
return 1;
// bool found = 0;
// int st = ed + (cnt - okcnt) * l1 + 1;
// if (st > ed && st + l2 - 1 <= m && SUM(st, st + l2 - 1, T) == s2)
// {
// ed = st + l2 - 1;
// found = 1;
// }
// if (!found)
// return 0;
bool found = 0;
for (int st = ed + cnt * l1 + 1; st > ed; st -= l1)
{
if (st + l2 - 1 <= m && SUM(st, st + l2 - 1, T) == s2)
{
ed = st + l2 - 1;
found = 1;
break;
}
}
if (!found)
return 0;
}
return 1;
}
void solve()
{
// build();
mnlen = 0;
cin >> n >> m >> s >> t;
s = ' ' + s;
t = ' ' + t;
for (int i = 1; i <= n; i++)
S[i] = S[i - 1] * base + Hash(s[i] - 'a' + 1);
for (int i = 1; i <= m; i++)
T[i] = T[i - 1] * base + Hash(t[i] - 'a' + 1);
for (int i = 1; i <= n; i++)
{
if (n % i == 0 && check(1, n, S[i], i, S))
{
st = S[i];
mnlen = i;
break;
}
}
for (int i = 1; i < n; i++)
putchar('0' ^ (i <= n - i ? calc(1, i, i + 1, n, i, n - i) : calc(i + 1, n, 1, i, n - i, i)));
putchar('\n');
}
int main()
{
pw[0] = Hash(1);
for (int i = 1; i <= 5'000'000; i++)
pw[i] = pw[i - 1] * base;
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t;
cin >> t;
while (t--)
solve();
return 0;
}
This is written by Caylex.
#include <bits/stdc++.h>
using namespace std;
template <int P>
class mod_int
{
using Z = mod_int;
private:
static int mo(int x) { return x < 0 ? x + P : x; }
public:
int x;
int val() const { return x; }
mod_int() : x(0) {}
template <class T>
mod_int(const T &x_) : x(x_ >= 0 && x_ < P ? static_cast<int>(x_) : mo(static_cast<int>(x_ % P))) {}
bool operator==(const Z &rhs) const { return x == rhs.x; }
bool operator!=(const Z &rhs) const { return x != rhs.x; }
Z operator-() const { return Z(x ? P - x : 0); }
Z pow(long long k) const
{
Z res = 1, t = *this;
while (k)
{
if (k & 1)
res *= t;
if (k >>= 1)
t *= t;
}
return res;
}
Z &operator++()
{
x < P - 1 ? ++x : x = 0;
return *this;
}
Z &operator--()
{
x ? --x : x = P - 1;
return *this;
}
Z operator++(int)
{
Z ret = x;
x < P - 1 ? ++x : x = 0;
return ret;
}
Z operator--(int)
{
Z ret = x;
x ? --x : x = P - 1;
return ret;
}
Z inv() const { return pow(P - 2); }
Z &operator+=(const Z &rhs)
{
(x += rhs.x) >= P && (x -= P);
return *this;
}
Z &operator-=(const Z &rhs)
{
(x -= rhs.x) < 0 && (x += P);
return *this;
}
Z operator-() { return -x; }
Z &operator*=(const Z &rhs)
{
x = 1ULL * x * rhs.x % P;
return *this;
}
Z &operator/=(const Z &rhs) { return *this *= rhs.inv(); }
#define setO(T, o) \
friend T operator o(const Z &lhs, const Z &rhs) \
{ \
Z res = lhs; \
return res o## = rhs; \
}
setO(Z, +) setO(Z, -) setO(Z, *) setO(Z, /)
#undef setO
friend istream &
operator>>(istream &is, mod_int &x)
{
long long tmp;
is >> tmp;
x = tmp;
return is;
}
friend ostream &operator<<(ostream &os, const mod_int &x)
{
os << x.val();
return os;
}
};
typedef long long ll;
typedef unsigned long long ull;
mt19937 rnd(chrono::system_clock::now().time_since_epoch().count());
constexpr int p = 993244853;
using Hash = mod_int<p>;
// using Hash = ull;
const Hash base = rnd() % 20091119 + 30;
string s, t;
Hash st;
int mnlen;
Hash S[5000020];
Hash T[5000020];
Hash pw[5000020];
// int doit;
inline Hash SUM(const int l, const int r, const Hash *s) { return s[r] - s[l - 1] * pw[r - l + 1]; }
int n, m;
inline bool check(const int l, const int r, const Hash x, const int len, const Hash *S)
{
// doit++;
return r - l + 1 >= len && SUM(l, l + len - 1, S) == x && SUM(l, r - len, S) == SUM(l + len, r, S);
}
inline bool calc(const int L1, const int R1, const int L2, const int R2, const int l1, const int l2)
{
if (mnlen && check(L1, R1, st, mnlen, S) && check(L2, R2, st, mnlen, S))
{
if (check(1, m, st, mnlen, T))
{
for (int i = 0; i <= m; i += l2)
{
if (!((m - i) % l1))
return 1;
}
return 0;
}
}
const Hash s1 = SUM(L1, R1, S);
const Hash s2 = SUM(L2, R2, S);
int l = 1, r = l2 / l1, okcnt = 0;
while (l <= r)
{
int mid = l + r >> 1;
if (check(L2, L2 + mid * l1 - 1, s1, l1, S))
l = (okcnt = mid) + 1;
else
r = mid - 1;
}
const int tt = (n / l1);
int ed = 0;
while (ed <= m)
{
int L = 1, R = (m - ed) / l1, cnt = 0;
int tcnt = 0;
while (tcnt + tt <= R && check(ed + 1, ed + (tcnt + tt) * l1, s1, l1, T))
tcnt += tt;
L = max(L, tcnt);
R = min(R, tcnt + tt - 1);
// cerr << ed << ' ' << L << ' ' << R << '\n';
while (L <= R)
{
int mid = L + R >> 1;
if (check(ed + 1, ed + mid * l1, s1, l1, T))
L = (cnt = mid) + 1;
else
R = mid - 1;
}
if (ed + cnt * l1 + 1 > m)
return 1;
// int st = ed + (cnt - okcnt) * l1 + 1;
// if (st > ed && st + l2 - 1 <= m && SUM(st, st + l2 - 1, T) == s2)
// {
// ed = st + l2 - 1;
// continue;
// }
// return 0;
bool found = 0;
for (int st = ed + (cnt - okcnt) * l1 + 1, cnt = 1; cnt <= 2 && st > ed; st -= l1, cnt++)
{
if (st + l2 - 1 <= m && SUM(st, st + l2 - 1, T) == s2)
{
ed = st + l2 - 1;
found = 1;
break;
}
}
if (!found)
return 0;
}
return 1;
}
void solve()
{
// build();
mnlen = 0;
cin >> n >> m >> s >> t;
s = ' ' + s;
t = ' ' + t;
for (int i = 1; i <= n; i++)
S[i] = S[i - 1] * base + Hash(s[i] - 'a' + 1);
for (int i = 1; i <= m; i++)
T[i] = T[i - 1] * base + Hash(t[i] - 'a' + 1);
for (int i = 1; i <= n; i++)
{
if (n % i == 0 && check(1, n, S[i], i, S))
{
st = S[i];
mnlen = i;
break;
}
}
for (int i = 1; i < n; i++)
putchar('0' ^ (i <= n - i ? calc(1, i, i + 1, n, i, n - i) : calc(i + 1, n, 1, i, n - i, i)));
putchar('\n');
// cerr << doit << '\n';
}
int main()
{
// freopen("out.txt", "r", stdin);
pw[0] = Hash(1);
for (int i = 1; i <= 5'000'000; i++)
pw[i] = pw[i - 1] * base;
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t;
cin >> t;
while (t--)
solve();
// cerr << fixed << setprecision(10) << 1.0 * clock() / CLOCKS_PER_SEC << '\n';
return 0;
}
2053H - Delicate Anti-monotonous Operations
Special thanks to LMydd0225 and N_z__ for developing this problem.
What if $$$w = 2$$$? Is it optimal to increase $$$\sum\limits_{i=0}^n [a_i \neq a_{i+1}]$$$ (suppose $$$a_0 = a_{n+1} = 2$$$)?
If $$$w \geq 3$$$, what's the answer to the first question?
If $$$a_i = a_{i+1}$$$, after the operation we can obtain $$$a_{i-1} = a_i$$$ or $$$a_{i+1} = a_{i+2}$$$ (and possibly, both).
Try to think of the whole process reversedly. If $$$w \geq 3$$$, $$$1 \leq a_i \leq w - 1$$$, can you solve the problem?
How many extra operations are required for each $$$1 \leq i \leq n$$$ if $$$a_i = w$$$, in the above scheme you use for $$$a_i \leq w - 1$$$?
Read the Hints.
- $$$w = 2$$$
After any operation, $$$k = \sum\limits_{i=0}^n [a_i \neq a_{i+1}]$$$ won't decrease (suppose $$$a_0 = a_{n+1} = 2$$$). For a fixed $$$k$$$, the maximal $$$\sum a_i = 2n - \frac{1}{2}k$$$ and can be reached by each time turning a $$$[2, 1, 1]$$$ into $$$[2, 2, 1]$$$ (or symmetrically, $$$[1, 1, 2] \rightarrow [1, 2, 2]$$$.
- $$$w \geq 3$$$
- No initial operations can be conducted, or $$$\min(a_i) = w$$$
This case is trivial.
- $$$w \geq 3$$$
- Some initial operations can be conducted
We claim that the answer to the first question is $$$nw - 1$$$. For the second question, let's study some rather easier cases below.
- $$$w \geq 3$$$
- Some initial operations can be conducted
- $$$a_i \neq w$$$
- Some initial operations can be conducted
We pretend that the final sequence is $$$[w, w, \dots, w, (w-1), w, w, \dots, w]$$$, then since $$$(a_i, a_{i+1})$$$ must be different after the operation, the last operation can only occur on $$$[w, (w-1)]$$$ (or $$$[(w-1), w]$$$). And since initially $$$a_i \neq w$$$, each position must have been operated on at least once.
This gives us states such as $$$[w, \dots, w, x, x, w, \dots, w]$$$, $$$[w, \dots, w, y, y, x, w, \dots, w]$$$, etc. To the leftmost positions, we get $$$a_1 = a_2$$$ (essentially based on Hint 3). Also, we get ...... $$$a_{n-1} = a_n$$$? This is if and only if the initial $$$[w, (w - 1)]$$$ is neither at the beginning nor at the end. If the initial $$$[w, (w - 1)]$$$ is at the beginning, we only need $$$a_{n-1} = a_n$$$ to achieve the goal, and symmetrically the same. Less is more. Obviously, we only need to satisfy either $$$a_1 = a_2$$$ or $$$a_{n-1} = a_n$$$, and then use $$$n - 1$$$ more operations to reach the target situation.
How do we get to $$$a_1 = a_2$$$ (symmetrically the same)? Based on Hint 3, we find the smallest $$$x$$$ that satisfies $$$a_x = a_{x+1}$$$, and then follow the example above, again using $$$x - 1$$$ operations to conduct the equality sign to $$$a_1 = a_2$$$.
Lemma 1: We can never choose an index $$$a_i = w$$$, fix it (i.e. avoid changing $$$a_i$$$ in the following operations), and then use some operations to reach $$$\sum a_i = nw - 1$$$ unless $$$[a_1, \ldots, a_i] = [w, \ldots, w]$$$ or $$$[a_i, \ldots, a_n] = [w, \ldots, w]$$$.
Proof: If not so, the array is split into two parts: $$$[a_1, \ldots, a_{i-1}]$$$ and $$$[a_{i+1}, \ldots, a_n]$$$. We have: after some operations, the maximum $$$\sum a_i$$$ we can get for each part are respectively $$$(i-1)w - 1, (n-i)w - 1$$$, and add them up and we get $$$nw - 2$$$, which is less than $$$nw - 1$$$, so it's never optimal.
Lemma 2: Look at the final array $$$a$$$, consisting of $$$n - 1$$$ element $$$w$$$ and $$$1$$$ element $$$(w - 1)$$$. Obtain an array $$$a'$$$ by keeping the elements with the value of $$$w$$$. Denote $$$t_i$$$ as the last round in which $$${a'}_i$$$ was changed to $$$w$$$ (and then become fixed). Then, there exists some $$$k$$$ such that $$$t_1 < t_2 < \dots < t_k > t_{k+1} > \dots > t_{n-1}$$$.
Proof: This follows from Lemma 1.
According to Lemma 2, we can see the pattern that we used above is optimal.
- $$$w \geq 3$$$
- Some initial operations can be conducted
- $$$a_1 \neq w, a_n \neq w$$$
- Some initial operations can be conducted
Basically, the idea remains to reach $$$a_1 = a_2$$$ in the same way first (symmetrically the same), and then to extend to all positions. However, at this point, in the second stage, some problems may arise as follows:
- $$$[\dots \underline{a_k}\ a_{k+1}\ w\ a_{k+3} \dots]$$$
- $$$[\dots \underline{\color{red}{a_{k+1}}\ a_{k+1}}\ w\ a_{k+3} \dots]$$$
- $$$[\dots \color{red}s\ \underline{\color{red}w\ w}\ a_{k+3} \dots]$$$
- $$$[\dots \color{red}{\underline{s\ s}}\ t\ a_{k+3} \dots]$$$
- $$$[\dots \color{red}w\ \underline{\color{red}t\ t}\ a_{k+3} \dots]$$$
- $$$[\dots \color{red}{w\ w}\ \underline{\color{red}{a_{k+3}}\ a_{k+3}} \dots]$$$
In which $$$s, t, w$$$ are three distinct integers in the range $$$[1, w]$$$ (This also explains why we need to specially deal with the $$$w = 2$$$ case). Since we cannot fix $$$a_{k+2} = w$$$ at the beginning (refer to the "Why is it optimal?" spoiler above), we have to first change $$$a_{k+2}$$$ into something not equal to $$$w$$$, and that cost at least $$$2$$$ extra operations, which is shown here.
Do we always need $$$2$$$ extra operations? One may note that if $$$a_i = a_{i+1} = w$$$, in which the two elements are both in the way of expansion, we can only use $$$1$$$ operation to vanish their existence. Formally, if there is a maximum continuous subsegment of $$$w$$$ in the way of expansion, let its length be $$$L$$$, then we will spend $$$\lceil \frac{L}{2} \rceil + [L = 1]$$$ extra operations.
Suppose in the first stage, we pick $$$a_x = a_{x+1}$$$ and keep operating on it until $$$a_1 = a_2$$$. Then after it, $$$\forall 3 \leq k \leq x + 1$$$, $$$a_k$$$ can be an arbitrary number which is different from the initial $$$a_{k-1}$$$, thus we can always force it to be $$$\neq w$$$.
In the above case, only elements $$$[a_{x+2}, \ldots, a_n]$$$ are considered 'in the way of expansion', and symmetrically the same.
- $$$w \geq 3$$$
- Some initial operations can be conducted
- No additional constraints
- Some initial operations can be conducted
It may come to you that if $$$a_1 = w$$$, we can ignore $$$a_1$$$; if $$$a_1 = a_2 = w$$$, we can ignore $$$a_2$$$. Symmetrically the same. And so on... Then we boil the problem down to the case above.
It is correct unless in some rare cases when we ignore all the prefixes and suffixes, there will be no remaining $$$a_i = a_{i+1}$$$; or if we pick any pair $$$a_i = a_{i+1}$$$ as the starting pair in the remaining array, it is not optimal compared to picking an $$$a_k = a_{k+1} = w (a_{k+2} \neq w)$$$ (symmetrically the same). So, we have to special handle the deleted prefix and suffix, once it has a length greater than $$$2$$$.
In summary, the problem can be solved in $$$\mathcal O(n)$$$.
#include <bits/stdc++.h>
#define MAXN 200005
int a[MAXN];
void solve() {
int N, w; scanf("%d%d", &N, &w);
for (int i = 1; i <= N; ++i) scanf("%d", a + i);
if (N == 1) return (void)printf("%d 0\n", a[1]);
if (*std::min_element(a + 1, a + N + 1) == w)
return (void)printf("%lld 0\n", 1ll * w * N);
if (w == 2) {
int ans = N * 2, pans = 0;
for (int i = 1, j = 1; i <= N; i = ++j) if (a[i] == 1) {
--ans; while (j < N && a[j + 1] == 1) ++j; pans += j - i;
}
return (void)printf("%d %d\n", ans, pans);
}
bool flag = true;
for (int i = 1; i < N; ++i) if (a[i] == a[i + 1]) flag = false;
if (flag) return (void)printf("%lld 0\n", std::accumulate(a + 1, a + N + 1, 0ll));
printf("%lld ", 1ll * w * N - 1);
if (std::accumulate(a + 1, a + N + 1, 0ll) == 1ll * w * N - 1) return (void)puts("0");
int ans = 0x3f3f3f3f, l = (a[1] == w ? 2 : 1), r = (a[N] == w ? N - 1 : N);
if ((a[1] == w && a[2] == w) || (a[N] == w && a[N - 1] == w)) {
int Lw = 0, Rw = N + 1;
while (a[Lw + 1] == w) ++Lw; while (a[Rw - 1] == w) --Rw;
int pans = Rw - Lw;
for (int i = Lw + 1, j = i; i < Rw; i = ++j) if (a[i] == w) {
while (j + 1 < Rw && a[j + 1] == w) ++j;
pans += (i == j ? 2 : ((j - i) >> 1) + 1);
}
ans = pans, l = Lw + 1, r = Rw - 1;
}
for (int d = 0; d < 2; std::reverse(a + l, a + r + 1), ++d)
for (int i = l - 1, pre = 0, len = 0; i + 2 <= r; ) {
if (a[i + 1] == a[i + 2])
ans = std::min(r - (i + 1) + r - l - 1 + pre - ((len == 1) && i + 2 < r && a[i + 3] != w ? 1 : 0), ans);
++i; if (a[i] == w) ++len, pre += (len == 1 ? 2 : len == 2 ? -1 : (len & 1)); else len = 0;
}
printf("%d\n", ans);
}
int main() { int T; scanf("%d", &T); while (T--) solve(); return 0; }
2053I1 - Affectionate Arrays (Easy Version)
What is the minimized LIS?
How do you prove that it is an achievable lower bound?
Go for a brute DP first.
We claim that the minimized LIS is $$$\sum a_i$$$. Let $$$p$$$ be $$$\sum a_i$$$.
Since it is required that $$$\operatorname{LIS}(b) = p$$$ while $$$\sum b_i = p$$$, we point out that it is equivalent to each of the prefix sums of the sequence being between $$$[0, p]$$$.
- Sufficiency: $$$\forall X \in [0, p], Y \in [0, p]$$$, $$$X - Y \leq p$$$. Also, we can pick $$$X = p, Y = 0$$$, so it can only be $$$= p$$$.
- Necessity: disproof. If a prefix sum is $$$< 0$$$, then choose the whole array except for this prefix; if a prefix sum is $$$> p$$$, then choose this prefix. Both derive a contradiction of the LIS being greater than $$$p$$$.
Consider dp. Let $$$f_{i,j}$$$ denote, after considering the first $$$i$$$ numbers, the minimum extra sequence length (i.e. the actual length minus $$$i$$$), when the current prefix sum is $$$j$$$. The initial states are $$$f_{0,j} = [j \neq 0]$$$. The transfer is simple too:
It is possible to optimize the transfer to $$$\mathcal O(np)$$$, since for each $$$j$$$, the contribution from at most one $$$k$$$ is special ($$$+0$$$). We can calculate the prefix and suffix $$$\min$$$ for $$$f_{i-1}$$$ and it will be fast to get the dp array in the new row. Then, let's focus on optimizing it to $$$\mathcal O(n)$$$.
We call the set of $$$0 \leq k \leq p$$$ satisfying $$$0 \leq k + a_i \leq p$$$ as the legal interval of $$$i$$$ (denoted as $$$L_i$$$).
It is concluded that the range of $$$f_{i, 0\dots p}$$$ is at most $$$1$$$, and this can be proven by considering the transfer to each of the $$$j$$$ with the $$$k \in L_i$$$ which has the least $$$f_{i-1, k}$$$. Let $$$v_i = \min_{0 \leq j \leq p}(f_{i, j})$$$. We also have: for those $$$j$$$ with $$$f_{i,j} = v_i$$$, they form a consecutive segment in the integer field. Let the segment be covering $$$[l_i, r_i]$$$.
Inductive proof. The essence of the transfer is that it shifts all the DP values $$$= v_{i-1}$$$ by $$$a_i$$$ unit length, and all the other numbers will be updated to $$$v_{i-1} + 1$$$. Then truncates the $$$j \in ((-\inf, 0) \cup (p, +\inf))$$$ part. The consecutive segment remains consecutive. Specially, if $$$[l_{i-1}, r_{i-1}] \cap L_i = \varnothing$$$, then $$$\min_{k \in L_i}(f_{i-1, k}) = v_{i-1} + 1$$$, hence we need to set $$$v_i = v_{i-1} + 1$$$, and $$$l_i, r_i$$$ as the range of $$$j = k + a_i$$$ in which $$$k \in L_i$$$. Otherwise, $$$v_i = v_{i-1}$$$, and $$$l_i, r_i$$$ can be calculated by shifting $$$l_{i-1}, r_{i-1}$$$ by $$$a_i$$$ unit length.
In fact, we only need to maintain three variables $$$l, r, v$$$ to represent the current consecutive segment and the current value field. Therefore, this problem can be easily solved in $$$\mathcal O(n)$$$.
#include <bits/stdc++.h>
namespace FastIO {
template <typename T> inline T read() { T x = 0, w = 0; char ch = getchar(); while (ch < '0' || ch > '9') w |= (ch == '-'), ch = getchar(); while ('0' <= ch && ch <= '9') x = x * 10 + (ch ^ '0'), ch = getchar(); return w ? -x : x; }
template <typename T> inline void write(T x) { if (!x) return; write<T>(x / 10), putchar((x % 10) ^ '0'); }
template <typename T> inline void print(T x) { if (x > 0) write<T>(x); else if (x < 0) putchar('-'), write<T>(-x); else putchar('0'); }
template <typename T> inline void print(T x, char en) { print<T>(x), putchar(en); }
}; using namespace FastIO;
#define MAXN 3000001
int a[MAXN];
void solve() {
int N = read<int>(); long long p = 0, l = 0, r = 0, v = 0;
for (int i = 1; i <= N; ++i) p += (a[i] = read<int>());
for (int i = 1; i <= N; ++i) if (a[i] >= 0) {
l += a[i], r = std::min(r + a[i], p);
if (l > r) ++v, l = a[i], r = p;
} else {
a[i] = -a[i];
r -= a[i], l = std::max(l - a[i], 0ll);
if (l > r) ++v, l = 0, r = p - a[i];
}
print<int>(v + N + (int)(r != p), '\n');
}
int main() { int T = read<int>(); while (T--) solve(); return 0; }
2053I2 - Affectionate Arrays (Hard Version)
Try insert numbers into spaces between the elements of $$$a$$$ (including the beginning and the end). Note that an array be can be formed in multiple ways (for example, you can insert a number $$$x$$$ to the left or right of the original number $$$x$$$ in array $$$a$$$). What's the number of different ways?
It's actually the "value", that is, the number of occurrances of $$$a$$$. Use the fact that "only one number can be inserted into each space" to prove.
Read the editorial for I1 and the hints first.
According to the hint, you can count the number of ways to insert the new numbers into the space, so the dp and transitions are similar to those in problem I1.
We can add an additional dp array, $$$g_{i, j}$$$ representing the number of different ways when everything meets the description of $$$f_{i, j}$$$. Let's see from which values it can be transferred:
- If $$$f_{i, j} = v_i$$$, then $$$f_{i, j}$$$ can only be transferred from $$$f_{i-1, j-a_i}$$$. That is, $$$g_{i, j} = g_{i-1, j-a_i}$$$.
- If $$$f_{i, j} = v_i + 1$$$, then $$$f_{i, j} = \sum_{k \in L_i, f_{i-1, k} = f_{i, j} - 1} g_{i-1, k}$$$.
We can use some tags and a Deque to maintain the whole process, so the amortized time complexity is $$$\mathcal O(n)$$$.
#include <bits/stdc++.h>
namespace FastIO {
template <typename T> inline T read() { T x = 0, w = 0; char ch = getchar(); while (ch < '0' || ch > '9') w |= (ch == '-'), ch = getchar(); while ('0' <= ch && ch <= '9') x = x * 10 + (ch ^ '0'), ch = getchar(); return w ? -x : x; }
template <typename T> inline void write(T x) { if (!x) return; write<T>(x / 10), putchar((x % 10) ^ '0'); }
template <typename T> inline void print(T x) { if (x > 0) write<T>(x); else if (x < 0) putchar('-'), write<T>(-x); else putchar('0'); }
template <typename T> inline void print(T x, char en) { print<T>(x), putchar(en); }
}; using namespace FastIO;
const int MOD = 998244353;
namespace Modint {
inline int add(int x, int y) { return (x += y) >= MOD ? x - MOD : x; }
inline int sub(int x, int y) { return x < y ? x - y + MOD : x - y; }
inline int mul(int x, int y) { return 1ll * x * y % MOD; }
inline int pow(int x, int y) { int r = 1; for (; y; y >>= 1, x = mul(x, x)) if (y & 1) r = mul(r, x); return r; }
inline int inv(int x) { return pow(x, MOD - 2); }
};
struct modint {
int v;
modint (int x = 0) : v(x) { /* for debug only. assert(0 <= x && x < MOD); */ }
inline int get() { return v; }
modint operator - () const { return v ? MOD - v : 0; }
modint operator + (const modint &k) const { return Modint::add(v, k.v); }
modint operator - (const modint &k) const { return Modint::sub(v, k.v); }
modint operator * (const modint &k) const { return Modint::mul(v, k.v); }
modint operator / (const modint &k) const { return Modint::mul(v, Modint::inv(k.v)); }
modint pow(const modint &k) const { return Modint::pow(v, k.v); }
modint inverse() const { return Modint::inv(v); }
modint operator += (const modint &k) { (v += k.v) >= MOD && (v -= MOD); return *this; }
modint operator -= (const modint &k) { (v -= k.v) < 0 && (v += MOD); return *this; }
modint operator *= (const modint &k) { return v = Modint::mul(v, k.v); }
modint operator /= (const modint &k) { return v = Modint::mul(v, Modint::inv(k.v)); }
};
struct Node {
int f; modint g; long long len;
Node () {}
Node (int F, int G, long long L) : f(F), g(G), len(L) {}
Node (int F, modint G, long long L) : f(F), g(G), len(L) {}
}; std::deque<Node> Q;
#define MAXN 3000001
int a[MAXN];
void solve() {
int N = read<int>(); long long p = 0, l = 0, r = 0, v = 0;
for (int i = 1; i <= N; ++i) p += (a[i] = read<int>());
for (int i = 1; i <= N; ++i) assert (std::abs(a[i]) <= p);
Q.clear(); Q.push_back(Node(0, 1, 1)), Q.push_back(Node(1, 1, p));
modint gv = 1, gz = p % MOD, tv = 0, tz = 0;
for (int i = 1; i <= N; ++i) if (a[i] >= 0) {
for (long long ls = a[i]; ls > 0; ) {
Node k = Q.back(); Q.pop_back();
if (ls < k.len) Q.push_back(Node(k.f, k.g, k.len - ls)), k.len = ls;
(k.f == v ? gv : gz) -= k.g * (k.len % MOD), ls -= k.len;
}
l += a[i], r = std::min(r + a[i], p);
if (l > r) ++v, l = a[i], r = p, gv = gz, tv = tz, gz = tz = 0;
gz += -tz * (a[i] >= MOD ? a[i] - MOD : a[i]);
if (a[i] > 0) Q.push_front(Node(v + 1, -tz, a[i]));
tz += gv + tv * ((r - l + 1) % MOD);
} else if (a[i] < 0) {
a[i] = -a[i];
for (long long ls = a[i]; ls > 0; ) {
Node k = Q.front(); Q.pop_front();
if (ls < k.len) Q.push_front(Node(k.f, k.g, k.len - ls)), k.len = ls;
(k.f == v ? gv : gz) -= k.g * (k.len % MOD), ls -= k.len;
}
r -= a[i], l = std::max(l - a[i], 0ll);
if (l > r) ++v, l = 0, r = p - a[i], gv = gz, tv = tz, gz = tz = 0;
gz += -tz * (a[i] >= MOD ? a[i] - MOD : a[i]), Q.push_back(Node(v + 1, -tz, a[i])), tz += gv + tv * ((r - l + 1) % MOD);
}
print<int>((Q.back().g + (r == p ? tv : tz)).get(), '\n');
}
int main() { int T = read<int>(); while (T--) solve(); return 0; }
Try to solve the initial problem: count the number of valid array $$$b$$$ for $$$n\le 500$$$.
Consider $$$f_{i,j,k}$$$: the number of ways to fill the first $$$i$$$ elements of $$$b$$$, which contains at most $$$j$$$ first elements from $$$a$$$ as a subsequence, and the sum of the first $$$i$$$ elements is $$$k$$$.
Try to optimize this from $$$O(n^2s^2)$$$ to $$$O(n^2s)$$$, and then $$$O(\rm{poly}(n))$$$, and then $$$O(n^3)$$$.










Fun fact:
PS: It's three minutes before the contest starts.
Hi, is this a public discord channel that we can join? Would love to know more ppl.
D was a cool one imo
C and D was difficult or I fckd up
D was easy, C was tough i guess. I still can't figure out how to do it.
Why can't we just implement the procedure in the statement as it is?
Study examples in the statements and notice the values that we add to the result
The procedure is a divide and conquer. Split the problem in two halfs. Can you see any relation between the first and second half?
Can you quickly calc the second half given certain info about the first half? what are this info?
Let's say we know that there are x values counted in the first half with sum = y. How to calc the sum of values in second half in O(1)?
For each counted value in the first half, there is a corresponding value in the second half at the same index.
So, if you counted value number 5 in range [l, m], then you also count value number 5 in [m+l, r], for example.
Can you add few more hints. I get the general idea but am struggling to derive the solution from it.
This solution uses recursion so you need to be comfortable with that.
You can check this explanation and the image https://codeforces.me/blog/entry/137621?#comment-1233115
Thanks. Got it.
you can think about the sum of AP at each level and add the sum to your final answer
Sucks could've solved E if I had known how to do tabulation DP. My memoization with unordered_map didn't pass even though O(n) complexity.
Are you sure your code is O(n)?
Consider a tree with 1 internal node and n leaves.
Yeah I guess that would iterate O(n^2) so I would need some other method.
Fast editorial forces
predicting [800, 3000] for I is diabolical
I really enjoyed in solving B!!(although am a noob:( )
I liked I1 very much, it was very fun
_istil I believe the model solution for I2 (as well as the solution I was trying to write, and all the ones that have AC) are wrong — they might overcount arrays $$$b$$$ with consecutive equal elements.
For example, on
the solution outputs 6 but I could only find the following 5 solutions with exhaustive search:
(I believe the last solution is being double counted.) Can this be addressed?
This is very disappointing: I believe the same, and currently, we are discussing the issue.
The most boring solution is to change the statement so that it fits the code, but that's too stupid.
As someone who did not solve either version of I2 during the contest, I would prefer that I2 just be removed from the contest. :)
(After all, none of the solutions that currently have AC are actually correct ...)
I think in this case (expected extremely hard problem turns out to be almost unsolved + wrong), this would be best:
As I understand it, accepted solutions are counting pairs (B, mask) where B[mask] = A instead of just counting sequences B? That should be easily editable and as long as there's no other mistake, it's kind of a waste to remove a prepared and published problem.
Also when prizes are involved, give out prizes based on the corrected standings after item 1. While trying to solve I2 could've given someone a worse spot than if the problem was correct, unfortunately it's impossible to prove so anyone who got a prize but lost rating can only choose between accepting both or rejecting both, and it has to be a choice by contestant.
I agree with most of your points (people who were adversely affected can petition to have the contest unrated, statement can be changed to reflect the official solution, fine to keep this problem for practice purposes).
But I don't think it makes sense to have this problem count towards the contest standings given that the ACs do not correctly solve the problem statement that was given in-contest.
Yeah, that's a valid point.
I doubt this point. This time >=150 people solved I1, so I suppose most of those people got non-trivial information about what I2 is, and I wouldn't say the number of people who put some effort on I2 is "almost nobody" — well this is a subjective word, but I would say more than half of people in the battle in rating >=3000 got unfair effect changing their ranks.
(Not an opinion from my personal point of view; I read I2 but spent only a few minutes, so my rating drop was just about right or should have even been larger.)
For being unrated or not, it's up to how Codeforces values on the rating. Perhaps rating is just a number.
The information "go for I1, it's pretty easy!" is in the standings — I definitely took advantage of it, even though I often check first subtask of hard problems, I otherwise avoid spending significant time on it or keep it for last. If you've used that information, you've most likely looked at the standings after and saw that the number of solutions for I2 is vastly lower, so it should be treated as a super hard final problem and not as something with similar difficulty.
Either way, anyone who hasn't submitted for I2 won't be directly affected by official solution being wrong; those who submitted and didn't fail sample are like 10 people, and they can request getting contest skipped.
The decision making process regarding how much time to spend before submitting isn't affected either since it's a hard subtask that mimics a hard subtask.
This is ultimately about choosing the least bad option (unrated is Exterminatus, when any attempts to salvage the situation are worse than making it all gone — admittedly a very common situation), about how to deal with effects of the wrong solution+tests. There's a ripple effect on those who don't submit, but compared to a general mistake to spend a lot of time on [hardest problem hardest subtask almost no solutions], it should be very small, so this is a salvageable situation.
For me, the solution of I1 gives (or hints) you a direct way to solve the wrong version of I2. I would expect at least half of the people who solved I1 were affected.
What does that have to do with the official solution being wrong? I don't understand. It's your choice to solve the wrong version.
In other words, if there was a correct official solution for I2, what would've changed for everyone who got "hinted" at wrong solution by I1? Note the actual number of people who submitted anything and passed pretest 1 is visible.
Unfortunately, pretest 1 was wrong.
Oh. That's a much bigger problem. I was working on the assumption of "as long as there's no other mistake". That's certainly pushing it into unrated territory, especially combined with O(N^2) passing on E.
I don't understand your point. People stop writing when they realize it is wrong.
Did you read this and this? Under that assumption (applies to everything that I wrote above), people would only realise it's wrong once they submit and pass pretest 1, and we know that number to be very small. None of what you wrote matters, they're complete non-sequiturs, what matters is that the assumption I made was wrong.
Well, for E, inefficient time complexity passing a problem is something that happens all the time, and it's not a real issue (problemsetters can't predict every wrong approach of the problem). The pattern needed to hack your solution was not one of the typical tree shapes, so probably they missed it. I didn't find too many other solutions that can be hacked with the same test either.
Why would people only realize it's wrong once they submit and pass pretest 1 even given your assumption? (What even is your assumption though?)
No matter what was happening in the pretest 1, why can't you like this comment, notice it is wrong during coding or before coding? This has nothing to do with any of your assumption about pretest 1.
My point is, the wrong version of I2 is not that hard given that you have solved I1. After solving I1, people spent time noticing the wrong version of I2 is not the correct problem statement, and concluded that I2 is nontrivial. They(We) are definitely affected by the wrong I2.
and what changes for they(you) from the scenario where I2 was solvable but hard?
there is no difference from your perspective....
You're asking me about things in the linked comments. Read. That's literally all you need to answer your own questions: reading&comprehension.
That's quite surprising considering it's a simple dumb code that I quickly put together because end of the contest was close. It's not even something I fully thought up by myself, just inspired by some stuff I've seen, though badly applied.
Oh well, unlucky some times, lucky other times.
Is there any precedent to this? The closest I can think of is this problem and the entire div.1 was unrated.
Last year at GoodBye2023 there were also some mistakes by the authors, which seemed to me to be much larger. So I hope that this next year will be better than the previous one)
I also wonder if anyone was able to come up with the right solution for I2 or is it impossible?
P.S. Also here is my experience of solving this problem: looked closely at the code for I1 -> hmm this should be improved to I2 by simply adding a few structures -> started writing the code -> after 5 minutes realized that some arrays are taken into account several times -> stop writing -> think -> go to problem H.
Overall a tough contest
Why did my code for E get TLE even though I think my code is O(nlogn)?
298891273
I also had O(n) code that got TLE. Can someone please explain why? Thanks!
Consider a tree with 1 internal node and n leaves.
Do you know where it specifically is getting TLE?
Then,
For p.first=1.Since you have n edges in the node,and for all edges you will visit all edges again,which leads to $$$O(n^2)$$$
Great round! Love it
Centroid decomposition for E 298885664 Can this be hacked?
In A what if the test case array is 115,9,110. Should it be yes because in question it said partition can range from 1 to n.
The answer is NO in this case as there's only ONE way for partitioning: [115], [9], [110]
The partitioning size in question was written. 1 to n so can't it be the complete array of all elements ie [115,9,110]
if you choose the complete array, the triplet $$$(9, 9, 110)$$$ can't form a triangle. Note how the elements of the triplets do not need to be distinct.
what was the intuition behind c today, can anybody help? i spent almost 2 hours thinking of how to approach it
Well if you plot the answers for some smaller value , you can see that it follows a set pattern . So for every subtree for which you know the answer you can find the value for its adjacent tree.
I used a bottom up approach and started from the smallest valid group up to the actual value of n and handled the odd and even cases differently.
My submission : 298887432
Let's think about maintaining the following variables at each level:
Then it's possible to calculate the sum of lucky values for the current level (if $$$w$$$ is odd).
Let's write the values of $$$c$$$, $$$w$$$ and $$$s$$$ at level $$$i$$$ as $$$c_i$$$, $$$w_i$$$ and $$$s_i$$$.
Initially, $$$c_1=1$$$, $$$w_1=n$$$, and $$$s_1=1$$$. At level $$$i$$$, do the following:
Let's say the $$$j$$$-th segment is $$$[a_j, \ldots, a_j+w_i-1]$$$ ($$$1 \le j \le c_i$$$). If $$$w_i$$$ is even, the segment is split as $$$[a_j, \ldots, a_j+w_{i+1}-1], [a_j+w_{i+1}, \ldots, a_j+w_i-1]$$$. Then, $$$s_{i+1}$$$ is calculated like:
The odd case and the sum of lucky values can be handled in the same way.
Thanks! After 30 minutes of thinking I figured out why your fomulas actually work. Nice and neat solution.
Nevertheless, don't know how to come up with this during round. It's more of intuition, I know, and should be trained by constant practicing, but anyway a bit sad that constructive problems cannot be trained constructively :(
It was not easy for me, either. I was stuck in this problem for a long time (I actually solved D much faster). After many failed attempts, I suddenly realized $$$s$$$ is a good summary of the current split of segments.
Maybe the key insight here is that the shape of all segments is similar. Let's say we have segments $$$[1, 2, 3, 4, 5]$$$ and $$$[6, 7, 8, 9, 10]$$$. In the next level we'll have four segments split like $$$[[1, 2], *, [4, 5]]$$$, $$$[[6, 7], *, [9, 10]]$$$ (where $$$ * $$$ denotes the removed elements). We can generalize each segment as $$$[[a, a+1], *, [a+3, a+4]]$$$ -- that is, relative offsets within each segment are the same among all segments. Then you might be able to derive that $$$s$$$ can be used to represent the current segment split.
thank you very much!
Wow, this is a very neat explanation, and appropriate for lower rateds like me who are having problems solving C. Thank you! I couldn't make progress at all with the official editorial but with this explanation, I could derive the same formulas and implement a correct solution in less than 20 minutes. Wish I thought of this during the contest :) Thank you very much!
@_TernaryTree_
Could you help me review my code which is very much similar to yours? I did somewhat like this,
for reference , my sub: 298897695
while this worked for first 5 pretest cases , it failed on 6th one but i find it interesting how this pattern works. now,
why does your approach works but mine fails? why did you initialise mul as (n+1) and not the first value which we get if the segment length is odd? i mean how did this idea hit? except for the last case which i could not simulate , my idea for mul(==c) works good till pretc 5.
why do you apply /2 after multiplying sum and mul? why not do mul / 2 before ?
nevertheless, Appreciated the round. Thank you.
Can it be tried using the recursion? If we can reduce the TC somehow?
not without involving dp or maths.
tried using dp to store the results but not working
check my submission, i think the problem is how you calculate c
Yes. It is how i calculate c which is the issue here.
Also. I figured out why this solution works. Great question. Great solution.
can you post your updated code and explain line by line why it works i just kinda coded until it passed, idk
What are x and y in C? Could somebody please explain?
The parent segment gets divided in 2 subsegments, x and y are middle index of that subsegment. And x + y = n + 1.
Ex: n = 22 , k = 4 First Segment : [1 , 2 .. . . 22] as Even length so subsegment [l , m] & [m+1 , r].
Second Segment : [1 , 2 , ..... 11] & [12 , 13 , .... 22]
Here x = 6 , y = 17 and x + y = 23 which is 22 + 1.
I have not discussed about [12 , 13 ... 22] you can analyse it.
Third Segment : [1 , 2 .. 5] & [6] & [7 , 8 , ,... 11] as Odd length so subsegment [l , m-1] & [m] & [m+1 , r].
Here x = 3 , y = 9 and x + y = 12 which 11 + 1.
For A, why 10, 2, 10 is not a valid answer? 10 + 2 > 10 10 + 10 > 2 2 + 10 > 10
the set{10,2} has 2 possible triplets
10 10 2
and
2 2 10
only one of these is valid
its a valid answer , but the question says for all possible combinations.
i.e , if you are choosing a segment [2,10] then all the combinatoins 2,2,10 and 10,10,2 must satisfy this condition , but 2 + 2 is not greater than 10 that's why it will not be the case.
Didn't notice "for all possible combinations" part :'[ Tnx
i don't understand editorial for C, who can help me?
check my solution, I produced it after slogging 3 hours on it.
such a brick problem
I check your solution later , I am so tired , but thank you for reply
getting TLE on B, seems like approach is fine , but I am missing some basic stuff.
Can anyone check my solution? https://codeforces.me/contest/2053/submission/298900263
P.S. got the issue, it was related to size of vector.
In your code,
Each testcase independently allocates 8e5 ints. However if you have
t=10000testcases, your program will end up allocates roughly 8e9 ints, which causes a TLE.simply changing your
szto2*n+1will get an ACYeah,got it vro.
Thank You
_istil I believe there is a typo in the DP transition for problem F, the correct transition should be
Why $$$max(f_{i - 1, w})$$$ and not $$$max(f_{i - 1, w} + c_{i - 1}d_{i, w})$$$? Why $$$d_{i, w} = 0$$$? We only have $$$d_{i, j} = d_{i - 1, j} = 0$$$ and no constraints on $$$w$$$.
For
H, I'm not seeing how the answer isn*(w-1)forw>=3.If
n=3,w=5,a=[3,3,3]Shouldn't answer be
sum([3,4,5])=12and not14??Am I missing something??
you can first make the array equal to [3,3,5] in one move and then make it equal to [4,5,5] in the next, making the sum equal to 14. Notice that the condition is that a_i is different only to a_(i+1) and it doesn't specify that for example it has to be different from a_(i-1).
Question D:
what's the logic behind qpow in code present in tutorial? I know that we have to remove the previous xth value and then update with new xth value if needed
I didn't understand this at first either, but it's a consequence of Fermat's little theorem. If X is prime, then for any integer A:
A ^ (X - 1) = 1 mod XThen we can multiply both parts by our previous answer Y:
Y * A ^ (X - 1) = Y mod X(if Y < X, which is true, because we took modulo of Y earlier)So if Y is our previous answer, and we need to divide it by A modulo X, we get:
(Y * A ^ (X - 1)) / A = Y * A ^ (X - 2)qpowitself is a function, which calculatesmod - 2power of number modulomod.Thanks for explaining
When you are dividing A by B and taking mod with m, you need to instead multiply A by modular multiplicative inverse (modinverse) of B with respect to m.
If m is prime, modinverse is calculated as pow(B, m-2)
Hence, in this case, (A/B)%m == (A * pow(B, m-2))
thanks for explaining
great round! better than goodbye 2023 :) ehehe
can anyone please explain the last test case for problem C? 8765432 is apperantly a randomly choiced even number no where close to power of 2 and yet it get all the score from 1 to itself.
however that's not true for input like
6 1which has only score of 3When $$$k=1$$$, Iris observes all of the stars for any $$$n$$$.
oh, that makes sense. thank you for the explaination
//
I love the coordinator's (or anybody else who answers the questions) work for the problem E. Nothing in the statement says that we will change $$$p$$$ or $$$q$$$, only some sequence of vertices. So I asked the question about it, and their answer was brilliant...
It's written "whenever p is a leaf, Nora wins, whenever q is a leaf, Aron wins. If INITIALLY p and q are both leaves, it's a tie". If p and q weren't changing then this statement wouldn't make sense.
But there is no word in the statement that says that $$$p, q$$$ are changing, so I asked to confirm my guess. Why didn't they answer with a word "yes", instead they referred to the statement ?
Maybe they just misunderstood your question. For example, I read it as "can the first player only move the head and the second — only the tail?" at first
While I agree that the fact that $$$p$$$ and $$$q$$$ are moving is rather obvious, it isn't explicitly written anywhere, so the answer to the question should contain that information.
Can D be solved Without Using the Binary_search in between the implementation We can store the {l,r} for each and every unique element as the starting and the ending index and whenever we want to change particular index we take the value of that and take the first element of it from the range {elel,eler} where elel=left indx of element and eler=right index(starting or ending index in the sorted array) and give the element rth(right) index to the element+1, and the lth(left) index and rest from (l-1,l,l+1,...,r-1) all are ele so there would be no change and perform the operations accordingly.
Sorry for bad English.
Sorry, I don't understand the editorial for C. Since higher rated people likely don't need tutorial to solve C, can you explain it in a way that is understandable to us lower rated folks?
The solution comes down to a single observation that if
[l,m1]and[m2,r]are two halves of the segment[l,r], then the values we add to the answer while processing[m2,r]are the same as the values we add while processing[l,m1]just shifted by(l+r)/2.Thank you but how does that help us when there are 4 segments, 8 segments, etc?
You never have to consider these cases explicitly. The point is that we don't need to process
[m2,r], so we split only[l,m1]and apply our observation recursively.Can anyone help me with understanding the solution to the problem C? The editorial is not quite helpful to me, not sure what x & y they have assumed.
so imagine n=22, k=4
since we have an even length, we need to split the array into [1,11] and [12,22]. now both subarrays are odd length, so we need to add their middle index, which is 6 and 17. in this case, x=6 and y=17, where x+y = 6+17 = 23 (notice how it's n+1)
moving on to the next split, we have 3+9+14+20 = 46 (notice how it's 2*(n+1)). so we can generalize that each split downwards multiplies (n+1) by 2, and we should add this value if the current subarray length is odd.
if n is odd, we can add ceil((n+1)/2) to the answer
Thanks so much for explanation!
Wowwww!! This is super explanation!! Really Helpful. Thank you and keep it up!
Can anyone please explain this testcase in problem B:
5
1 1
3 3
4 4
2 3
1 2
I think we cannot have a unique impression simultaneously for i = 4 and i = 5, please help with this.
It means when you consider for $$$i=4$$$,you don't need to consider $$$i=5$$$,and so on.
somehow the approach for B was not as intuitive to me during practice, I ended up implementing a solution on the same lines as that of prefix sum but in a different way, could someone help me by looking at the submission to let me know if I complicated it a bit and there does exist an easier workaround at some point . Submission
in the editorial solution of C ,in the line at the end: cout << mul * sum / 2 << endl; why it has been multiplied by mul?can anyone explain..
because we have modified the n in while loop
Can we please normalise mentioning what [.] operation stands for (whether it is ceil or floor)? (C did not specify what it exactly was)
Floor: ⌊x⌋
Ceil: ⌈x⌉
okay thanks :)
Whenever not explicitly mentioned, we must assume floor.
Can somebody help me with my code for problem B. 298926051 298926337
The only difference between the two codes is a commented code at the end of second submission. But the outputs for the first test case are different. How is that possible?
Even if you simply put this at the end of the code it says segmentation fault. It's because you are using n in your code and then kind of redeclaring it even though its commented out. To check this simple change the variable n in the above commented code to some other variable which you did not use in the code (some thing like "var") then it works.
TLDR : using the variable name again (even though commented out)
Could someone help me understand why my code for E 298930084 is giving TLE? I am probably doing something stupid somewhere but can't spot it.
Edit: Never mind, I found the mistake.
Can somebody tell me, why this code produces wrong answer on the last case of sample.
I am only calculating left segment answer, and the answer right segment is calculated by adding how many nodes contributed in left segment * m , the i add both of them.
Can D be solved Without Using the Binary_search in between the implementation We can store the {l,r} for each and every unique element as the starting and the ending index and whenever we want to change particular index we take the value of that and take the first element of it from the range {elel,eler} where elel=left indx of element and eler=right index(starting or ending index in the sorted array) and give the element rth(right) index to the element+1, and the lth(left) index and rest from (l-1,l,l+1,...,r-1) all are ele so there would be no change and perform the operations accordingly.
Sorry for bad English. Please can someone tell.
Yes. I wrote an O(T(n+logp)) 299126498 before contest(if consider radixsort to be O(n)).
Thanks.
Can anyone explain the solution for C which is given in the editorial.
BTW the quality of the editorial can be improved a lot!!!
Can anyone explain question C (what's going on)
https://codeforces.me/blog/entry/137621?#comment-1233115
Thanks for the Editorial!
For problem F, I think there is a missing term, namely: c[i-1]*d[i][w], on the left side of fij relation. Is this true or I'm missing something?
Yup I think you are right, it's also present in correct submissions 298871838
for problem C, I had the following code. ~~~~~ This is my code. t = int(input()) for i in range(t): n, k = map(int, input().split()) binary_n = bin(n)[2:] binary_k = bin(k)[2:] digit_count_n = len(binary_n) digit_count_k = len(binary_k) diff = digit_count_n — digit_count_k #this is non negative considerate_n = int(binary_n[:digit_count_k]) if considerate_n >= int(binary_k): iterations = diff + 1 else: iterations = diff new_diff = digit_count_n — iterations multiplier = int(binary_n[new_diff:], 2) increaser = (n + 1) / 2 print(int(multiplier * increaser)) ~~~~~
I checked using python's hypothesis library, if the code given in the solution, and my code return different answer in any case, it couldn't find any example. I am now very very sure my solution is correct, though I may be wrong. But it says failed on pretest 6. Can anyone please help, what should i do?
for Problem C can anyone help me out in this submission 298817735 how he come up with the calculation for top_left? its(ecnerwala's soln btw)
The code does pretty much the same thing as explained in my comment. Take a look at it.
thankss
Can someone explain the solution of Problem B?
If we want to find the answer for some interval i, we need to try every value v between li and ri and check whether we can choose a value that is different form v for every other interval. Well, for every interval with length at least 2, we can always choose a value form this interval that is not equal to v. So our problem is only in intervals i such that li equals ri, because for those we must choose li as their values. So the problem is going to be like this: For each interval i with length at least 2, find out whether there is a value li <= v <= ri such that there is no other interval j: lj = rj = v. To do this, we can build an array f that is initially filled with zeros, and for every 1-lengthed interval i we assign f[li] = 1. Now to find the answer for interval i, we just need to check if there is some value li <= v <= ri such that f[v] = 0 i.e. the values from f[li..ri] are not all ones. Here, it's enough to calculate the sum of values f[li..ri] and compare it with the length of the interval ri-li+1. To calculate the sums efficiently you can use prefix sum. Note that intervals with length 1 need to be handled separately, just check if the interval [li, ri] occurs no more than once.
Here is my implementation: 298817661
why This code giving me TLE for Problem D, am I missing Out something?, I think time complexity for the code will be O(qlogn + nlogn).
OrderedMultiset is way too slow. I also struggle with using it in contest, but after I realized that I can use just vector.
Problem B is not a good problem from anypoint , it is done only by observing of given testcases not by any good logic.
It is a good problem, all you had to is fundamentally think if you have to somehow make i unique, what all thingies can trouble you. At the end you'll realize that any number that has atleast 2 values can never cause i to lose uniqueness, only the ones with l==r can,from then on its on your implementation skills how you will efficiently handle this.
Overall a hard contest. Couldn't solve C. B and D are good but very doable questions. I did a bad lengthy imple for D but otherwise it's fine.
Will try to explain Part 4. of $$$E$$$.
For Aron to win on $$$k = 2$$$, he must
$$$-$$$ reach a node $$$q$$$ that is adjacent to at-least 1 leaf.
$$$-$$$ from a node $$$q'$$$ which is not a leaf.
For a node $$$q$$$ to be adjacent to at-least $$$1$$$ leaf-
$$$1.$$$ $$$degree[q] > 1$$$
$$$2.$$$ $$$d[q] ≠ degree[q]$$$ where $$$d[q] =$$$
number of adjacent nodes to q that are not leaves.Number of potential $$$q'$$$ for $$$q$$$ is equal to $$$d[q]$$$. One of them will be on the simple path $$$(p, q)$$$. So we do $$$d[q] - 1$$$ as explained in the editorial.
Is there a way to check my submission to I2 on the contest day? I don’t mind if it’s removed from the contest results, but I would like to confirm the submission itself.
In problem F, "The transfer should be as follows:
fi,j=max(max1≤w≤k(fi−1,w+ci⋅di−1,j),fi−1,j+(di,j+ci)⋅(di−1,j+ci−1)−di,jdi−1,j)."
If the matrix is
+1 +1 -1
+1 -1 -1 (let k=2)
f[1] = (0,0,0)
f[2][2] = f[1][w]+c[2]*d[1][2] = 0+2*0 = 0 OR 0+2*1-0=2
f[2][2] = 2
But in the matrix
1 1 1
1 2 2
f[2][2] = 3
Shouldnt the transition be max(fi-1,w + ci.di-1,j + ci-1.di,w? How are we taking into account the '' ci-1.di,w '' term?
Is there a typo in solution for problem G?
I believe you are talking about common shortest period between $$$X$$$ and $$$Y$$$? Or am I missing something?
In the editorial for E it is said:
Can someone explain what the function f does, and what f(p,q) is? I think I misread something.
There's something wrong with both linear and log codes of problem G.
Hack:
answer should be 001000, but all the solutions and even solutions on Luogu output 000000.
Let's mention our dear child irr74.
Edit: It seems that
irris.cpp,irris-32bit.cpp,LMydd0225_hash.cpp(3 solutions on Polygon marked as correct) are all wrong.Edit 2: After checking all in-contest submissions, there are three solutions hacked:
You can say whatever you want, but I don't think it's fun when I'm busy working on the problem while you are busy sending comments in every chat group to try to satirize me on this and that.
There is a typo in the first picture of G's solution: the string is $$$\tt{abaabaabaabaaba\color{green}{ba}}$$$, instead of $$$\tt{abaabaabaabaaba\color{red}{ab}}$$$.
This is not a typo. I intentionally used this example, even though it looks very similar to hacking data.
But in the picture here the last two characters of the string is
ba.(And it says that the rightmost position is invalid, so I think the picture here is wrong.)
Sorry, I misunderstood your meaning. I did write it wrong. I have corrected it. Thank you.
In Tender Carpenter problem, if the input is 5 2 4 then the editorial solution gives "NO" but the answer should be "YES", we can still partition it in two ways:-
[5],[2],[4] and [5,2,4]
5 + 2 > 4
5 + 4 > 2
2 + 4 > 5
Can someone please correct me on this if I am wrong?
If you choose a set of elements, you will need to test if evry possible formed triangle is valid or not.
For example, for a set of size 1 like [5], only one triangle is possible which is {5,5,5}.
for a set of size 2 like [2,3], many triangles are possible which are {2,2,2},{2,2,3},{2,3,3}...
for a set of size 3 like [5,2,4], a lot of triangles are possible all of which need to be valid but some of them are not like {2,2,4},{2,5,2} etc.
You may ask if you still have any doubt.
Ah, I understand. Thank you for the clear explanation :)
No Problem, happy coding
There seems to be an issue with both the linear and logarithmic solutions for Problem G. For instance, the test case 1 8 8 abaabaab abaababa should yield the output 001000, but all the current solutions, including those on Luogu, produce 000000 instead.
Is E's editorial poorly written or did I miss something? What is function f? They never defined it
The editorial for E is not written in a very comprehensible way. Reading the provided source code is better, imo. From my understanding, $$$f(p,q)$$$ denotes the "second tail" of the caterpillar. It can be seen as the node (that's on the caterpillar's body) directly adjacent to the caterpillar's tail.
thank you. i was stuck here.