A. Again Twenty Five!
The problem of getting the last two digits is equivalent to the problem of getting the number modulo 100. So we need to calculate  . According to the rules of modular arithmetic
. According to the rules of modular arithmetic
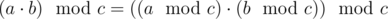
So
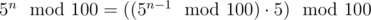
Let's note that 52 = 25. Then
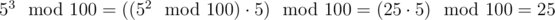
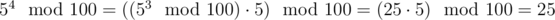
And so on. All  are equal to 25 for all n ≥ 2.
are equal to 25 for all n ≥ 2.
So to solve the problem one need to just output 25. There is no need to read n.
B. Moore's Law
Every second the number is multiplied by 1.000000011. Multiplication several times to the same number is equivalent to exponentiation. So the formula is n·1.000000011t (1.000000011 raised to the power of t and then multiplied to n). In a program one should not use a loop to calculate power as it is too slow for such big n, usually a programming language provides a function for exponentiation such as pow.
C. Lucky Numbers
There are 2 lucky numbers of the length 1. They are 7 and 8. There are 4 lucky numbers of the length 2. They are 77, 78, 87 and 88. There are 8 lucky numbers of the length 3. They are 777, 778, 787, 788, 877, 878, 887, 888. For each addition of 1 to the length the number of lucky numbers is increased times 2. It is easy to prove: to any number of the previous length one can append 7 or 8, so one number of the prevous length creates two numbers of the next length.
So for the length n the amount of lucky numbers of the length \textit{exactly} n is 2n. But in the problem we need the amount of lucky numbers of length \textit{not greater} than n. Let's sum up them. 21 = 2, 21 + 22 = 2 + 4 = 6, 21 + 22 + 23 = 2 + 4 + 8 = 14, 21 + 22 + 23 + 24 = 2 + 4 + 8 + 16 = 30. One can notice that the sum of all previous powers of two is equal to the next power of two minus the first power of two. So the answer to the problem is 2n + 1 - 2.
One of the possible implementations of 2n + 1 in a programming language is to shift 1 bitwise to the left for n + 1 binary digits or to shift 2 bitwise to the left for n binary digits. For example, in Java the problem answer formula is (2L << n) - 2, in C++ is (2LL << n) - 2. Suffixes L and LL correspondingly are required so that result of the shift expression have 64-bit integer type (long in Java and long long in C++). Type of the second operand does not matter for the type of shift expression, only the type of the first operand. Also parenthesis are required because without them subtraction is performed first and only then bitwise shift.
D. Hexagons!
Let's count the number of cells having the distance of exactly n. For n = 0 it is 1, for n = 1 it is 6, for n = 2 it is 12, for n = 3 it is 18 and so on. One can notice that n = 0 is a special case, and then the amount increases by addition of 6. These numbers form an arithmetic progression. In the problem we need to sum these numbers. The formula of the sum of an arithmetic progression is (first + last)·amount / 2. The first is 6, the last is 6n, the amount is n. So the sum is (6 + 6n)n / 2 = 3(n + 1)n. And plus 1 that is not in the arithmetic progression. So the final formula is 1 + 3n(n + 1).
To avoid overflow, multiplication in the formula should be performed in 64-bit integer type. For this either 3 or 1 or n should have 64-bit integer type. The literals are 64-bit integer when they have suffix L in Java or LL in C++.
E. A rectangle
Let's see how the number of affected cells changes depending on the column. For example 3, 2, 3, 2, 3. That is it alternates between the size of the first column and the size of the first column minus one. The amount of "minus ones" is the amount of columns divided by 2 rounded down. Without "minus ones" all columns have equal size and the total amount of cells is equal to size of the first column multiplied by the number of the columns. The first column size is (y2 - y1) / 2 + 1. The columns amount is x2 - x1 + 1. So the final formula is ((y2 - y1) / 2 + 1)·(x2 - x1 + 1) - (x2 - x1) / 2.
To avoid overflow, multiplication should be computed in 64-bit integer type.
F. Selection of Personnel
The amount of ways to choose a group of 5 people from n candidates is equal to the number of combinations 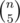 , the amount of ways to choose a group of 6 people from n candidates is
, the amount of ways to choose a group of 6 people from n candidates is 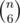 , the amount of ways to choose a group of 7 people from n candidates is
, the amount of ways to choose a group of 7 people from n candidates is 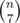 , the amount of ways to choose a group of 5, 6 or 7 people from n candidates is
, the amount of ways to choose a group of 5, 6 or 7 people from n candidates is 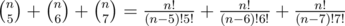 .
.
To avoid 64-bit integer overflow 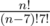 can be calculated in the following way:
can be calculated in the following way: n/1*(n-1)/2*(n-2)/3*(n-3)/4*(n-4)/5*(n-5)/6*(n-6)/7. Each division returns an integer because each prefix of this formula after division is also the number of combinations 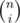 .
.
G. Challenge Pennants
First of all, ways to place both types of the pennants are independent. So each way to place "I fixed a critical bug" pennants on n tables is compatible to each way to place "I suggested a new feature" pennants on n tables. Therefore the answer of the problem is equal to the number of ways to place "I fixed a critical bug" pennants multiplied by the number of ways to place "I suggested a new feature" pennant.
The number of ways to place k identical items into n different places when any place can contain any amount of items is the definition of the number of k-combinations with repetitions or k-multicombinations. The formula for the number is 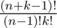 .
.
So the whole formula for the problem is 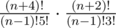 .
.
To avoid overflow of 64-bit integer type recommended formulas for computation are (n + 2) / 1 * (n + 1) / 2 * n / 3 and (n + 4) / 1 * (n + 3) / 2 * (n + 2) / 3 * (n + 1) / 4 * n / 5.
H. Benches
The number of ways to choose 5 east to west paths that will have benches from n is 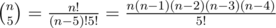 . There are n ways to place a bench on the first of these paths. Given the place of the first bench there are n - 1 ways to place a bench on the second of these paths because one of north to south paths is already taken. Given the places of the first and second benches there are n - 2 ways to place a bench on the third of these paths because two of north to south paths are already taken. And the same way n - 3 and n - 4 for the fourth and the fifth benches. Total number of ways to place benches on selected 5 east to west path is n(n - 1)(n - 2)(n - 3)(n - 4). So the formula for the problem is
. There are n ways to place a bench on the first of these paths. Given the place of the first bench there are n - 1 ways to place a bench on the second of these paths because one of north to south paths is already taken. Given the places of the first and second benches there are n - 2 ways to place a bench on the third of these paths because two of north to south paths are already taken. And the same way n - 3 and n - 4 for the fourth and the fifth benches. Total number of ways to place benches on selected 5 east to west path is n(n - 1)(n - 2)(n - 3)(n - 4). So the formula for the problem is 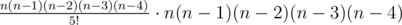 .
.
To avoid 64-bit integer overflow recommended order of computation is exactly as in the formula above, division should not be the last operation.
I. Parking Lot
There are the following ways to place n cars of the same make. They can be the first n, the last n, or they can be somewhere in the middle of the parking lot.
When n cars of the same make are the first or the last, there are 4 ways to choose the make of these n cars, then there are 3 ways to choose the make of one car adjacent to them (the make should be different from the make of n cars) and there are 4 ways to choose the make of each of the remaining n - 3 cars. So the formula for the case of n cars of the same make on either end of the parking lot is 4·3·4n - 3.
When n cars of the same make are situated somewhere in the middle, there are 4 ways to choose the make of these n cars, then there are 3 ways to choose the make of each of two cars adjacent to them (the makes of these two cars should be different from the make of n cars) and there are 4 ways to choose the make of each of the remaining n - 4 cars. So the formula for the case of n cars of the same make on a given position somewhere in the middle of the parking lot is 4·32·4n - 4.
There are 2 positions of n cars of the same make in the end of the parking lot and there are n - 4 positions of n cars of the same make somewhere in the middle of the parking lot. So the final formula is 2·4·3·4n - 3 + (n - 4)·4·32·4n - 4.
J. Divisibility
Let's factorize numbers from 2 to 10. 2 = 2, 3 = 3, 4 = 22, 5 = 5, 6 = 2·3, 7 = 7, 8 = 23, 9 = 32, 10 = 2·5. If a number is divisible by all numbers from 2 to 10, its factorization should contain 2 at least in the power of 3, 3 at least in the power of 2, 5 and 7 at least in the power of 1. So it can be written as x·23·32·5·7 = x·2520. So any number divisible by 2520 is divisible by all numbers from 2 to 10.
There are 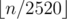 numbers from 1 to n divisible by all numbers from 2 to 10. In a programming language it is usually implemented as simple integer division.
numbers from 1 to n divisible by all numbers from 2 to 10. In a programming language it is usually implemented as simple integer division.







