A. Опять двадцать пять!

Задача нахождения последних двух цифр числа эквивалентна задаче нахождения числа по модулю 100. Таким образом, нам нужно вычислить . По правилам модульной арифметики

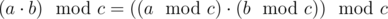
Таким образом,

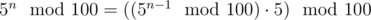
Заметим, что 5² = 25. Затем

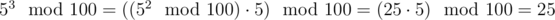
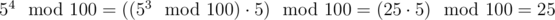
И так далее. Все равны 25 для всех n ≥ 2.

Таким образом, чтобы решить задачу, требуется всего лишь вывести число 25. Даже не требуется читать n.

B. Закон Мура

Каждую секунду число умножается на 1.000000011. Умножение несколько раз на одно и то же число эквивалентно возведению в степень. Таким образом, формула n·1.000000011^t (1.000000011 в степени t, умноженное на n). При написании программы не следует использовать цикл для вычисления степени, поскольку это слишком долго для такого большого n, обычно язык программирования предоставляет функцию для возведения в степень такую как pow.

C. Счастливые номера

Существует 2 счастливых номера длины 1. Это 7 и 8. Существует 4 счастливых номера длины 2. Это 77, 78, 87 и 88. Существует 8 счастливых номеров длины 3. Это 777, 778, 787, 788, 877, 878, 887, 888. При каждом добавлении 1 к длине числа количество счастливых номеров увеличивается в 2 раза. Это легко доказывается: к любому числу предыдущей длины можно дописать 7 или 8, так что число предыдущей длины создаёт два числа следующей длины.

Таким образом, для длины n количество счастливых номеров длины ровно n равно 2ⁿ. Но в задаче требуется найти количество счастливых номеров длины не более n. Давайте просуммируем их. 2¹ = 2, 2¹ + 2² = 2 + 4 = 6, 2¹ + 2² + 2³ = 2 + 4 + 8 = 14, 2¹ + 2² + 2³ + 2⁴ = 2 + 4 + 8 + 16 = 30. Можно заметить, что сумма всех предыдущих степеней двойки равна следующей степени двойки минус первая степень двойки. Так что ответ задачи 2^n + 1 - 2.

Одна из возможных реализаций формулы 2^n + 1 в языке программирования — это сдвинуть 1 побитово влево на n + 1 двоичный разряд или сдвинуть 2 побитово влево на n двоичных разрядов. Например, в Java формула ответа задачи (2L << n) - 2, в C++ (2LL << n) - 2. Суффиксы L и LL соответственно требуются, чтобы результат выражения сдвига имел 64-битный целый тип (long в Java и long long в C++). Тип второго операнда не влияет на тип выражения сдвига, только тип первого операнда. Также требуются скобки, поскольку без них сначала производится вычитание и только затем битовый сдвиг.

D. Шестиугольники!

Посчитаем количество ячеек, имеющих расстояние ровно n. Для n = 0 это 1, для n = 1 это 6, для n = 2 это 12, для n = 3 это 18 и так далее. Можно заметить, что n = 0 является особым случаем, а дальше количество увеличивается каждый раз на 6. Эти числа составляют арифметическую прогрессию. В задаче нам нужно просуммировать эти числа. Формула суммы арифметической прогрессии (первый + последний)·количество / 2. Первый 6, последний 6n, количество n. Сумма получается (6 + 6n)n / 2 = 3(n + 1)n. И плюс 1, которая не входит в арифметическую прогрессию. Таким образом, окончательная формула 1 + 3n(n + 1).

Чтобы избежать переполнения, умножение в формуле нужно выполнять в 64-битном целом типе. Для этого хотя бы один из членов выражения (3 или 1 или n) должен иметь 64-битный целый тип. Литералы имеют 64-битный целый тип, когда у них есть суффикс L в Java или LL в C++.

E. Прямоугольник

Посмотрим, как меняется количество затронутых ячеек в зависимости от столбца. Например, 3, 2, 3, 2, 3. То есть оно чередуется между размером первого столбца и размером первого столбца минус один. Количество "минус единиц" равно количеству столбцов делённому нацело на 2. Без "минус единиц" все столбцы имеют равный размер, и общее количество ячеек равно размеру первого столбца умноженному на количество столбцов. Размер первого столбца (y₂ - y₁) / 2 + 1. Количество столбцов x₂ - x₁ + 1. Таким образом, окончательная формула ((y₂ - y₁) / 2 + 1)·(x₂ - x₁ + 1) - (x₂ - x₁) / 2.

Чтобы избежать переполнения, произведение должно вычисляться в 64-битном целом типе.

F. Подбор кадров

Количество способов выбрать группу из 5 человек из n кандидатов равно количеству сочетаний C_n⁵, количество способов выбрать группу из 6 человек из n кандидатов равно C_n⁶, количество способов выбрать группу из 7 человек из n кандидатов равно C_n⁷, количество способов выбрать группу из 5, 6 или 7 человек из n кандидатов равно .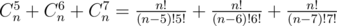

Чтобы избежать переполнения 64-битного целого типа, 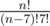можно вычислить следующим образом: n / 1 * (n - 1) / 2 * (n - 2) / 3 * (n - 3) / 4 * (n - 4) / 5 * (n - 5) / 6 * (n - 6) / 7. Каждое деление даёт целое число, поскольку каждый префикс этой формулы после деления также является числом сочетаний C_nⁱ.

G. Переходящие вымпелы

Прежде всего, способы разместить оба типа вымпелов независимы. То есть каждый способ разместить вымпелы "Исправил критичный баг" по n столам совместим с каждым способом разместить вымпелы "Предложил новую фичу" по n столам. Таким образом, ответ задачи равен количеству способов разместить вымпелы "Исправил критичный баг" умножить на количество способов разместить вымпелы "Предложил новую фичу".

Количество способов размещения k одинаковых вещей по n разным местам, когда каждое место может содержать любое количество вещей, является определением количества сочетаний с повторениями. Формула для нахождения этого количества .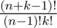

Таким образом, полная формула для задачи .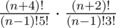

Чтобы избежать переполнения 64-битного целого типа рекомендуемые формулы для вычислений (n + 2) / 1 * (n + 1) / 2 * n / 3 и (n + 4) / 1 * (n + 3) / 2 * (n + 2) / 3 * (n + 1) / 4 * n / 5.

H. Скамейки

Количество способов выбрать 5 дорожек, идущих с востока на запад, на которых будут скамейки, из n составляет 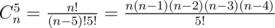. Есть n способов разместить скамейку на первой из этих дорожек. При фиксированном месте первой скамейки существует n - 1 способ размещения скамейки на второй из этих дорожек, потому что одна из дорожек, идущих с севера на юг, уже занята ранее расставленной скамейкой. При фиксированном месте первой и второй скамейки существует n - 2 способа размещения скамейки на третьей из этих дорожек, потому что две дорожки, идущие с севера на юг, уже заняты ранее расставленными скамейками. Аналогично получаем n - 3 и n - 4 для четвёртой и пятой скамеек. Общее количество способов разместить скамейки на выбранных 5 дорожках, идущих с востока на запад, составляет n(n - 1)(n - 2)(n - 3)(n - 4). Таким образом, формула для задачи .

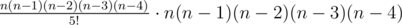Чтобы избежать переполнения 64-битного целого типа рекомендуемый порядок вычислений ровно такой как в формуле выше, деление не должно быть последней операцией.

I. Автостоянка

Есть следующие способы разместить n машин одной марки. Они могут быть первыми n, последними n, а также они могут быть где-то в середине стоянки.

Когда n машин одной марки первые или последние, существует 4 способа выбрать марку этих n машин, затем существует 3 способа выбрать марку одной машины, смежной с ними (марка должна отличаться от марки этих n машин), и 4 способа выбрать марку каждой из оставшихся n - 3 машин. Таким образом, формула для случая n машин одной марки на любом из концов стоянки 4·3·4^n - 3.

Когда n машин одной марки расположены где-то в середине стоянки, существует 4 способа выбрать марку этих n машин, затем существует 3 способа выбрать марку каждой из двух машин, соседствующих с ними (марки этих двух машин должны отличаться от марки этих n машин), и 4 способа выбрать марку каждой из оставшихся n - 4 машин. Таким образом, формула для случая n машин одной марки в конкретной позиции где-то в середине стоянки 4·3²·4^n - 4.

Существует 2 позиции n машин одной марки на концах стоянки и n - 3 позиции n машин одной марки где-то в середине стоянки. Окончательная формула 2·4·3·4^n - 3 + (n - 3)·4·3²·4^n - 4.

J. Делимость

Разложим на простые множители числа от 2 до 10. 2 = 2, 3 = 3, 4 = 2², 5 = 5, 6 = 2·3, 7 = 7, 8 = 2³, 9 = 3², 10 = 2·5. Если число делится на все числа от 2 до 10, его разложение на простые множители должно содержать 2 хотя бы в степени 3, 3 хотя бы в степени 2, 5 и 7 хотя бы в степени 1. Так что оно может быть записано как x·2³·3²·5·7 = x·2520. Таким образом, любое число, делящееся на 2520, является делящимся на все числа от 2 до 10.

Существует 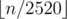чисел от 1 до n делящихся на все числа от 2 to 10. В языке программирования обычно это реализуется как просто деление нацело.

K. Неделимость

Количество чисел от 1 до n, не делящихся ни на какое число от 2 до 10, равно количеству всех чисел от 1 до n (то есть n) минус количество чисел от 1 до n, делящихся на какое-нибудь число от 2 до 10.

Множество чисел от 1 до n, делящихся на какое-нибудь число от 2 до 10, может быть найдено как объединение множества чисел от 1 до n, делящихся на 2, множества чисел от 1 до n, делящихся на 3 и так далее до 10.

Заметим, что множества чисел, делящихся на 4 или 6 или 8, являются подмножествами множества чисел, делящихся на 2, а множества чисел, делящихся на 6 или 9, являются подмножествами множества чисел, делящихся на 3. Таким образом, нет необходимости объединять 9 множеств, достаточно объединить только множества для 2, 3, 5, 7.

Размер множества чисел от 1 до n, делящихся на какое-то из чисел 2, 3, 5, 7, может быть найден с использованием формулы включения-исключения, в которой размеры каждого множества складываются, размеры попарных пересечений множеств вычитаются, размеры пересечений троек множеств складываются и так далее.

Размер множества чисел от 1 до n, делящихся на 2, равен 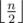, размер множества чисел от 1 to n, делящихся на 2 и 3 равен 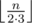и так далее.

Окончательная формула

Деление с округлением вниз в этой формуле в языке программирования обычно выражается просто целочисленным делением.

L. Взлом кода

В этой задаче требуется просто реализация действий, описанных в условии. Однако, есть два подвоха.

Первый подвох заключается в том, что пятая степень пятизначного числа не может быть представлена 64-битным целым числом. Но нам и не нужна пятая степень, нам нужна пятая степень по модулю 10⁵. И операцию mod можно применять после каждого умножения (смотрите разбор задачи A выше).

Второй подвох заключается в том, что требуется вывести пять цифр, а не пятую степень по модулю 10⁵. Разница есть тогда, когда пятая цифра с конца является нулём. Чтобы вывести число с ведущим нулём, можно либо использовать соответствующее форматирование (%05d в printf), либо извлечь цифры числа и выводить их одну за другой.

M. Поворот

Во-первых приведём угол поворота камеры к диапазону [0, 359] градусов. Это можно сделать таким кодом на C++/Java: angle = (angle % 360 + 360) % 360;

Затем получаются следующие случаи:

• [0, 44] градусов — не требуется поворот,
• 45 градусов — поворот 0 или 1 раз для минимального отклонения, минимум 0,
• [46, 134] градусов — требуется один поворот,
• 135 градусов — 1 или 2 поворота для минимального отклонения, минимум 1,
• [136, 224] градусов — требуется два поворота,
• 225 градусов — 2 или 3 поворота для минимального отклонения, минимум 2,
• [226, 314] градусов — требуется три поворота,
• 315 градусов — 3 или 0 поворотов для минимального отклонения, минимум 0,
• [316, 359] градусов — не требуется поворот.

Добавим 44 градуса к полученному углу из диапазона [0, 359] градусов. Код на C++/Java angle = (angle + 44) % 360; После этого диапазоны будут:

• [0, 89] градусов — 0 поворотов,
• [90, 179] градусов — 1 поворот,
• [180, 269] градусов — 2 поворота,
• [270, 358] градусов — 3 поворота,
• 359 градусов — 0 поворотов.

Один особый случай 359 градусов может быть устранён взятием угла по модулю 359. Затем для получения ответа требуется только целочисленное деление на 90. Код C++/Java answer = (angle % 359) / 90;

N. Прогноз

Нет ничего особенного в решении квадратного уравнения, но в этой задаче есть один подвох. Требуется вывести больший корень первым.

Простейший подход состоит в том, чтобы вывести сначала max(x₁, x₂), затем min(x₁, x₂).

Другой подход основан на знаке a.

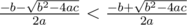для a > 0 и 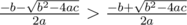для a < 0.

Мы можем разделить все коэффициенты на a, тогда первый коэффициент будет положительным. Однако заметьте, что деление должно быть осуществлено в вещественном типе, а a следует делить последним, в противном случае полученную единицу a / a = 1 нельзя будет использовать для деления b и c.

O. Стрелка

Чтобы получить вектор заданной длины b в направлении заданного вектора (vx, vy), требуется просто нормализовать заданный вектор (поделить его на его длину) и затем умножить на b.

Обозначим 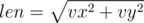, vnx = vx / len, vny = vy / len. Тогда (vnx, vny) — нормализованный вектор, а первая точка стрелки (px + vnx·b, py + vny·b).

Чтобы получить вторую точку стрелки, требуется повернуть нормализованный вектор на 90 градусов против часовой стрелки, затем умножить на половину длины основания треугольника a / 2. Обозначим vlx =  - vny, vly = vnx. Тогда (vlx, vly) — нормализованный вектор, направленный на 90 градусов против часовой стрелки относительно (vnx, vny). Таким образом, вторая точка стрелки (px + vlx·a / 2, py + vly·a / 2).

Третья точка может быть найдена тем же способом, только длина вектора до неё c / 2. Таким образом, третья точка стрелки (px + vlx·c / 2, py + vly·c / 2).

Четвёртая точка может быть найдена добавлением вектора длины c / 2 влево от заданного и вектора длины d противонаправленного заданному. Таким образом, четвёртая точка стрелки (px + vlx·c / 2 - vnx·d, py + vly·c / 2 - vny·d).

Оставшиеся точки симметричны точкам, обсуждавшимся выше, так что они могут быть получены тем же способом, только используя минус перед (vlx, vly) вместо плюса. Таким образом, следующие точки (px - vlx·c / 2 - vnx·d, py - vly·c / 2 - vny·d), (px - vlx·c / 2, py - vly·c / 2), (px - vlx·a / 2, py - vly·a / 2).

P. Площадь звезды

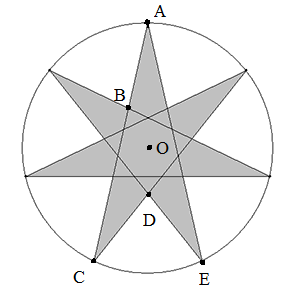
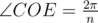, где n — количество лучей звезды, потому что в правильной геометрической звезде все углы между лучами одинаковы.

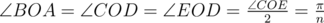из соображений симметрии.

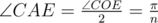, потому что это вписанный угол.

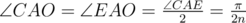из соображений симметрии.

Таким образом, мы знаем, что OA = r 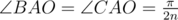и и 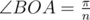. Мы можем найти площадь треугольника AOB, по стороне и двум углам, прилегающим к ней, используя формулу .

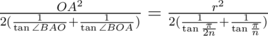Полная площадь звезды равна 2n площадей треугольника AOB из соображений симметрии. Окончательная формула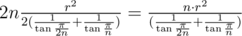

Q. Пирамиды

Объём пирамиды может быть вычислен как 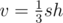где v — объём, s — площадь основания и h — высота, опущенная на основание. Найдём s и h.

Площадь правильного многоугольника, имеющего n сторон длины l_n, может быть найдена следующим образом.

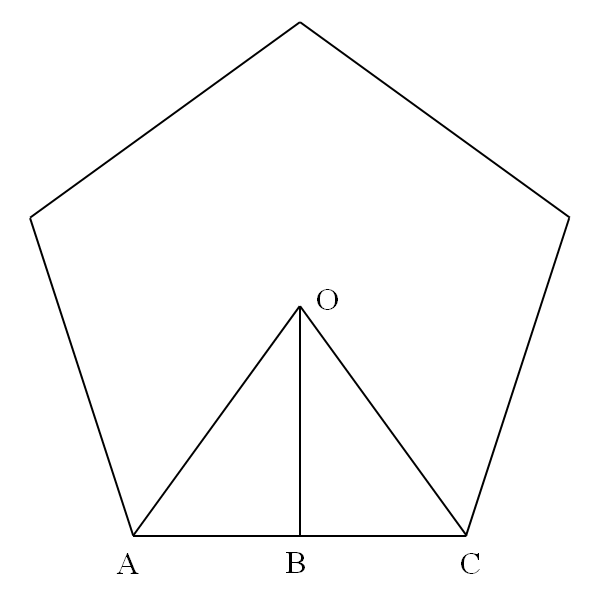
На рисунке выше представлен правильный многоугольник. Точка O — центр многоугольника, все его стороны равны l_n, OB является высотой треугольника AOC. Поскольку многоугольник правильный, OA = OC, треугольник AOC является равнобедренным и 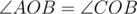и AB = BC, также треугольники AOB и COB являются прямоугольными. Также поскольку многоугольник правильный и может быть представлен как объединение 2n треугольников равных треугольнику AOB, то .

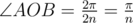Треугольник AOB прямоугольный, так что 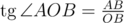, 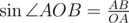. Также 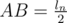. Таким образом, 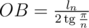и 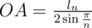. Площадь треугольника AOB равна 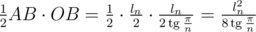. Площадь всего многоугольника .

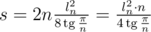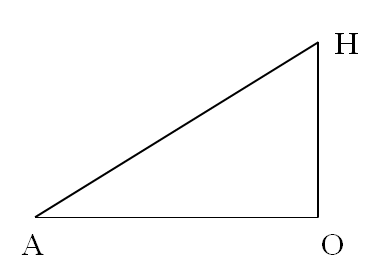
На рисунке выше представлен треугольник с вершинами в точках H — вершина пирамиды, O — центр основания пирамиды и A — некоторая вершина основания. Он прямоугольный. Поскольку все рёбра пирамиды равны, то AH = l_n, и из вычислений выше 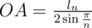. В соответствии с теоремой Пифагора, OA² + OH² = AH². Таким образом, .

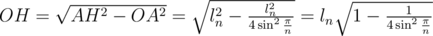Формула объёма одной пирамиды .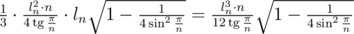

Окончательная формула .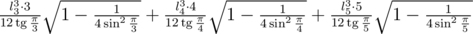

R. Игра

Для поля чётного размера существует выигрышная стратегия для второго игрока. А именно, закрашивать клетку, которая симметрична относительно центра поля клетке, закрашенной первым игроком на предыдущем ходе. После каждого хода второго игрока поле центрально-симметрично, так что какую бы клетку ни выбрал первый игрок, второй всегда может закрасить клетку, симметричную выбранной относительно центра поля.

....  1...  .1..  ....  ....
....  ....  ....  1...  .1..
....  ....  ....  ...2  ..2.
....  ...2  ..2.  ....  ....

Для поля нечётного размера существует выигрышная стратегия для первого игрока. А именно, на первом ходу закрашивать центральную клетку, а дальше закрашивать клетку, которая симметрична относительно центра поля клетке, закрашенной вторым игроком на предыдущем ходе. После каждого хода первого игрока поле центрально-симметрично, так что какую бы клетку ни выбрал второй игрок, первый всегда может закрасить клетку, симметричную выбранной относительно центра поля.

.....  2....  .2...  ..2..  .....
.....  .....  .....  .....  .2...
..1..  ..1..  ..1..  ..1..  ..1..
.....  .....  .....  .....  ...1.
.....  ....1  ...1.  ..1..  .....

Таким образом, для чётных n ответ 2, для нечётных n ответ 1. Одна из возможных формул для задачи .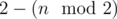

n может быть до 10¹⁸, так что для его ввода требуется по крайней мере 64-битный целый тип.