After getting rank 15 in Codeforces Round 844 (Div. 1 + Div. 2, based on VK Cup 2022 - Elimination Round), arvindf232 has reached Legendary Grandmaster rank with rating 3027. Congratulations!
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3892 |
| 2 | jiangly | 3797 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3588 |
| 6 | ecnerwala | 3557 |
| 7 | Ormlis | 3532 |
| 8 | Benq | 3468 |
| 9 | Radewoosh | 3463 |
| 10 | Um_nik | 3450 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 164 |
| 2 | Qingyu | 159 |
| 3 | -is-this-fft- | 158 |
| 4 | atcoder_official | 157 |
| 5 | Dominater069 | 155 |
| 6 | adamant | 154 |
| 7 | djm03178 | 151 |
| 8 | luogu_official | 150 |
| 9 | awoo | 148 |
| 10 | maomao90 | 145 |
As we all know, Codeforces has a feature that allows users to hide problem tags for unsolved problems. However, when I create a mashup contest, it shows the tags even for unsolved problems.
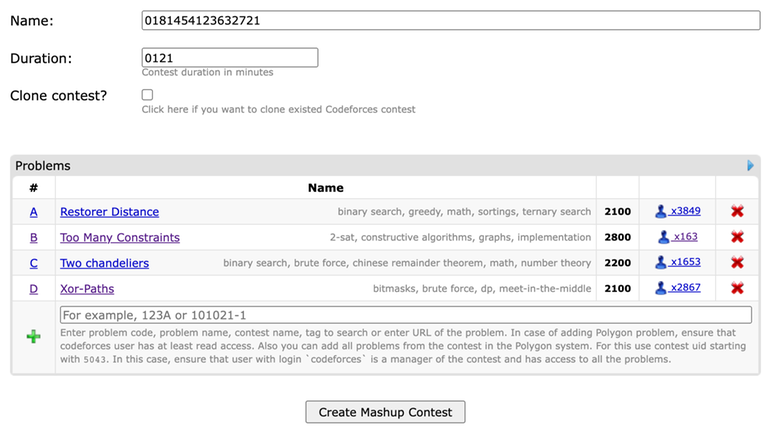
It is a very minor issue, but it would be better if the "hide tags for unsolved problems" also includes hiding tags when adding problems to mashup contests. Just imagine being spoiled by the "ternary search", "2-sat", "meet-in-the-middle" tags right away before reading the problems.
Hello, Codeforces!
I am happy to invite you to Codeforces Round 761 (Div. 2), which will take place on Dec/16/2021 16:35 (Moscow time). The round will be rated for participants with rating lower than 2100. Notice the unusual starting time.
All the problems were authored and prepared by me. The round wouldn’t be possible without these people:
- Artyom123 for excellent coordination and translation of statements.
- KAN for help with round preparation.
- arvindf232, physics0523, SecondThread, Igorbunov, kevinxiehk, generic_placeholder_name, Kotehok3, minhcool, anthony123, Elison, shishyando, SlavicG, Absyarka, erniepsycholone, dbsbs, lomienyeet for testing and valuable feedback.
- Again, arvindf232 and generic_placeholder_name for providing solutions to a problem that are better than the author’s solution.
- Again, kevinxiehk for submitting many different solutions to a problem.
- MikeMirzayanov for great Codeforces and Polygon platforms.
- You, for participating!
You will have 2 hours to solve 5 problems, one of which is divided into two subtasks. One of the problems is interactive, please see the guide of interactive problems if you are not familiar with it.
Wish you good luck and high ratings!
Here is the score distribution: $$$750-1000-1500-(2000-1000)-3000$$$.
The editorial is here: click.
UPD: Sorry but there is a checker bug in problem E. All submissions of problem E will be rejudged soon.
UPD2: Rejudge done, the round remains rated.
Congratulations to the winners (will be updated after system tests):
Div. 2:
- zero8808
- Kon567889
- FakeRainbow_sjy
- zhouziheng
- shengtongtong
- yincheng01
- KennyD
- JavierN
- nebocco
- n0sk1ll
Div. 1 + Div. 2:
First AC:
Problem A: by Kon567889 at $$$2$$$ minutes!
Problem B: by wifiiii at $$$3$$$ minutes!
Problem C: by kidofod at $$$8$$$ minutes!
Problem D1: by Kevin114514 at $$$17$$$ minutes!
Problem D2: by Vercingetorix at $$$28$$$ minutes!
Problem E: by FakeRainbow_sjy at $$$23$$$ minutes!
Thanks for participating, hope you enjoyed the problems! Implementations for the problems are chosen randomly among testers, and I made some changes to their codes (for example, deleted meaningless comment lines). Please do not hesitate to provide feedback in the comments, so I can improve in setting problems next time.
UPD: Sorry but there is a checker bug in problem E. All submissions of problem E will be rejudged soon.
UPD2: Rejudge done, the round remains rated.
Number of FST for rated participants:
Problem A: $$$29$$$
Problem B: $$$90$$$
Problem C: $$$12$$$
Problem D1: $$$4$$$
Problem D2: $$$0$$$
Problem E: $$$6$$$
Number of AK: $$$22$$$
Number of clarifications: $$$85$$$
When is the lexicographically smallest permutation of $$$S$$$ (i.e. the sorted string) not the answer?
If there are no occurrences of a, b or c in $$$S$$$, sort $$$S$$$ and output it.
Else, if $$$T \ne$$$ abc, sort $$$S$$$ and output it.
Else, output all a, then all c, then all b, then the rest of the string sorted.
#include <bits/stdc++.h>
using namespace std;
#define all(x) x.begin(), x.end()
int main() {
int T;
cin >> T;
while(T--) {
string s, t;
cin >> s >> t;
sort(all(s));
vector<int> cnt(26, 0);
for(auto x: s)cnt[x - 'a']++;
if(t != "abc" || !cnt[0] || !cnt[1] || !cnt[2])cout << s << "\n";
else{
while(cnt[0]--)cout<<"a";
while(cnt[2]--)cout<<"c";
while(cnt[1]--)cout<<"b";
for(int i = 3;i < 26; ++i){
while(cnt[i]--)cout<<char('a' + i);
}
cout << "\n";
}
}
}
Originally, the author and two testers' solutions are all wrong, but we didn't notice until the third tester submitted the real correct solution.
There must exist a solution for $$$c=1$$$ under the given constraints.
Key observation: there always exists a solution with $$$c = 1$$$ under the given constraints. We set $$$n \ge 10$$$ because there is no solution when $$$1 \le n \le 5$$$ or $$$n = 7$$$.
Solution 1: Brute force from $$$a = 2, 3, 4, \dots$$$ and calculate the value of $$$b$$$ ($$$b = n - a - 1$$$), then check whether $$$gcd(a, b) = 1$$$. It works, because you will find a prime number $$$p \le 29$$$ such that $$$n-1$$$ does not divide $$$p$$$.
Solution 2: Randomly choose $$$a$$$ and calculate $$$b$$$ ($$$b = n - a - 1$$$). Repeating that for enough times will eventually get you a pair of ($$$a, b$$$) such that $$$gcd(a, b) = 1$$$.
Solution 3: Constructive solution.
When $$$n \equiv 0 \pmod 2$$$, output ($$$n-3, 2, 1$$$).
When $$$n \equiv 1 \pmod 4$$$, output ($$$\left \lfloor \frac{n}{2} \right \rfloor -1, \left \lfloor \frac{n}{2} \right \rfloor +1, 1$$$).
When $$$n \equiv 3 \pmod 4$$$, output ($$$\left \lfloor \frac{n}{2} \right \rfloor -2, \left \lfloor \frac{n}{2} \right \rfloor +2, 1$$$).
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.util.StringTokenizer;
import java.util.Scanner;
public class B {
public static void main(String[] args) {
Scanner fs = new Scanner(System.in);
int T=fs.nextInt();
for (int tt=0; tt<T; tt++) {
int n=fs.nextInt();
for (int target=2; true; target++) {
if (gcd(n-1-target, target)!=1)
continue;
System.out.println(n-1-target+" "+target+" "+1);
if (n-1-target<=1) throw null;
break;
}
}
}
static int gcd(int a, int b) {
return b==0?a:gcd(b, a%b);
}
static void sort(int[] a) {
ArrayList<Integer> l=new ArrayList<>();
for (int i:a) l.add(i);
Collections.sort(l);
for (int i=0; i<a.length; i++) a[i]=l.get(i);
}
}
#include <bits/stdc++.h>
using namespace std;
mt19937 rng((int)std::chrono::steady_clock::now().time_since_epoch().count());
void solve(int tc) {
int n;
cin >> n;
while(1) {
int k = uniform_int_distribution<int>(2, n-2)(rng);
int l = n-k-1;
if(k != l && k != 1 && l != 1 && gcd(k, l) == 1) {
cout << k << ' ' << l << ' ' << 1 << endl;
break;
}
}
}
int main() {
int t;
cin >> t;
for(int i=1; i<=t; i++) {
solve(i);
}
}
#include <bits/stdc++.h>
using namespace std;
void solve(){
int n;
cin>>n;
if (n%2==0) cout<<"2 "<<(n-1)-2<<" 1\n";
else {
int cur=(n-1)/2;
if (cur%2==0) cout<<cur-1<<" "<<cur+1<<" "<<1<<endl;
else cout<<cur-2<<" "<<cur+2<<" "<<1<<endl;
}
}
signed main(){
int t;
cin>>t;
while (t--) solve();
}
1617C - Paprika and Permutation
For any two positive integers $$$x$$$, $$$y$$$ that satisfy $$$x \ge y$$$, what is the maximum value of $$$x \bmod y$$$?
Consider the following input: $$$n = 4$$$, $$$a = [3, 3, 10, 10]$$$. Sometimes, we don't need to do anything to some $$$a_i$$$. When do we have to make operations, and when do we not have to?
Key observation: $$$x \bmod y < \frac{x}{2}$$$ if $$$x \ge y$$$, and $$$x \bmod y = x$$$ if $$$x < y$$$.
Notice that the bigger the $$$x$$$, the bigger the range of values that can be obtained after one $$$\bmod$$$ operation. So, intuitively, we want to assign smaller $$$a_i$$$ to smaller numbers in the resulting permutation.
However, if $$$a_i$$$ satisfies $$$1 \le a_i \le n$$$, we can just leave it there and use it in the resulting permutation (if multiple $$$a_i$$$ satisfy $$$1 \le a_i \le n$$$ and have the same value, just choose one). Let's suppose in the optimal solution, we change $$$x$$$ to $$$y$$$ and change $$$z$$$ to $$$x$$$ for some $$$z > x > y$$$ ($$$x$$$, $$$y$$$, $$$z$$$ are values, not indices). Then changing $$$x$$$ to $$$x$$$ (i.e. doing nothing) and changing $$$z$$$ to $$$y$$$ uses $$$1$$$ less operation. And, if it is possible to change $$$z$$$ to $$$x$$$, then it must be possible to change $$$z$$$ to $$$y$$$. However, if it is not possible to change $$$z$$$ to $$$x$$$, it might still be possible to change $$$z$$$ to $$$y$$$.
Therefore, the solution is as follows: Sort the array. For each element $$$i$$$ in the sorted array:
If $$$1 \le a_i \le n$$$ and it is the first occurrence of element with value $$$a_i$$$, leave it there.
Else, let the current least unassigned value in the resulting permutation be $$$m$$$, if $$$m < \frac{a_i}{2}$$$, we can assign the current element to value $$$m$$$ and add the number of operations by $$$1$$$. Else, output $$$-1$$$ directly.
The solution works in $$$O(n \log n)$$$.
#include<bits/stdc++.h>
using namespace std;
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while(t>0){
t--;
int n;
cin >> n;
set<int> st;
for(int i=1;i<=n;i++){st.insert(i);}
vector<int> rem;
for(int i=0;i<n;i++){
int v;
cin >> v;
if(st.find(v)!=st.end()){st.erase(v);}
else{rem.push_back(v);}
}
sort(rem.begin(),rem.end());
reverse(rem.begin(),rem.end());
int pt=0;
bool err=false;
for(auto &nx : rem){
auto it=st.end();
it--;
int ctg=(*it);
if(ctg>(nx-1)/2){err=true;break;}
st.erase(it);
}
if(err){cout << "-1\n";}
else{cout << rem.size() << '\n';}
}
return 0;
}
1617D1 - Too Many Impostors (easy version)
The weird constraint, $$$\frac{n}{3} < k < \frac{2n}{3}$$$, is crucial.
If you know the index of one crewmate and one impostor, how to find the roles of other $$$n-2$$$ players in exactly $$$n-2$$$ queries?
Query players ($$$1, 2, 3$$$), ($$$2, 3, 4$$$), $$$\dots$$$, ($$$n-1, n, 1$$$), ($$$n, 1, 2$$$). After that, you can surely find out the index of one crewmate and one impostor. Try to find out how.
Key observation: if result of query ($$$a, b, c$$$) $$$\ne$$$ result of query ($$$b, c, d$$$), since $$$b$$$ and $$$c$$$ are common, players $$$a$$$ and $$$d$$$ have different roles. Additionally, if result of query ($$$a, b, c$$$) = $$$1$$$ then player $$$a$$$ is a crewmate (and player $$$d$$$ is an impostor), vice versa.
The first step is to query players ($$$1, 2, 3$$$), ($$$2, 3, 4$$$), $$$\dots$$$, ($$$n-1, n, 1$$$), ($$$n, 1, 2$$$).
If the results of any two adjacent queries (or queries ($$$1, 2, 3$$$) and ($$$n, 1, 2$$$)) are different, we instantly know the roles of the two players that are only included in one query — one is a crewmate, one is an impostor. Since the number of impostors $$$k$$$ and crewmates $$$n-k$$$ satisfy $$$k > \frac{n}{3}$$$ and $$$n - k > \frac{n}{3}$$$, there must be one pair of adjacent queries that are different.
After we know one crewmate and one impostor (let's call them $$$a$$$, $$$d$$$), we can query these two players with each one of the rest of the players. If a query ($$$a, d, x$$$) ($$$1 \le x \le n$$$, $$$x \ne a$$$ and $$$x \ne d$$$) returns $$$0$$$, player $$$x$$$ is an impostor, else player $$$x$$$ is a crewmate.
In total, $$$2n-2$$$ queries are used.
#include <bits/stdc++.h>
using namespace std;
void solve() {
int N;
cin >> N;
int res[N];
for(int i=0; i<N; i++) {
cout << "? " << i + 1 << " " << (i+1) % N + 1 << " " << (i+2) % N + 1 << endl;
cin >> res[i];
}
vector<int> imp;
for(int i=0; i<N; i++) {
if(res[i] != res[(i+1) % N]) {
if(res[i] == 0) imp.push_back(i + 1);
else imp.push_back((i+3) % N + 1);
for(int j=0; j<N; j++) {
if(j != i && j != (i+3) % N) {
cout << "? " << i + 1 << " " << (i+3) % N + 1 << " " << j + 1 << endl;
int r;
cin >> r;
if(r == 0) imp.push_back(j + 1);
}
}
break;
}
}
cout << "! " << imp.size();
for(int x : imp) cout << " " << x;
cout << endl;
}
int main() {
int T;
cin >> T;
for(int i=1; i<=T; i++) {
solve();
}
}
1617D2 - Too Many Impostors (hard version)
Thanks must be given to arvindf232 and generic_placeholder_name for the solution.
Aim to find an impostor and a crewmate's index in $$$\frac{n}{3} + c$$$ queries, with $$$c$$$ being a small constant.
Consider splitting the $$$n$$$ players into groups of $$$3$$$ (and query each group) in order to reach the goal in Hint 1. What is special about the results of the $$$\frac{n}{3}$$$ queries?
Firstly query ($$$1, 2, 3$$$), ($$$4, 5, 6$$$), $$$\dots$$$, ($$$n-2, n-1, n$$$). Due to the constraint $$$\frac{n}{3} < k < \frac{2n}{3}$$$, among the results of these $$$\frac{n}{3}$$$ queries, there must be at least one $$$0$$$ and one $$$1$$$. Now, let's call a tuple ($$$a, b, c$$$) that returns $$$0$$$ a $$$0$$$-majority tuple, and vice versa.
From the easy version, notice that finding one crewmate and one impostor is very helpful in determining the roles of the remaining players. Let's make use of the above observation, and pick one adjacent $$$0$$$-majority tuple and $$$1$$$-majority tuple.
Let's say we picked ($$$i, i+1, i+2$$$) and ($$$i+3, i+4, i+5$$$). Then, we query ($$$i+1, i+2, i+3$$$) and ($$$i+2, i+3, i+4$$$). Among the four queries ($$$i, i+1, i+2$$$), ($$$i+1, i+2, i+3$$$), ($$$i+2, i+3, i+4$$$), ($$$i+3, i+4, i+5$$$), there must be a pair of adjacent queries with different results. From the easy version, we can directly find the index of an impostor and a crewmate.
In all the above cases, we end up knowing an impostor and a crewmate using $$$\frac{n}{3} + 2$$$ queries, including the first step.
You have the index of an impostor and a crewmate now, and around $$$\frac{2n}{3}$$$ queries left.
Consider using at most $$$2$$$ queries to find out roles of each player in each group of $$$3$$$ from Step 1, which should add up to $$$\frac{2n}{3}$$$ queries.
Make use of the information you know about each group (whether it is $$$0$$$-majority or $$$1$$$-majority).
Assume a tuple (group of $$$3$$$) is $$$0$$$-majority. There are $$$4$$$ possibilities of roles of the $$$3$$$ players in the tuple, which are:
impostor, impostor, impostor
crewmate, impostor, impostor (and its permutations)
In each query, reduce half of the possibilities.
It remains to figure out how we can find the roles of the remaining players using $$$\frac{2n}{3}$$$ queries. For each tuple ($$$i, i+1, i+2$$$) queried in the first step, let's assume the tuple is $$$0$$$-majority (because the other case can be solved similarly). Then, there are only four possibilities:
All players $$$i$$$, $$$i+1$$$, $$$i+2$$$ are impostors.
Player $$$i$$$ is a crewmate, players $$$i+1$$$, $$$i+2$$$ are impostors.
Player $$$i+1$$$ is a crewmate, players $$$i$$$, $$$i+2$$$ are impostors.
Player $$$i+2$$$ is a crewmate, players $$$i$$$, $$$i+1$$$ are impostors.
Earlier, we found the index of a crewmate and an impostor, let the index of the crewmate be $$$a$$$ and the impostor be $$$b$$$.
If the tuple ($$$i, i+1, a$$$) is $$$1$$$-majority, either player $$$i$$$ or player $$$i+1$$$ is a crewmate. So, we reduced the number of possibilities to $$$2$$$. To check which player is the crewmate, query it with $$$a$$$ and $$$b$$$ like we did in the easy version.
Else, either there are no crewmates or player $$$i+2$$$ is a crewmate. So, we reduced the number of possibilities to $$$2$$$. To check the role of player $$$i+2$$$, query it with $$$a$$$ and $$$b$$$ like we did in the easy version.
In both cases, we use $$$2$$$ queries for each initial tuple ($$$i, i+1, i+2$$$). So, we used $$$n + 2$$$ queries in total, but we gave you a bit more, in case you used some more queries to find a crewmate and an impostor.
There is one corner case we should handle: if the tuple ($$$i, i+1, i+2$$$) contains $$$a$$$ or $$$b$$$, we can just naively query for each unknown role in the tuple, since we won't use more than $$$2$$$ queries anyway.
#include <bits/stdc++.h>
using namespace std;
int query(int a, int b, int c) {
cout << "? " << a << ' ' << b << ' ' << c << endl;
int r; cin >> r;
return r;
}
void solve(int tc) {
int n; cin >> n;
int a[n+1], role[n+1];
for(int i=1; i+2<=n; i+=3) a[i] = query(i, i+1, i+2);
int imp, crew;
for(int i=1; i<=n; i++) role[i] = -1;
for(int i=1; i+5<=n; i+=3) {
if(a[i] != a[i+3]) {
a[i+1] = query(i+1, i+2, i+3), a[i+2] = query(i+2, i+3, i+4);
for(int j=i; j<i+3; j++) {
if(a[j] != a[j+1]) {
if(a[j] == 0) {
imp = j, crew = j+3;
role[j] = 0, role[j+3] = 1;
}
else {
imp = j+3, crew = j;
role[j+3] = 0, role[j] = 1;
}
}
}
break;
}
}
for(int i=1; i+2<=n; i+=3) {
if(i == imp || i+1 == imp || i+2 == imp || i == crew || i+1 == crew || i+2 == crew) {
for(int j=i; j<i+3; j++) {
if(role[j] == -1) {
role[j] = query(imp, crew, j);
}
}
}
else if(a[i] == 0) {
if(query(i, i+1, crew) == 1) {
if(query(i, imp, crew) == 0) role[i] = 0, role[i+1] = 1;
else role[i] = 1, role[i+1] = 0;
role[i+2] = 0;
}
else {
role[i] = role[i+1] = 0;
role[i+2] = query(i+2, imp, crew);
}
}
else {
if(query(i, i+1, imp) == 0) {
if(query(i, imp, crew) == 0) role[i] = 0, role[i+1] = 1;
else role[i] = 1, role[i+1] = 0;
role[i+2] = 1;
}
else {
role[i] = role[i+1] = 1;
role[i+2] = query(i+2, imp, crew);
}
}
}
cout << "! ";
queue<int> q;
for(int i=1; i<=n; i++) if(role[i] == 0) q.push(i);
cout << q.size();
while(q.size()) {
cout << " " << q.front();
q.pop();
}
cout << endl;
}
int main() {
int T; cin >> T;
for(int i=1; i<=T; i++) solve(i);
}
Translate the problem into a graph problem. What feature of the graph is it asking about?
Draw out the graph, for $$$a_i \le 10$$$. What special property does the graph have?
Any specific algorithm to solve the problem (in Hint 1)?
In graph terms, the problem is as follows: in a graph with infinite nodes, two nodes $$$x$$$ and $$$y$$$ are connected if $$$x + y = 2^k$$$ for some $$$k \ge 0$$$. Among $$$n$$$ special nodes, find the pair of nodes ($$$i, j$$$) with maximum shortest distance.
Here comes the key observation: For any $$$i \ge 1$$$, there exists only one $$$j$$$ ($$$0 \le j < i$$$) such that $$$i + j = 2^k$$$ for some $$$k \ge 0$$$.
The proof is as follows: let's say that $$$0 \le j_1, j_2 < i$$$, $$$j_1 \ge j_2$$$, $$$i + j_1 = 2^{k_1}$$$, $$$i + j_2 = 2^{k_2}$$$. Then, $$$j_1 - j_2 = 2^{k_2} \cdot (2^{k_1-k_2} - 1)$$$. So, $$$j_1 \equiv j_2 \pmod {2^{k_2}}$$$. Since $$$i \le 2^{k_2}$$$, $$$j_1 = j_2$$$.
Then, we realize we can build a graph as follows: add an edge between $$$x$$$ and $$$y$$$ ($$$x, y \ge 0$$$) if $$$x + y = 2^k$$$ for some $$$k \ge 0$$$. Because of the first key observation, the graph must be a tree. We can root the tree at node $$$0$$$.
Our problem is equivalent to finding the pair of nodes which have maximum distance in a tree, which can be solved using the diameter of tree algorithm.
We can't build the entire tree as it has $$$10^9 + 1$$$ nodes. Try to notice something about the depth of the tree, then think of how this could help us solve the problem (by building the tree, or otherwise).
Since $$$0 \le a_i \le 10^9$$$, it is impossible to build the entire tree. A final observation is that: Consider any node $$$v$$$ with degree $$$\ge 2$$$ in the tree, then $$$v > p_v$$$ and $$$p_v > p_{p_v}$$$, therefore $$$v + p_v > p_v + p_{p_v}$$$ ($$$p_x$$$ denotes the parent of node $$$x$$$ in the tree).
Hence the depth of the tree is $$$\lceil \log(max(a_i)) \rceil = 30$$$, since there are only $$$\lceil \log(max(a_i)) \rceil$$$ possible $$$k$$$ ($$$0 \le k < 30$$$) for the sum of two nodes connected by an edge.
So, there are two ways to do it: the first way is to build parts of the tree: only the $$$n$$$ given nodes and the ancestors of the $$$n$$$ nodes. There will be at most $$$O(n \log max(a_i))$$$ nodes, which should fit into the memory limit. The second way is to not build the tree at all, and calculate the LCA (Lowest Common Ancestor) of two nodes to find their distance. Since the depth of the tree is $$$30$$$, LCA of two nodes can be computed by simply checking every ancestor of both nodes.
In both ways, the time complexity is $$$O(n \log max(a_i))$$$.
#include<bits/stdc++.h>
using namespace std;
int f(int x){
for(int i=0;;i++){
if((1<<i)>=x){
return (1<<i)-x;
}
}
}
using pi=pair<int,int>;
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
map<int,pair<pi,pi>> mp;
priority_queue<int> pq;
for(int i=0;i<n;i++){
int v;
cin >> v;
pq.push(v);
mp[v].first=make_pair(0,i+1);
}
while(!pq.empty()){
int od=pq.top();pq.pop();
if((!pq.empty()) && od==pq.top()){continue;}
if(od!=1){
int nx=f(od);
pq.push(nx);
pi send=mp[od].first;
send.first++;
if(mp[nx].first<send){
mp[nx].second=mp[nx].first;
mp[nx].first=send;
}
else if(mp[nx].second<send){mp[nx].second=send;}
}
}
int ra=0,rb=0,rc=-1;
for(auto &nx : mp){
pair<pi,pi> tg=nx.second;
if(tg.first.second==0 || tg.second.second==0){continue;}
if(rc<tg.first.first+tg.second.first){
rc=tg.first.first+tg.second.first;
ra=tg.first.second;
rb=tg.second.second;
}
}
cout << ra << ' ' << rb << ' ' << rc << '\n';
return 0;
}
In some recent CF problems such as 1503B - 3-раскраска, it was mentioned that the interactor is adaptive. Are there any general methods to write adaptive interactors, or does it depend on the problem? Can anyone who has experience writing adaptive interactors share some of your thoughts? Thanks!
Recently, my friends and I wrote a mashup contest. We gave the link to others to register, however I encountered two problems.
Firstly, registration is only open within six hours of contest time. So, when a user gets invited to a mashup, they are not able to register until six hours before contest starts. 
Is there any way to set a custom registration time (e.g. 3 days before the contest)? If there isn't, I think this would be a cool feature to add to mashup contests.
Secondly, after a user is successfully registered, they would receive the pop-up "You have been successfully registered", and they would get redirected to this page. This means that they have to paste the contest link / invitation link again in order to view the contest page (in the format of https://codeforces.me/contests/[6-digit number]). This can be confusing and inconvenient to mashup participants, especially those who encountered this problem the first time. Perhaps they can stay on the page instead of being redirected?
This is not my first time writing a mashup contest (and encountering these problems); I have written a few before.
I have seen this blog talking about a similar issue. However, the registration time problem hasn't been solved, so I would like to hear from your thoughts.
Hello!
I would like to conduct a survey about competitive programming in general, including when you started, how you practice and more.
There are ten questions, and it should not take more than three minutes to finish it. You can click this link to complete the survey.
Thanks for helping!
Update 1: One of the questions, "How confident are you on being a red coder?" now allows decimals (from 1.0 to 5.0) as responses! Also you can submit more than once now.
Update 2: A new question is added: "Which category do you belong to on Codeforces?" (sorry for not adding it previously)
Update 3: The survey will be accepting responses until Thursday, October 22, 2020 at 00:55 (UTC). Results will be out in a few days.
Update 4: The survey is no longer accepting responses. Thank you CF community for helping me fill in the survey! By the way, there are a total of 793 responses.
Update 5: Results are out!
Q1: What is your current age? (Responses: 793)
0-9 (1.1%)
10-19 (42.2%)
20-29 (54.2%)
30-39 (1.1%)
40-49 (0.4%)
50-59 (0.0%)
60 or above (0.9%)
Q2: At what age did you start CP? (Responses: 793)
Most popular responses are from around 12 to 21 years old, in particular 21.8% of the respondents started at age 18, and 20.4% of the respondents started at age 19.
Q3: Which category do you belong to on Codeforces? (Responses: 661)
Newbie or Pupil: 29.3%
Specialist: 17.5%
Expert: 24.4%
Candidate Master: 11%
Master or above: 11.5%
Grandmaster or above: 6.2%
Q4: Which programming language do you use mainly? (Responses: 793)
Most popular responses are C++, Python and Java. 89.8% of the respondents chose C++, 4% and 3.8% chose Python and Java respectively.
Q5: How much time do you spend on CP per week? (Responses: 793)
<1 hour: 4.3%
1-2 hours: 6.8%
3-5 hours: 18.7%
6-10 hours: 26.7%
11-20 hours: 22.8%
21-30 hours: 10.8%
31-40 hours: 4.7%
More than 40 hours: 5.2%
Q6: How do you learn algorithms or data structures in general? (Responses: 793)
Online judges: 60.9%
Books: 40.2%
Tutorial sites: 59%
Reading editorials of problems: 22.1% (I added this at a later time so the actual percentage may be larger)
Other popular responses: YouTube, CF blogs, College courses, CP algorithms, Mentors, Friends, Codeforces EDU
Q7: Which online judges / contest sites / coding platforms do you use? (Responses: 793)
Codeforces: 97%
AtCoder: 62.5%
CodeChef: 56.9%
LeetCode: 27.4%
HackerRank: 24.1%
HackerEarth: 20.3%
UVa: 12.1%
TopCoder: 6.9%
CodinGame: 3%
Other popular responses: USACO, Local judges, CSES, SPOJ, LightOJ, oj.uz, CS Academy, DMOJ, Timus
Q8: What is your attitude towards getting top 100 in a Codeforces Round? (Responses: 792)
My hard work paid off: 53.4%
Oh I just got lucky: 43.7%
I'm so pro: 6.6%
I always get top 100, so it's nothing special to me: 3.3%
Q9: How confident are you on being a red coder/LGM? (Responses: 793)
Most popular responses: around 3.8 to 5
Least popular responses: 1
Q10: If you are a student, is schoolwork or CP more important? (Responses: 703)
1 — Schoolwork is more important
5 — CP is more important
1: 5%
2: 8.4%
3: 18.3%
4: 31.3%
5: 37%
I have found out that two contestants of the round aditi_gupta07 and aviban99 had almost identical codes. Here are their submissions:
Problem A: (89928617, 89935523)
Problem B: (89944498, 89950768)
MikeMirzayanov please look into this incident and take necessary actions against them.
| Name |
|---|










