Hi everyone!
Some days ago, I confronted to a hard problem and I could not solve it. Can you help me?
The problem was: Given a and n(1 <= a, n <= 1000). And b = (a ^ a) ^ (a ^ a). And return b mod n.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
Hi everyone!
Some days ago, I confronted to a hard problem and I could not solve it. Can you help me?
The problem was: Given a and n(1 <= a, n <= 1000). And b = (a ^ a) ^ (a ^ a). And return b mod n.
| Название |
|---|



Auto comment: topic has been updated by VIIIIIIVX (previous revision, new revision, compare).
Use a^phi(n) is 1 mod n. Find a^a mod n, and a^a mod phi(n).
This is valid only if a and n are co — prime,and he has not mentioned so in the blog
True that. If that's not true, then that's some real trouble. Maybe this helps in that case.
Incase a, n are co-prime, I guess this will work.
You can use Euler's Theorem for xy % n even when gcd(x, n) ≠ 1. This requires that the residue used in the exponentiation is equal or bigger than the highest power of the prime powers shared by x and n. So in such case, find y % φ(n) until the value is the smallest value greater or equal to the highest power of the prime factors shared by x and n.
Having said this, in above case the highest shared power is ≤ 10. So calculations then can fit in long long.
A simple way is to compute the values 1, a, a2, a3, ... modulo n until you find a loop. Due to non-coprimeness issues, it may not end in 1, so it has the so-called ρ structure (a tail and a cycle). Still, we know the start of the cycle and its period, so we can reduce the exponent modulo this period.
So now we have to compute the exponent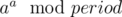 . This can be done straightforwardly or using fast exponentiation.
. This can be done straightforwardly or using fast exponentiation.
Oh yes yes, thans a lot!