Hey Guys ! This is my first education blog , now in Codeforces, acc to me , we don't use so much pointers so like if there is some tree question then we would directly convert it into graph or use graph algos to do it. So I studied on trees for like 3-4 days and I really want to share my knowledge with you all genius and smart people.
PS: I just new to this , if I did any mistake then please correct me :)
POINTER TO POINTER METHOD IN TREES
Now I realized that many my friends do questions in return type of recursive function like if you are inserting or deleting the node or changing the edges then you would use return type as when we send this argument node * root then we are not actually sending root , we are sending the copy of root or maybe you can say that we are sending the another pointer which is pointing to the same node which the root was pointing then I thought it would be easy to do questions if we actual send the real root , why do we have to send copy , if we able to send the real root then we could able to do all questions in void , so no need to return type so for that use
node* &root so by this we could able to send the real root or you can say we have made a pointer which is pointing the root pointer/ storing address of root pointer.
BST
Recursive Part
Now I used GeeksforGeeks for this (those 20 questions on BST trees were awesome!)
1) Print Postorder traversal from the given pre and inorder traversal
Root is always the first element in pre-order transversal and it is last element in post-order traversal Now the challenging thing is that to find the boundaries of the left and right subtree so in INORDER all elements left to the root are left elements and right to the root are right elements Now,in pre , all elements after the index of the root are elements of right subtree and all elements before the index of the root [including the index of root in inorder but excluding the first element of pre order] are elements of the left subtree
Now let — Inorder be : DBEAFC — preorder be: ABDECF
Now A is root so DBE in inorder will be left subtree so BDE is also left sub tree from pre-order
Now we are here — Inorder : DBE — Preorder : BDE
now the root is B (as first element of the preorder is root so all left elements before B are it's left element now then
- Inorder :D
- pre-order :D
so single element so print it [as we are at the left leave node now] so now B's right element would be called
- Inorder :E
- preorder :E
now single element print it Now we traverse came back to B then print B now DEB is printed till now same do for FC in order as they are right subtree should I explain the FC part also ? okk
so — Inorder :FC — pre-oder :CF
now C is root then no right element and only F left element , so now DEBFC now we traversed back to A again so final print is DEBFCA
Notice some imp point: You see that in this recursion we made root every node first A then B->D->E->C->F so is this same order in pre-order???
ohh yes! it is !
so we will use this thing to implement in our code
CODE
Below is the implementation.
Just try urself!first :)
Now this is o(n^2) algorithm
Let's optimize it to o(n) algo As we know that in BST every node is Unique value so why we are doing searching , we can store all values in MAP and after that then we can find the element in o(1) time
so instead of making search function use map
for (int i = 0; i < n; i++)m[in[i]] = i; // stored all indexes of the unique values2) Tree from pre-order and Inorder Traversal
Hint: use previous algo to do it :)
CODE
[when PreIndex reach Inorder[preorder[0]] then left subtree would be formed of main root and from Inorder[Preorder[0]]+1 right subtree will start forming ]
2.1) Tree from post-order and In-order
Now , for like
Inorder : 42513 Post-order : 45231
and actual tree is
Now notice one thing root is always at end so we will able to find the root from the end of the post-order and end-1 of postorder contains the root of right subtree, so as In pre-order we used to go from 0 to n-1 as we used to solve left first then right as in pre-order first left comes after root [remember center-left-right] Now here before root, right comes[left-right-center/root] so we will go from n-1 to 0 and solve first right then left!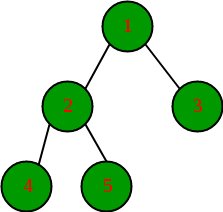
CODE
3)Finding the kth smallest element
vector v;
void inorder(TreeNode* &root, int k)
{
if(root==NULL) return;
inorder(root->left, k);
v.push_back(root->val);
if(v.size()>=k) return;
inorder(root->right, k);
}
4) 2 sum Binary Tree
Given a binary search tree T, where each node contains a positive integer, and an integer K, we have to find whether or not there exist two different nodes A and B such that A.value + B.value = K.
PLEASE TRY FIRST THEN SEE THE CODE :)
CODE
5)How to find that is the Traversal is Valid or not?
Now like we have given a preorder traversal A, of a Binary Search Tree. Find if it is a valid preorder traversal of a BST.
:
code
{note : here we are traversing on pre-order}
6)Convert sorted Array to Balanced BST
:
7)Recover Binary Search
Two elements of a binary search tree (BST) are swapped by mistake. we have to tell the 2 values swapping which the tree will be restored.
8)Inorder Traversal of Cartesian Tree
Cartesian tree : is a heap ordered binary tree, where the root is greater than all the elements in the subtree
NON recursive part in stacks
Implementing Traversals using Stacks
In-order (**Time Complexity is o(n) and o(h) space where h is max height**)
LINK FOR THE INORDER TRAVERSAL STACK METHOD
Point : [first we go till down left then we print the value then we make curr to to it's right if it's right is NULL like in case of 4 then again pop the stack and do with 2 now it's curr->right is not NULL now do same approach of go to left ]
Pre-order(**Time Complexity is o(n) and o(h) space where h is max height**)
In this everything is same as In-order it is just here we would print the root when we are going to add it and traverse to it's left and rest is same
CODE
Least Common Ancestor
Binary Search Tree
IT will help you for LCA in BST
Now if both nodes are one side then go to that side , but when the both nodes are apart then break at that node(U) which separate them and that node(U) will be the answer as after that node(U) , no node will contain both the required nodes.
Now if the LCA is one of the the required node like in this case, so in this it means there is no node (U) which cover both nodes, so the node(one of the required nodes) with greater height than other will be answer , like here 8 for 8 and 14
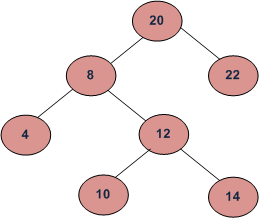
In this Backtracking was involved.
Extra I really liked this question , you can try this !
Number of Binary Search Trees from the Given length of Preorder sequence
one more point
Thank you so much guys! for reading this blog!!!









