Hi everyone!
Let's continue with learning continued fractions. We began with studying the case of finite continued fractions and now it's time to work a bit with an infinite case. It turns out that while rational numbers have unique representation as a finite continued fraction, any irrational number has unique representation as an infinite continued fraction.
Part 1: Introduction
Part 2: Properties and interpretation









 and not
and not 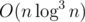 as it was before.
as it was before.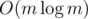 as
as 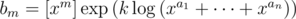 .
. 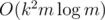 if I'm not mistaken. Can anybody suggest any faster algorithm?
if I'm not mistaken. Can anybody suggest any faster algorithm?
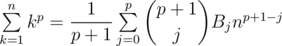
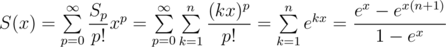
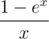 and multiplying it with
and multiplying it with 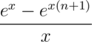 . Enjoy your power sums without Stirling and/or Bernoulli numbers!
. Enjoy your power sums without Stirling and/or Bernoulli numbers!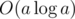 .
.

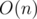 вместо заявленных
вместо заявленных  .
.  correspond to segment
correspond to segment 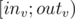 and the path from
and the path from 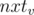 ) will be
) will be 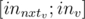 subsegment which gives you the opportunity to process queries on pathes and subtrees simultaneously in the same segment tree.
subsegment which gives you the opportunity to process queries on pathes and subtrees simultaneously in the same segment tree.
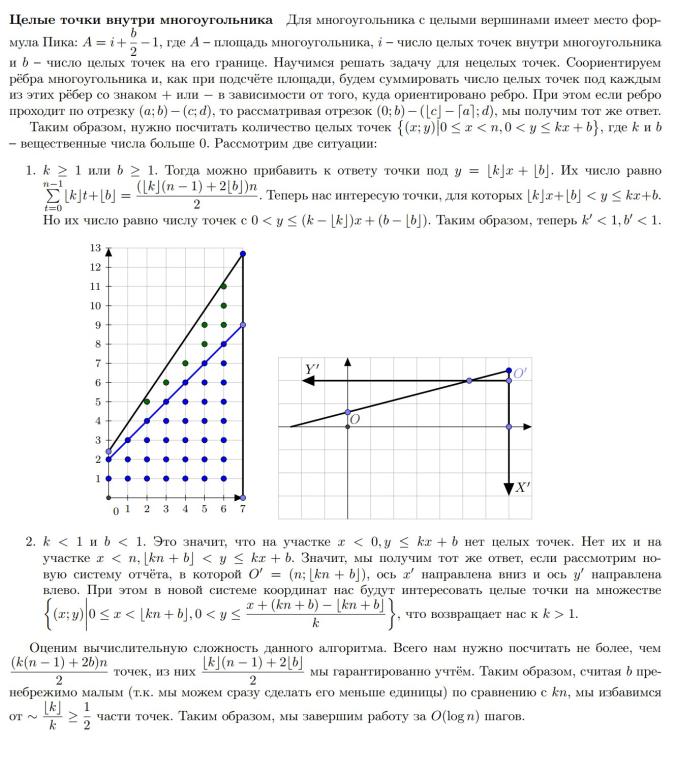
 ?
?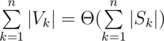 ? Can you prove it or make a counter-example?
? Can you prove it or make a counter-example?
