adamant's blog

Question about suffix automaton/tree
By adamant, history, 8 years ago, In English

Hi everyone!

As you may know, it is possible to build a suffix automaton for a set of strings as well as suffix tree consisting of all suffixes of strings from the set. Question is as follows: for each string Sk consider set Vk of vertices/states of tree/automaton that corresponds to the substrings of Sk. Is it true that 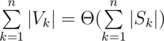? Can you prove it or make a counter-example?

  • Vote: I like it
  • +46
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What prevents |Vk| from being always Θ(|Sk|) for suffix trees?

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 3   Vote: I like it +3 Vote: I do not like it

    We can take Sk, k > 1 as set of substrings of S1. Then |V1| will be Θ(|S1|2).

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Set of prefixes should have the same effect. Every |Vk| is Ω(|Sk|2) then, right?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Seems to be correct, cool! Then for total length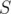 this sum will be 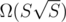and 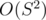. Can you improve the boundaries now?

        → Reply