Hi there! Imagine you're participating in codechef long challenge and you see a problem from chemthan asking you to calculate some sums of powers like 1p + 2p + ... + np for all p from 0 to k. You immediately understand what's going on here and take Faulhaber's formula from your wide pants, do ya? Just take a look at it!
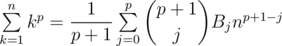
Beautiful, right? Wrong! This formula is dumb and it's hard to understand and remember! Why would you ever think about Bernoulli's number on any contest which lasts less than a week? And what the hell are those Bernoulli numbers?! Here is what you should do:
Let Sp = 1p + ... + np. Consider its exponential generating function (EGF):
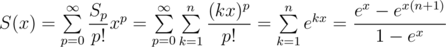
Now you can simply find S0, ..., Sk by finding inverse series for 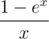 and multiplying it with
and multiplying it with 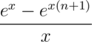 . Enjoy your power sums without Stirling and/or Bernoulli numbers!
. Enjoy your power sums without Stirling and/or Bernoulli numbers!
Exercise: Solve this problem in 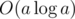 .
.
P.S. Yes, you basically perform the same calculations as in Faulhaber's formula, but now you hopefully understand what you're doing.






