
Всем привет!
Я надеюсь, никто не забыл, что каждый год перед ICPC World Finals проводится небольшое соревнование ICPC Challenge. Разумеется, этот год не будет исключением. Если вдруг кто-то не знает об этом, то ICPC Challenge — это дополнительный двухнедельный контест по программированию искусственного интеллекта в какой-нибудь игре для финалистов чемпионата мира по программированию ACM-ICPC. Победитель определяется по системе double-elimination tournament, и будет объявлен на одном из мероприятий Финала.
ICPC Challenge 2013 начался несколько дней назад (точнее 3 июня), и сейчас я хочу торжественно объявить, что он был подготовлен небольшой командой из Baylor University, North Carolina State University и Saratov State University, который я представляю! Мы приготовили для вас новое задание, которое носит название CodeRunner.
Немного об игре
Задание на 2013 ICPC Challenge, CodeRunner, представляет собой игру на прямоугольном поле, которое выглядит как на картинке ниже. Красный и синий игроки перемещаются по полю, собирают золото, убегают от врагов, которые двигаются по полю. Каждый игрок может перемещаться вбок, карабкаться вверх и спускаться вниз по лестницам, а кроме того разбивать кирпичи, которые находятся на игровом поле. Кирпичи могу восстанавливаться через некоторое время после разрушения.

Приятная новость
Но самая главная новость заключается в том, что в этом году в соревновании могут участвовать все желающие! Параллельно с основным ICPC Challenge для финалистов чемпионата мира, мы запускаем новое соревнование Open ICPC Challenge. Каждый может принять в нем участие и сразиться против лучших команд по программированию в игре CodeRunner!
Вы можете найти больше информации тут и тут.
Мы будем рады видеть каждого из вас :)
Удачи!









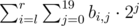 что равно
что равно 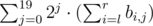 , то есть мы можем перебрать номер бита
, то есть мы можем перебрать номер бита 

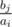 . Затем запустим этот алгоритм еще раз, таким образом найдем искомое количество пар, где достигается максимальное значение.
. Затем запустим этот алгоритм еще раз, таким образом найдем искомое количество пар, где достигается максимальное значение.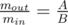
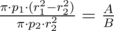
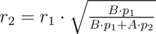
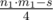 . Мы можем перебрать одну из сторон уголка, найти вторую, проверить что все ограничения выполняются, и за каждую найденную пару сторон прибавить к ответу функции по
. Мы можем перебрать одну из сторон уголка, найти вторую, проверить что все ограничения выполняются, и за каждую найденную пару сторон прибавить к ответу функции по 

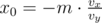 . Теперь допустим
. Теперь допустим 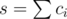 . Тогда несложно понять, что если мы всех этих роботов упакуем так, чтобы лишь
. Тогда несложно понять, что если мы всех этих роботов упакуем так, чтобы лишь 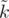 из них ехало самостоятельно, а остальные были вложены в другие роботы, то еще у нас останется
из них ехало самостоятельно, а остальные были вложены в другие роботы, то еще у нас останется 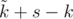 свободных слотов для других роботов.
свободных слотов для других роботов.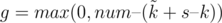 . Таким образом, нам надо найти среди всех роботов с
. Таким образом, нам надо найти среди всех роботов с 
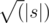 , проверка каждого работает за
, проверка каждого работает за 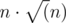 , где
, где 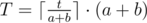
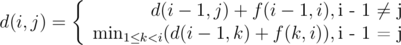
 , где
, где 
