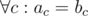Codeforces Round #101 (Div. 2) Разбор Задач.

#	User	Rating
1	tourist	4009
2	jiangly	3821
3	Benq	3736
4	Radewoosh	3631
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3388
10	gamegame	3386

#	User	Contrib.
1	cry	164
1	maomao90	164
3	Um_nik	163
4	atcoder_official	161
5	-is-this-fft-	158
6	awoo	157
7	adamant	156
8	TheScrasse	154
8	nor	154
10	Dominater069	153

141A - Amusing Joke

It was enough for solving this problem to calculate for each letter: a_c - amount of occurrences of letter c in first and second strings in input, b_c - amount of occurrences of letter c in third string in input. If $\text{[math]}$ the answer is "YES" else "NO".

141B - Hopscotch

Let's bust the "level" 0 ≤ i ≤ 10⁶, in which assumedly the stone could hit. Let’s find the minimal number of square on this level. Then we can understand, how many squares there are on this level: one or two. Then we check with one or two ifs (if on this level two squares) if the stone is in corresponding square or not. If the stone is inside then output the answer. If we didn't find any square, where the stone is, output "-1".

141C - Queue

Let's sort the pairs (name_i, a_i) by ascending of a_i. If there is an index i: 0 ≤ i < n that a_i > i, then answer is "-1". Otherwise the answer exists. We will iterate through the array of sorted pairs from left to right with supporting of vector of results res. Let on the current iteration a_i = n - i, then we must transfer the current man in the position a_i. It can be done in C++ with one line: res.insert(res.begin() + a[i], man);

141D - Take-off Ramps

Let's generate the weighted directed graph of all ramps. The graphs' vertexes are the important points on the line Ox, there are points: 0, L, x_i - p_i, x_i + d_i. The graphs' edges are the possible ramp jumps: transfer from point x_i - p_i to point x_i + d_i or transfer from vertex in neighboring vertexes (neighboring means that we get the next and previous important points on the line). The weights of these edges are correspondingly p_i + t_i and x_v + 1 - x_v, x_v - x_v - 1. We must note that in the transfers we can't get in the negative part of Ox, and we must delete this transfers.

Then we must find and output the shortest path in this graph from vertex 0 to L. This can be done, for example, with Dijkstra's algorithm for the sparse graphs.

141E - Clearing Up

In this problem we must find the minimum spanning tree, in which the half of edges are marked with letter 'S'.

There are n - 1 edges in this tree, because of it if n is even then the answer is "-1".

Let's delete from the given graph all S-edges. And there are cnt components in obtained graph. For making this graph be connected we must add cnt - 1 edges or more, that's why if cnt - 1 > (n - 1) / 2 the answer is "-1". Then we find cnt - 1 S-edges, that we must add to the graph, so that it become connected. If cnt - 1 < (n - 1) / 2 then we will try to add in this set of edges another S-edges, so that the S-edges don't make circle. We must do all of this analogically to Kruskal's algorithm of finding a minimum spanning tree. If we could get a set of S-edges of (n - 1) / 2 elements, that there are exactly cnt - 1 edges and no S-circles, then the answer exists, Then we must add to this set (n - 1) / 2 M-edges, that forms with our set of edges the minimum spanning tree, it must be done analogically with Kruskal's algorithm.

Comments (16)

Show archived | Write comment?

DamianS

13 years ago, # |

It would be nice to see a proof why does such an algorithm work for problem E.

→ Reply

niyaznigmatul

13 years ago, # ^ |

It's easy to prove as well.

If this algorithm outputs -1 then there are three ways:

1) odd number of edges in the tree, that works correct

2) ( $\text{[math]}$ ) then there doesn't exist $\text{[math]}$ edges of first color that doesn't make a cycle

3) You can't connect the graph with second type of edges, then you can't connect it at all, so it's correct

So if output is -1, then answer doesn't exist.

Why if output is not -1, then answer exists and correct?

So you get cnt components, then you add cnt - 1 edges of second type, then you just add remaining second type edges (all counted as $\text{[math]}$ ), that all second type edges doesn't make a cycle.

But you say there are the cycles that contains, two types of edges, when cycle appears you just remove one first type edge from the cycle. So the graph that you built is correct and it contains everything asked in the problem statement.

This is not complete, there is also another situation when you output -1. Let's say: we added all M-edges and got a spanning tree (none of your 1), 2), 3) conditions applies), but there is still a possibility for the answer to be -1.

Ah.. Yes

I have to change 3)

You can't connect graph with second type of edges or you can't get $\text{[math]}$ second type of edges that doesn't make a cycle.

Then it's -1 and it's correct.

Ok, but it is not clear if the algorithm checks this condiction correctly. I mean it chooses some S-edges which make the M-forest into a spanning tree and then until there are less then (n-1)/2 s-edges it adds new s-edges in such a way that no s-cycle appears. But why the success of such a procedure doesn't depend on the chosen (at the beginning) s-edges? Etc., etc. It's not as obvious as you say.

OK, what you say it's mistake when answer exists, but algorithm doesn't find it. And it's 3). (it outputs -1)

Firstly, if you can't connect the components, but the answer exists.

So if you add all the s-edges, then the components will stay the same, so if you can't connect the graph, then you can't connect it at all.

Secondly, if you have $\text{[math]}$ m-edges, that doesn't make a cycle, you certainly will find and add them, because you firstly connect components, it doesn't matter what edges to connect with, since it's matroid (there will always exist and edge, that doesn't make a cycle, if there's larger set of edges, that doesn't make a cycle)

so you just add the edges one by one until there are $\text{[math]}$ m-edges. so you get m-edges set and s-edges set, you can remove some edges from s-edges set to get the tree.

Ok, now it looks much better. The keyword here is "matroid". Thank you.

looool

can someone explain solution for problem C ?

sorry, but it is very unclear from the tutorial

noxwell

← Rev. 2 →

OK, lets do it in English.

Make vector q, where we will place people in right order, that will be an answer. Sort input people by decreasing of a, give them height from n to 0, place them in array m and go from begining of this array to the end. When m[i].a=0, just place them in vector q by decreasing of h. Notice, that they are the highest people. It means, that if we place some element in vector q on place ai, before him will be ai people, higher than he, that meets the problem.

superstar

There are n - 1 edges in this tree, because of it if n is even then the answer is "-1".
That would normally be correct, but here we can have roads that start and end at the same hut, so we can add such a road without changing the connectivity, can't we?
2 2
1 2 S
1 1 M
For this case, isn't the solution to clear both roads?

flashmt

← Rev. 4 →

~~"between any two huts should exist exactly one simple path along the cleared roads". That case results in 2 paths from 1 to 2. Hence, we can't clear roads which connect the same hut.~~

UPD: I misunderstood it. Your opinion seems correct based on the problem statement.

ItsLastDay

I think, there is a path 1-1 which is not simple, therefore answer is -1.

There are always paths that are not simple: 1-2-1. Edges are bidirectional

The problem statement states that there is exactly 1 simple path. 1-2-1 is not simple so we don't need to count it.

Ye, that was my point. 1-2-1 and 1-1 are not simple paths so they do _not_ invalidate the conditions.

Either the author of the problem meant to say something else or the official solution is just wrong. I am betting on the second possibility.

When I read that you can have a road starting and ending at the same hut, I was sure that this was added just to make it a little more tricky. Otherwise, what's the point?

gzz

8 years ago, # ^ |

I think the roads which begin and end in the same hut are useful to adjust one nearly right answer to a right one.

for example, if I got S=10 M=9, and one road 2->2 is M, I can choose this road so that S=M=10.

between any two huts should exist exactly one simple path along the cleared roads

and the rule above is satisfied, too. because 2->2 is never used, for when it's used nd 2 appeared twice. so whether to choose 2->2 is not important.

To conclude, the solution for problem E is wrong || the problem statement needs change.

Gerald's blog