It is always optimal to add the smallest integer which is not already in the array.

The number of operations will never exceed $$$\sqrt{2 \cdot s}.$$$

Based on the first hint, the final array will be equal to $$${v_1,v_1,\ldots, v_n} \cup [1,x]$$$, for some $$$x$$$.

Hint 4: How can we find the value of $$$x$$$ faster than $$$O(\sqrt{s})$$$?

Lemma: The number of operations will never exceed $$$\sqrt{2 \cdot s}$$$.

Since we need to maximize the final length of the array, it is always optimal to add the smallest integer which is not already present in $$$a$$$.

The naive implementation of this idea has a runtime complexity of $$$O(n \cdot \sqrt s)$$$, although this can be easily optimized to $$$O((n+ \sqrt s)log(n))$$$, if binary search is used to check whether the new elements are already present in $$$a$$$.

The optimal solution has a runtime complexity of $$$O(N log S)$$$. Based on hints $$$3$$$ and $$$4$$$, we can find the value of $$$x$$$ with binary search. For some $$$x$$$, the sum of the elements in $$$a$$$ will be equal to $$$sum(x)=\frac{x\cdot(x+1)}{2}+\sum_1 v_i$$$, where $$$\sum_1 v_i$$$ is the sum of the elements greater than $$$x$$$.

Since the sum of elements $$$sum(x)$$$ is a monotonous function, we can use binary search on the interval $$$[1,\sqrt{2 \cdot s}]$$$ to find the exact value of $$$x$$$.

Final time complexity: $$$O(N log S)$$$

The numbers are printed in ``layers''.

Try to represent the layers as a binary tree.

To better understand the solution, let's consider $$$n=12$$$. The final array is the BFS traversal starting from the root of the following binary tree:

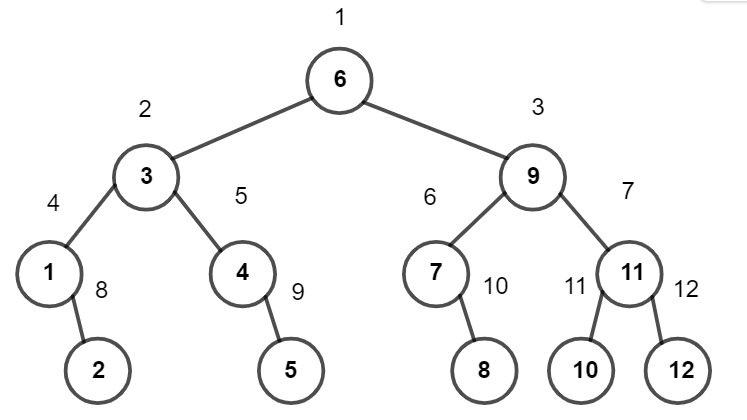
This binary tree was generated by starting with the root $$$m=\lfloor \frac{n+1}{2} \rfloor=6$$$. Each node $$$m=\lfloor \frac{l+r}{2}\rfloor$$$ has up to two children: $$$m_1=\lfloor \frac{l+(m-1)}{2} \rfloor$$$ and $$$m_2=\lfloor \frac{r+(m+1)}{2} \rfloor$$$.

If our given integer $$$k$$$ is in a complete layer, then we can employ a binary search-type algorithm to find the position of $$$k$$$:

l = 1, r = n, position = 1, visited_nodes = 1
while(visited_nodes<=n){
    m = (l + r) / 2

    if(k==m){
        print position
        return
    }
    
    if(k<m) position = position * 2
    else position = position * 2 + 1

    visited_nodes = visited_nodes * 2 + 1
}

This algorithm has the added benefit of not printing anything if $$$k$$$ is not in a complete layer. In this case, the position of $$$k$$$ in the last layer can be determined from $$$position$$$, although this isn't as straightforward. If the binary tree were complete, then the position of $$$k$$$ in the last layer would be $$$position-\frac{\text{visited_nodes}-1}{2}$$$, since there are $$$\frac{\text{visited_nodes}-1}{2}$$$ nodes on the other layers, all of which will be printed before $$$k$$$.

By looking at the missing nodes from the binary tree for $$$n=12$$$, one may make the crucial observation that the general case position for $$$k$$$ in the last layer is equal to $$$k-(position-\frac{\text{visited_nodes}-1}{2})$$$.

In conclusion, the final position for $$$k$$$ will be $$$k-(position-\frac{\text{visited_nodes}-1}{2})+\frac{\text{visited_nodes}-1}{2}=k+\text{visited_nodes}-position-1$$$.

Time complexity per testcase: $$$O(log n)$$$