977D — Divide by three, multiply by two
We can see that all numbers in given sequence are distinct. since all numbers in sequence are of the form
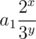 . Hence if ai = aj then
. Hence if ai = aj then 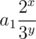 =
= 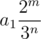

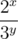 =
= 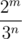
 2x - m = 3y - n which is not possible because any power of 2 will be an even number and any power of 3 will be an odd number.
2x - m = 3y - n which is not possible because any power of 2 will be an even number and any power of 3 will be an odd number.if there exists
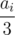 in sequence then 2 * ai can not be in sequence and vice versa. We can prove it using contradiction. Suppose there is a number ai such that both
in sequence then 2 * ai can not be in sequence and vice versa. We can prove it using contradiction. Suppose there is a number ai such that both 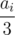 and 2 * ai exists in sequence. by little bit of tricks this
and 2 * ai exists in sequence. by little bit of tricks this 
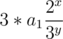 =
= 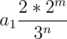 , this again is not possible by same argument as above, we just have to change the order of exponents.
, this again is not possible by same argument as above, we just have to change the order of exponents.Hence for each ai in sequence we see if
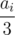 or 2 * ai is present(remember that only one of them can be present). Now if there is any ai such that both
or 2 * ai is present(remember that only one of them can be present). Now if there is any ai such that both 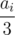 and 2 * ai is not in sequence then this should be an. if there is any such ai that for all 0 ≤ j ≤ n:
and 2 * ai is not in sequence then this should be an. if there is any such ai that for all 0 ≤ j ≤ n:  ≠ ai AND 2 * ai ≠ ai, then this is a1.
≠ ai AND 2 * ai ≠ ai, then this is a1.Once you have got a1, you keep on producing sequence just by doing binary search for
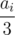 and 2 * ai (remember only one of them is present so once you find it you print it).
and 2 * ai (remember only one of them is present so once you find it you print it).






