Here's the problem (IMO 2013 Problem 1): Assume that k and n are two positive integers. Prove that there exist positive integers m1, ... , mk such that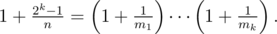 
Think:
Spoiler 0
Spoiler 1
Spoiler 2
Spoiler 3
Spoiler 4
Mega Spoiler
Here's a generalization, which is much easier once you've found the segtree solution to the above problem. Assume that k and n are two positive integers. Prove that there exist positive integers m1, ... , mk such that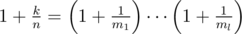 
, where l is an integer and l ≤ log2(k) + 1.
Challenge: Implement the two variants of the problem. In the generalization, you are given k and n, and you are required to output an array that consists of m1, m2, ..., ml.
