Here's the problem (IMO 2013 Problem 1): Assume that k and n are two positive integers. Prove that there exist positive integers m1, ... , mk such that 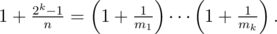
There is an inductive proof, but some people have issues with induction because they give no insight.
Another solution path is just plugging in formulas and if they're right it generally works out. But there may beno hints as to where the formula came from. My proof and intuition behind my solution has a lot of similarities with how segment trees function.
Think:
Here's a generalization, which is much easier once you've found the segtree solution to the above problem. Assume that k and n are two positive integers. Prove that there exist positive integers m1, ... , mk such that 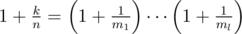 , where l is an integer and l ≤ 2 × ceil(log2(k / 2 + 1)).
, where l is an integer and l ≤ 2 × ceil(log2(k / 2 + 1)).
Challenge: Implement the two variants of the problem. In the generalization, you are given k and n, and you are required to output an array that consists of m1, m2, ..., ml.



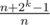 to a range
to a range 

