665A - Buses Between Cities
Задачу предложил Сергей Эрлих unprost.
Рассмотрим интервал времени, когда Симион будет находиться на трассе строго между городами (x1, y1), (x1 = 60h + m, y1 = x1 + ta). Переберём встречный автобус. Пусть (x2, y2) — это интервал времени, когда встречный автобус будет находиться строго между городами. Если пересечение этих интервалов (x = max(x1, x2), y = min(y1, y2)) не пусто, то Симион посчитает этот автобус.
Сложность: O(1).
665B - Shopping
Задачу предложил Ayush Anand JeanValjean01.
В этой задаче нужно было сделать ровно то, что написано в условии. Никаких хитростей и подвохов.
Сложность: O(nmk).
665C - Simple Strings
Задачу предложил Zi Song Yeoh zscoder.
Для решения этой задачи есть два подхода: жадность и динамическое программирование.
Первый подход: Рассмотрим некоторый отрезок из подряд идущих одинаковых букв. Пусть длина отрезка k. Очевидно мы должны изменить хотя бы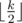 
букв в ней, чтобы не было одинаковых букв подряд. С другой стороны мы можем изменить второй, четвёртый и т.д. символы на букву, которая не равна букве слева и справа от нашего отрезка.
Второй подход: Пусть zka — наименьшее количество изменений, чтобы на префиксе длины k не было двух подряд идущих одинаковых букв и при этом символ s'k был равен букве a. Переберём букву, которую поставим на k + 1-й позиции и если она не равна a сделаем переход. Цена перехода равна 0, если мы поставили ту же букву, что стояла в исходной строке s на k + 1-й позиции. В противном случае цена равна 1.
Сложность: O(n).
665D - Simple Subset
Задачу предложил Zi Song Yeoh zscoder.
Рассмотрим подмножество A, являющееся ответом на задачу. Пусть a, b, c — три произвольных элемента из A и пусть не более чем один из них равен 1. По принципу Дирихле среди этих трёх чисел обязательно найдется пара чисел с одинаковой чётностью. Поскольку в этой паре только одно может быть равно 1, то их сумма чётна и больше 2. Значит подмножество A не является простым. Таким образом, A состоит либо из двух чисел больших единицы (с простой суммой), либо из некоторого количества единиц и возможно одной не единицы (если она равна простому минус один). Первый случай легко обработать за O(n2). Второй случай легко обрабатывается за линейное время. Среди двух ответов, конечно, нужно просто выбрать лучший.
Проверять на простоту числа порядка 2·106 за O(1) можно с помощью обычного или линейного решета Эратосфена.
Сложность: O(n2 + X), где X — максимальное среди заданных чисел.
665E - Beautiful Subarrays
Задачу предложил Zi Song Yeoh zscoder.
Знак 
в разборе обозначает бинарную операцию побитового исключающего или.
Пусть si — xor первых i чисел на префиксе. Тогда полуинтервал (i, j] красивый если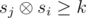 
. Будем перебирать j от 1 до n. Будем рассматривать значения sj как битовые строки. На каждой итерации к ответу нам нужно прибавить величину zj — количество чисел si (i < j) таких, что 
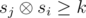. Для этого воспользуемся структурой данных бор. Будем хранить в боре все si для i < j. Кроме самой структуры бора будем в каждой вершине хранить количество листьев в поддереве этой вершины (это легко делать при добавлении новой строки). Для вычисления значения zj будем спускаться по бору, начиная из корня. Будем накапливать число cur равное префиксу ксора числа sj с путём по которому мы спустились по бору. Пусть текущий бит в sj равен b, а i — это глубина вершины в боре в которой мы находимся. Если число cur + 2i ≥ k, то мы сразу можем прибавить к zj количество листьев вершины 
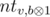, поскольку все эти листья соответствуют si-м гарантированно дающим 
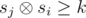. После этого мы должны спуститься в поддерево b. Если же cur + 2i < k, то мы должны просто спуститься в поддерево 
, пересчитав значение cur = cur + 2i.
Сложность по времени и памяти: O(nlogX), где X — наибольший из ксоров на префиксах.
665F - Four Divisors
The editorial for this problem is a little modification of the materials from the lecture of Mikhail Tikhomirov Endagorion of the autumn of 2015 in Moscow Institute of Physics and Technology. Thanks a lot to Endagorion for that materials.
Easy to see that only the numbers of the form p·q and p3 (for different prime p, q) have exactly four positive divisors.
We can easily count the numbers of the form p3 in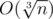 
, where n is the number from the problem statement.
Now let p < q and π(k) be the number of primes from 1 to k. Let's iterate over all the values p. Easy to see that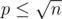 
. So for fixed p we should increase the answer by the value 
.
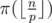So the task is ot to find 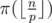~--- the number of primes not exceeding 
, for all p.
Denote pj the j-th prime number. Denote dpn, j the number of k such that 1 ≤ k ≤ n, and all prime divisors of k are at least pj (note that 1 is counted in all dpn, j, since the set of its prime divisors is empty). dpn, j satisfy a simple recurrence:
dpn, 1 = n (since p1 = 2)
dpn, j = dpn, j + 1 + dp⌊ n / pj⌋, j, hence dpn, j + 1 = dpn, j - dp⌊ n / pj⌋, j
Let pk be the smallest prime greater than 
. Then π(n) = dpn, k + k - 1 (by definition, the first summand accounts for all the primes not less than k).
If we evaluate the recurrence dpn, k straightforwardly, all the reachable states will be of the form dp⌊ n / i⌋, j. We can also note that if pj and pk are both greater than , then dpn, j + j = dpn, k + k. Thus, for each ⌊ n / i⌋ it makes sense to keep only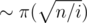 
values of dp⌊ n / i⌋, j.
Instead of evaluating all DP states straightforwardly, we perform a two-step process:
Choose K.
Run recursive evaluation of dpn, k. If we want to compute a state with n < K, memorize the query ``count the numbers not exceeding n with all prime divisors at least k''.
Answer all the queries off-line: compute the sieve for numbers up to K, then sort all numbers by the smallest prime divisor. Now all queries can be answered using RSQ structure. Store all the answers globally.
Run recurisive evaluation of dpn, k yet again. If we want to compute a state with n < K, then we must have preprocessed a query for this state, so take it from the global set of answers.
The performance of this approach relies heavily on Q~--- the number of queries we have to preprocess.
Statement.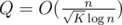 
.
Proof:
Each state we have to preprocess is obtained by following a dp⌊ n / pj⌋, j transition from some greater state. It follows that Q doesn't exceed the total number of states for n > K.
[Q \leq \sum_{j = 1}^{n / K} \pi(\sqrt{n / j}) \sim \sum_{j = 1}^{n / K} \sqrt{n / j} / \log n \sim \frac{1}{\log n}\int_1^{n / K} \sqrt{n / x} dx \sim \frac{n}{\sqrt{K}\log n}]
The preprocessing of Q queries can be done in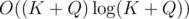 
, and it is the heaviest part of the computation. Choosing optimal 
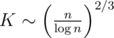, we obtain the complexity 
.
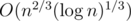Complexity: .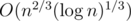
