Всем спасибо за участие! Задачи следуют в порядке, в котором они шли на оригинальном соревновании.
562A - Logistical Questions
(в трансляции: 566C - Logistical Questions)
Формализуем задачу. Нам дано необычное определение расстояния по дереву: ρ(a, b) = dist(a, b)1.5. У каждой вершины есть её вес wi. Нужно как-то так выбрать место x для проведения соревнования, чтобы минимизировать сумму взвешенных расстояний от всех вершин до неё: f(x) = w1ρ(1, x) + w2ρ(x, 2) + ... + wnρ(x, n).
Давайте изучим свойства функции f(x). Мысленно разрешим себе ставить точку x не только в вершины дерева, но и в любую точку на ребре, доопределив естественным образом расстояние от точки внутри ребра до всех остальных вершин (например, середина ребра длины 4 находится на обычном расстоянии 2 от концов ребра).
Утверждение 1. На любом пути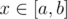 
в дереве функция ρ(i, x) является выпуклой вниз. Действительно, функция dist(i, x) на любом пути выглядит как график функции abs(x), то есть сначала линейно убывает до ближайшей к i точки на пути [a, b], а потом линейно возрастает. Взяв композицию с выпуклой возрастающей функциея t1.5, как нетрудно видеть, мы снова получим выпуклую вниз на пути функцию. Здесь под функцией на пути мы подразумеваем обычную функцию действительной переменной x, где под x мы подразумеваем координату точки x на пути [a, b], или, что то же самое, dist(a, x). Таким образом, каждое из слагаемых в определении функции f(x) выпукло вниз на любом пути в дереве, а значит и функция f(x) выпукла на любом пути в дереве.
Будем называть функции, выпуклые вниз на любом пути в дереве выпуклыми на дереве. Сформулируем пару утверждений про выпуклые функции на дереве.
Утверждение 2. У выпуклой на дереве функции не может быть двух различных локальных минимумов. Действительно, в противном случае на пути между двумя этими минимумами функция сначала возрастает, а в конце убывает, что нарушает условие на выпуклость на этом пути.
Таким образом, у выпуклой вниз функции f(x) есть единственный локальный минимум на дереве, совпадающий с глобальным.
Утверждение 3. Из каждой вершины v дерева существует не более одного ребра, при движении по которому функция убывает. Действительно, в противном случае, если рассмотреть путь, образованный двумя такими рёбрами, то в точке, соответствующей вершине v, функция не будет выпукла вниз.
Назовём направление ребра из вершины v, при движении по которому убывает функция, градиентом функции f в точке x. Согласно утверждению 3, у выпуклой вниз функции f в любой вершине либо однозначно определён градиент, либо вершина является минимумом (глобальным).
Предположим, мы умеем некоторым образом эффективно искать направление градиента из вершины v. Научимся, пользуясь этим знанием и утверждениями 2 и 3 находить глобальный минимум. Если бы наше дерево представляло собой бамбук, то задача бы стала обычной одномерной задачей минимизации выпуклой функции, которая эффективно решается бинарным поиском, т. е. дихотомией. Нам же нужен некоторый эквивалент дихотомии на дереве. Что же это за эквивалент?
Воспользуемся centroid decmoposition! Действительно, возьмём центр дерева (т. е. такую вершину, что размеры всех её поддеревьев не превосходят n / 2). По утверждению 3 можно рассмотреть градиент функции в центре дерева. Во-первых, у функции может не оказаться градиента в центре дерева, что значит, что мы уже нашли оптимум. Иначе, мы знаем, что глобальный минимум расположен именно в поддереве в направлении градиента, значит все остальные поддеревья и сам центр можно выбросить из рассмотрения и оставить только выбранное поддерево. Таким образом, за один подсчёт градиента мы сократили в два раза количество вершин в рассматриваемой части дерева.
Значит, за 
подсчётов градиента мы практически научились решать задачу. Осталось только понять, где именно расположен ответ. Заметим, что глобальный оптимум, скорее всего, окажется внутри какого-то ребра. Тогда, как нетрудно видеть, оптимальной вершиной является один из концов этого ребра, а именно, одна из двух последних рассмотренных в процессе нашего алгоритма вершин. В какой именно можно определить, явно вычислив значение функции в них и взяв меньшее.
Теперь научимся считать направление градиента в вершине v. Зафиксируем одно поддерево ui вершины v. Рассмотрим производную всех слагаемых, соответствующих поддереву ui при движении в поддерево ui, и обозначим её за deri. Тогда, как нетрудно видеть, производная f(x) при движении от x = v в сторону поддерева ui есть - der1 - der2 - ... - deri - 1 + deri - deri + 1 - ... - derk, где k — степень вершины v.
562B - Clique in the Divisibility Graph
(в трансляции: 566F - Clique in the Divisibility Graph)
562C - Restoring Map
(в трансляции: 566E - Restoring Map)
562D - Restructuring Company
(в трансляции: 566D - Restructuring Company)
562E - Max and Min
(в трансляции: 566G - Max and Min)
562F - Matching Names
(в трансляции: 566A - Matching Names)
562G - Replicating Processes
(в трансляции: 566B - Replicating Processes)
