We at GDG IIITA are extremely delighted to have successfully hosted AlgoArena 2025. We want to extend our heartfelt gratitude to each and every one of you for participating in AlgoArena, our flagship coding event. Your enthusiasm, dedication, and creativity have made this event a remarkable success. We hope you enjoyed solving the questions as much as we enjoyed creating them for you. Question statements are attached below for your reference:
A: Squid Game
Idea:rndascode
Can you think of extending the logic for a normal stone paper scissor game to get the solution?
What if we check for a solution by first retracting the left hand and then the right hand? Then each checking becomes same as checking for normal stone paper scissor game.
To solve the problem, follow these steps:
Key Observations
If Ritesh retracts his left hand (
L1), his remaining hand (L2) will compete against Aaryan's hands (L3andL4).If Ritesh retracts his right hand (
L2), his remaining hand (L1) will compete against Aaryan's hands (L3andL4).For each scenario, compare Ritesh's remaining hand with both of Aaryan's hands:
- Ritesh wins if his symbol beats Aaryan's symbol.
- Ritesh loses if Aaryan's symbol beats his.
- The result is a draw if both symbols are the same.
Decision Process
- If Ritesh can avoid losing against both of Aaryan's hands by retracting either hand, output
Left. - If Ritesh can avoid losing by retracting only one specific hand, output
LeftorRight, depending on the safe choice. - If both scenarios result in at least one loss, output
Impossible.
#include <iostream>
#include <string>
using namespace std;
string determineOutcome(char r1, char a1) {
if (r1 == a1) {
return "Draw";
} else if ((r1 == 'R' && a1 == 'S') || (r1 == 'S' && a1 == 'P') || (r1 == 'P' && a1 == 'R')) {
return "Win";
} else {
return "Lose";
}
}
int main() {
int t;
cin >> t;
while (t--) {
string s;
cin >> s;
char rLeft = s[0];
char rRight = s[1];
char aLeft = s[2];
char aRight = s[3];
string outcomeLeft1 = determineOutcome(rRight, aLeft);
string outcomeLeft2 = determineOutcome(rRight, aRight);
string outcomeRight1 = determineOutcome(rLeft, aLeft);
string outcomeRight2 = determineOutcome(rLeft, aRight);
bool leftSafe = (outcomeLeft1 != "Lose" && outcomeLeft2 != "Lose");
bool rightSafe = (outcomeRight1 != "Lose" && outcomeRight2 != "Lose");
if (leftSafe && rightSafe) {
cout << "Left" << endl;
} else if (leftSafe) {
cout << "Left" << endl;
} else if (rightSafe) {
cout << "Right" << endl;
} else {
cout << "Impossible" << endl;
}
}
return 0;
}
B: Binary Step Down
Idea:pranavsingh0111
We need to convert all ones to zeroes .
After each operation, what changes happen to the 1's present in the string? Try writing out a few examples in binary and observe the pattern .
Look carefully at how $$$X$$$ $$$\text&$$$ $$$(-X)$$$ affects different positions .
Can any 1 except the rightmost one be changed by applying one operation?
Only the right-most 1 is converted to 0 after applying one operation. So it is easy to say that the answer to the question is simply the number of 1's in the binary representation .
But why only the right most 1 ??
Let $$$X$$$ be any binary string , for example —
$$$X$$$ = $$$1101.....10000$$$
then $$$(-X)$$$ will be calculated as follows —
Flipping the bits , we get — $$$0010.....01111$$$
Now adding 1 we get — $$$0010.....10000$$$
So $$$X = 1101.....10000$$$ and $$$(-X) = 0010.....10000$$$ , we can now easily see that all the bits on the left side of the right most 1 are opposite in $$$X$$$ and $$$(-X)$$$ , so $$$ X \text& (-X)$$$ will be equal to $$$0000.....10000$$$ and subtracting it will convert the rightmost $$$1$$$ to $$$0$$$ .
#include <bits/stdc++.h>
using namespace std ;
#define int long long
#define endl '\n'
void solve(){
string s ;
cin >> s ;
int n = s.size() ;
int ans = 0 ;
for(int i=0 ; i<n ; i++){
if(s[i]=='1'){
ans++ ;
}
}
cout<<ans<<endl;
}
signed main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t = 1 ;
cin >> t ;
while(t--){
solve();
}
}
C: Lost Element
Idea: pranavsingh0111
Consider inserting a value $$$x$$$ between two numbers $$$a$$$ and $$$b$$$.
Original contribution to score: $$$|a-b|$$$
New contribution after insertion: $$$|a-x| + |x-b|$$$
For score to remain same: $$$|a-b| = |a-x| + |x-b|$$$
This is the triangle inequality!
For each possible position $$$i$$$, we need numbers that work between $$$a[i]$$$ and $$$a[i+1]$$$ This gives us ranges $$$[\min(a_i,a_{i+1}), \max(a_i,a_{i+1})]$$$ for each position.
Now we just need to find the union of all such intervals. But do we actually need to manually calculate the union ? What observation can be made about the union of all such intervals ?
One observation that we can make is that the union of ranges $$$[\min(a_i,a_{i+1}), \max(a_i,a_{i+1})]$$$ and $$$[\min(a_{i+1},a_{i+2}), \max(a_{i+1},a_{i+2})]$$$ is simply $$$[\min(a_i,a_{i+1},a_{i+2}), \max(a_i,a_{i+1},a_{i+2})]$$$
Similary we can say that union of ranges , $$$[\min(a_i,a_{i+1}), \max(a_i,a_{i+1})]$$$ , $$$[\min(a_{i+1},a_{i+2}), \max(a_{i+1},a_{i+2})]$$$ and $$$[\min(a_{i+2},a_{i+3}), \max(a_{i+2},a_{i+3})]$$$ is $$$[\min(a_i,a_{i+1},a_{i+2},a_{i+3}), \max(a_i,a_{i+1},a_{i+2},a_{i+3})]$$$ and so on .
So for the complete union , we get —
Required Interval = $$$[\min(a_i,a_{i+1},...,a_n) , \max(a_i,a_{i+1},...,a_n)]$$$
And Number of elements in this interval = MaxElement — MinElement + 1
#include <bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#define int long long
#define endl '\n'
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds; // *find_by_order, order_of_key
void solve(){
int n ;
cin >> n ;
vector<int> arr(n-1) ;
for(int i=0 ; i<n-1 ; i++){
cin >> arr[i] ;
}
int mx = *max_element(arr.begin(), arr.end()) ;
int mn = *min_element(arr.begin(), arr.end()) ;
cout<<mx+1-mn<<endl;
}
signed main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t = 1 ;
cin >> t ;
while(t--){
solve();
}
}
D: Parity Operations
Idea: rndascode
Can the parity p ever change, irrespective of how we choose $$$a$$$ and $$$b$$$?
When is the initial parity p odd?
Initial Sum Parity:
- The sum of the first $$$n$$$ natural numbers is given by:
- For $$$S$$$ to be odd, $$$n(n+1)$$$ must be divisible by $$$2$$$ but not by $$$4$$$. This happens when $$$n$$$ leaves a remainder of $$$1$$$ or $$$2$$$ when divided by $$$4$$$.
Parity Preservation:
- During each operation, the sum $$$S$$$ changes as:
- This is same as decreasing $$$S$$$ by $$$2 * $$$ min($$$a,b$$$), which will always be even. Thus if $$$S$$$ was initially odd, then odd — even = odd. Thus, the parity of the sum remains unchanged after each operation.
To solve the problem, we need to check if the initial sum $$$S$$$ is odd. This happens if and only if $$$n$$$ leaves a remainder of $$$1$$$ or $$$2$$$ when divided by $$$4$$$. For each test case, we can compute $$$n$$$ mod $$$4$$$ and check if the result is $$$1$$$ or $$$2$$$.
#include <bits/stdc++.h>
using namespace std;
#define int long long
signed main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int t;
cin >> t;
while (t--) {
int n;
cin >> n;
if (n % 4 == 1 || n % 4 == 2)
cout << "YES" << endl;
else
cout << "NO" << endl;
}
return 0;
}
E: Find the Array
Idea: pranavsingh0111
For any index $$$i$$$:
$$$A[i] + B[i]$$$ = ($$$Ans[i]$$$ $$$|$$$ $$$Ans[i+1]$$$) + ($$$Ans[i] \text& Ans[i+1]$$$) = $$$Ans[i] + Ans[i+1]$$$
Since $$$n$$$ is odd , can you find the value of any one element of $$$Ans$$$ ?
Let $$$S = \sum_{i=1}^n A[i] + B[i]$$$
We know that $$$A[i] + B[i]$$$ = $$$Ans[i] + Ans[i+1]$$$
So $$$S = (Ans[1] + Ans[2]) + (Ans[2] + Ans[3]) + ...... + (Ans[n] + Ans[1]) $$$
or $$$S = 2 \sum_{i=1}^n Ans[i]$$$ (each element appears twice in sum)
or $$$SUM$$$ = $$$S/2$$$
Now we need to find the value of any one element of $$$Ans$$$ , we then know the value of $$$(Ans[i] + Ans[i+1])$$$ , so if we get any one value , we can the value of $$$Ans[i+1]$$$ easily .
Let $$$X = (A[2] + B[2]) + (A[4] + B[4]) + ..... + (A[n-1] + B[n-1])$$$
Note that since n is odd , n-1 will always lie in this series as it will be even .
So $$$X = Ans[2] + Ans[3] + Ans[4] + Ans[5] + ..... + Ans[n-1] + Ans[n] $$$
Now , Using the value of $$$SUM$$$ and $$$X$$$ , we get $$$Ans[1] = SUM - X$$$
Now we can get the rest of the elements by simple substitution .
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
void solve(){
int n ;
cin >> n ;
vector<int> A(n) , B(n) , Ans(n,-1) ;
for(int i=0 ; i<n ; i++){
cin >> A[i] ;
}
for(int i=0 ; i<n ; i++){
cin >> B[i] ;
}
int totalSum = 0 ;
for(int i=0 ; i<n ; i++){
totalSum += (A[i] + B[i]) ;
}
totalSum /= 2 ;
// x stores ans1 + 2*ans2 + ans3
int x = (A[0] + B[0]) + (A[1] + B[1]) ;
//adding ans4 + ans5 + ans6 ... + ansn
for(int i=3 ; i<n ; i+=2){
x += (A[i] + B[i]) ;
}
// now x contains ans1 + 2*ans2 + ans3 + ans4 + ans5 + ans6 ... + ansn
Ans[1] = x - totalSum ;
Ans[0] = (A[0] + B[0] - Ans[1]) ;
for(int i=1 ; i<n-1 ; i++){
int sum = A[i] + B[i] ;
Ans[i+1] = sum - Ans[i] ;
}
for(int i=0 ; i<n ; i++){
int first = i , second = (i+1) % n ;
int check1 = (Ans[first]|Ans[second]) ;
int check2 = (Ans[first]&Ans[second]) ;
if(check1!=A[i] || check2!=B[i]){
cout<<-1<<endl;
return ;
}
}
for(int i=0 ; i<n ; i++){
cout<<Ans[i]<<" ";
}cout<<endl;
}
signed main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t = 1 ;
cin >> t ;
while(t--){
solve();
}
}
F: CodeLand Ratings
Idea: schrodeR
Can you store values and index together?
Sort the vector and think of a binary search solution.
Think of making a prefix minimum and suffix maximum array.
Initially we have been given an array $$$a$$$ and we have to tell if there exists a pair of indices $$$i$$$, $$$j$$$ such that $$$a[i] \leq x \leq a[j]$$$ for each query. Obviously, brute force won't work as iterating over all pairs would be $$$O(n^2)$$$ and for total complexity will be $$$O(q*n^2)$$$ but we would have to optimise it to $$$O(log(n))$$$ query time using binary search for each query.
To solve this problem, first create a vector of pairs $$$v$$$ storing $$${value, index}$$$ pairs. We are doing so to keep a track of what was the original index for each value in array a. Sort this vector.
Construct two auxiliary arrays: $$$pref$$$ and $$$suff.$$$
At index $$$idx$$$ of vector $$$v$$$ let $$$k=v[idx].first$$$ then $$$pref[idx]$$$ stores the minimum value of $$$v[i].second$$$ for all $$$1 \leq i \leq idx$$$. Hence, $$$pref[idx]$$$ will store the minimum index from the original array $$$a$$$ whose value is $$$\leq k .$$$
Similarly, at index $$$idx$$$ of vector $$$v$$$ let $$$k=v[idx].first$$$ then $$$suff [idx]$$$ stores the maximum value of $$$v[i].second$$$ for all $$$idx \leq i \leq n$$$. Hence, $$$suff[idx]$$$ will store the maximum index from the original array $$$a$$$ whose value is $$$\geq k .$$$
Create a vector $$$v_1$$$ containing all values of array $$$a$$$ in ascending order for easier implementation.
For a query for value $$$x$$$: use binary search on $$$v_1$$$ to find:
$$$i_1 $$$= index of $$$v1$$$ such that $$$v1[i_1]$$$ is just smaller than equal to x.
$$$i_2 $$$= index of $$$v1$$$ such that $$$v1[i_2]$$$ is just greater than equal to x.
$$$pref[i_1]$$$ gives minimum index $$$i$$$ from original array where $$$a[i] \leq x$$$
$$$suff[i_2]$$$ gives maximum index $$$j$$$ from original array where $$$a[j] \geq x$$$
Check if $$$pref[i_1] < suff[i_2]$$$: Output "YES" otherwise Output "NO".
#include<bits/stdc++.h>
using namespace std;
#define int long long
signed main()
{
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int n;cin>>n;
//using 1-based indexing for all vectors.
vector<int> a(n+1,0);
for(int i=1;i<=n;i++){
cin>>a[i];
}
int q;cin>>q;
vector<pair<int,int>>v(n+1);
vector<int> v1(n+1,0);
for(int i=1;i<=n;i++){
v[i]=make_pair(a[i],i);
v1[i]=a[i];
}
sort(v.begin(),v.end());
sort(v1.begin(),v1.end());
vector<int> pref(n+2,1e9),suff(n+2,0);
for(int i=1;i<=n;i++){
pref[i]=min(pref[i-1],v[i].second);
}
for(int i=n;i>=1;i--){
suff[i]=max(suff[i+1],v[i].second);
}
while(q--){
int x;cin>>x;
auto it=lower_bound(v1.begin(),v1.end(),x);
if(it==v1.end()){
cout<<"NO\n";
continue;
}
auto it1=upper_bound(v1.begin(),v1.end(),x);
if(it1==v1.begin()){
cout<<"NO\n";
continue;
}
it1--;
int i2=it-v1.begin();
int i1=it1-v1.begin();
if(pref[i1] < suff[i2]){
cout<<"YES\n";
}
else{
cout<<"NO\n";
}
}
return 0;
}
G: AStack Data Structure
Idea: pranavsingh0111
Before approaching this problem, one should be familiar with:
How to calculate minimum moves for standard Tower of Hanoi
Basic Modular Arithmetic ( just multiplication )
Think about the problem in reverse . Instead of moving from B and C to A ,consider starting with sorted stack in A and then dividing into odd and even stacks .
Number of moves will remain same . This gives clearer picture of required operations
Try to put the three largest blocks into their respective stacks using minimum moves (this can be done by using knowledge about the standard Tower of Hanoi )
Can you observe the recursive nature of the problem ??
We are going to look at the solution with the help of an example for n = 7 for better understanding of the recursion.
Originally all the 7 elements are present in stackA 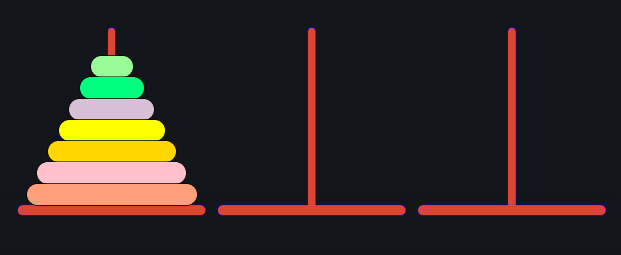
Now firstly, we will move the 7th block to any one of the empty stacks, in this case, we are moving it to stackC. To do so, we will have to move the top 6 elements to StackB. We know this will take $$$2^6 - 1$$$ moves (Classical Tower Of Hanoi problem). We will then use 1 move to move the last element to StackC.
So the total number of moves till now are $$$2^6$$$ and the configuration looks something like this: 
Now we can easily see that the second biggest element (6 in this case) is already at the required position. So there is no point in moving that element. We now have to shift our focus to the third biggest element (5 in this case).
The correct position for element 5 is above 7. So again we have to move the top 4 elements to StackA. This will take $$$2^4 - 1$$$ moves.
The total number of moves used till now will be $$$2^6 + 2^4 - 1$$$ and the configuration will look something like this: 
We will now simply move the $$$5^{th}$$$ element to its place in StackC using $$$1$$$ move.
The total moves used will be $$$2^6 + 2^4 - 1 + 1 = 2^6 + 2^4$$$ and we will reach this position: 
Now you can see that we have reached a situation similar to the one we were originally at. We have a stack in StackA, and we have to divide it into StackB and StackC but the $$$n$$$ is now $$$(n-3)$$$.
So we get this recursive formula:
Moves for $$$n = 2^{n-1} + 2^{n-3} + \text{Moves for } (n-3)$$$
NOTE:
While computing the answer, we will store the answer for all $$$n$$$ from $$$1$$$ to $$$10^6$$$ in the beginning and not compute it for each testcase separately. This will save time.
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define MOD 1000000007
vector<int> ans(1000001) ;
int exp(int x, int n) {
x %= MOD;
int res = 1;
while (n > 0) {
if (n % 2 == 1) { res = res * x % MOD; }
x = x * x % MOD;
n /= 2;
}
return res;
}
void precompute(){
ans[0] = 0 ;
ans[1] = 1 ;
ans[2] = 2 ;
for(int i=3 ; i<1000001 ; i++){
int temp1 = exp(2,i-1) ;
int temp2 = exp(2,i-3) ;
int temp3 = ans[i-3] ;
ans[i] = (temp1 + temp2 + temp3) % MOD ;
}
}
void solve(){
int n ;
cin >> n ;
cout<<ans[n]<<endl;
}
signed main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t = 1 ;
cin >> t ;
precompute() ;
while(t--){
solve();
}
}
H: Array Divisibility
Idea: rndascode
Count of elements from $$$a+1$$$ to $$$b$$$ divisible by $$$k$$$
= Count of elements from $$$1$$$ to $$$b$$$ divisible by $$$k$$$ — Count of elements from $$$1$$$ to $$$a$$$ divisible by $$$k$$$
= $$$\lfloor b/k \rfloor - \lfloor a/k \rfloor$$$.
Does Modular Division work like arithmetic division, even when $$$a$$$ is not exactly divisible by $$$k$$$? No, it doesn't.
Let us consider the problem simply without the constraints first. Let us assume $$$a$$$ and $$$b$$$ are both give in integer form.
Count of elements from $$$a+1$$$ to $$$b$$$ divisible by $$$k$$$
= Count of elements from $$$1$$$ to $$$b$$$ divisible by $$$k$$$ — Count of elements from $$$1$$$ to $$$a$$$ divisible by $$$k$$$
= $$$\lfloor b/k \rfloor - \lfloor a/k \rfloor$$$.
Our entire solution focusses on implementing this formula for very large numbers.
As the numbers are very big, it is not possible to directly implement this formula. We need the answer mod $$$6991$$$. Using modular arithmetic the equation can be changed to
$$$((b\pmod{6991}*k^{-1}) - (a\pmod{6991}*k^{-1}) + (6991)) \mod{6991}$$$ where $$$k^{-1}$$$ is the modular multiplicative inverse of $$$k$$$ wrt $$$6991$$$.
To efficiently compute $$$b\pmod{6991}$$$ and $$$a\pmod{6991}$$$ we will use the following way:
Start with number $$$0$$$.
For every new digit, compute number = number * base + digit.
Take remainder at each step.
This gives us our required modulus result irrespective of the base of the number.
Our implementation has a problem however. Modular division does not work like arithmetic division. Eg: $$$(44/2)$$$ mod $$$6991$$$ = $$$22$$$, but $$$(45/2)$$$ mod $$$6991$$$ = $$$3518$$$. We need to ensure floor at both computations.
Thus our modified equation becomes:
$$$((b - (b \mod k))/k) - ((a - (a \mod k))/k)$$$ .
Using modular arithmetic the required answer is:
$$$T1 = ((b\pmod{6991}-b\pmod{k}+6991) * k^{-1}) \mod{6991}$$$
$$$T2 = ((a\pmod{6991}-a\pmod{k}+6991) * k^{-1}) \mod{6991}$$$
$$$Ans = (T1 - T2 + 6991) \mod 6991$$$
#include<bits/stdc++.h>
using namespace std;
#define int long
const int MOD = 6991;
long long exp(long long x, long long n, long long m) {
x %= m;
long long res = 1;
while (n > 0) {
if (n % 2 == 1) { res = res * x % m; }
x = x * x % m;
n /= 2;}
return res;}
long long fun(string &a, int m, int base){
int res=0;
for(int i=0;i<a.size();i++){
res = (res*base + int(a[i]-'0'))%m;}
return res%m;}
signed main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int t;
cin>>t;
while(t--){
int a1,b1,k;
cin>>a1>>b1>>k;
string a,b;
cin>>a>>b;
int k_inv = exp(k, MOD-2, MOD);
int term1 = (((fun(a,MOD,2) - fun(a,k,2) + MOD)%MOD) * (k_inv%MOD))%MOD;
int term2 = (((fun(b,MOD,10) - fun(b,k,10) + MOD)%MOD) * (k_inv%MOD))%MOD;
int res = (term2 - term1 + MOD)%MOD;
cout<<res<<endl;}
return 0;}
I: Tournament Ratings
Idea: schrodeR
Try using ordered set with difference array approach.
For every element $$$a_i$$$ try to find the number of elements bigger than it on the right side of the array and the number of elements smaller than it on the left side of the array.
#include<bits/stdc++.h>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
using namespace std;
using namespace __gnu_pbds;
typedef tree<pair<int,int>, null_type, less<pair<int,int>>, rb_tree_tag, tree_order_statistics_node_update> pbds; // find_by_order, order_of_key
#define endl "\n"
#define int long long
int32_t main()
{
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int n;cin>>n;
vector<int> a(n+1,0);
for(int i=1;i<=n;i++){
cin>>a[i];
}
int q;cin>>q;
map<int,int> diff;
pbds start,end;
for(int i=1;i<=n;i++){
int now=start.order_of_key(make_pair(a[i],i));
diff[a[i]+1]-=now;
start.insert(make_pair(a[i],i));
}
for(int i=n;i>=1;i--){
int now=end.order_of_key(make_pair(a[i],i));
int val=((int)end.size())-now;
diff[a[i]]+=val;
end.insert(make_pair(a[i],i));
}
auto it=diff.begin();
it++;
auto it1=diff.begin();
for(;it!=diff.end();it++){
it->second+=it1->second;
it1=it;
}
while(q--){
int x;cin>>x;
auto it2=diff.upper_bound(x);
if(it2==diff.begin()){
cout<<0<<endl;
continue;
}
else{
it2--;
cout<<(it2->second)<<endl;
}
}
return 0;
}
J: BST Errors
Idea: rndascode
Can we use a DFS based approach to count the number of violations?
Can we use Small to Large Merging to optimize our solution?
To solve this problem efficiently, we can leverage appropriate data structures to store the Binary Tree and perform operations on it. Here's a step-by-step approach:
DFS for Counting Violations: We can use Depth-First Search (DFS) to count the number of nodes that violate the BST properties in each subtree. To check each node's validity in the BST, we compare its value with the maximum and minimum permissible values for that node as we move from the root down to the leaves.
Complexity Analysis: This approach allows us to check the entire tree in $$$O(N)$$$ time, where $$$N$$$ is the number of nodes, because each node is visited only once. At each node, we compare its value with the maximum and minimum bounds passed from its parent, updating these bounds as we recurse deeper.
Tracking Violating Nodes in Order: We can use sets to keep track of nodes that violate the BST property, storing them in ascending order by node number. To efficiently merge these sets as we move up the tree, we can use a technique called small to large merging.
Small to Large Merging Strategy: Starting from the leaf nodes and moving up toward the root in DFS, we store query nodes in the required order (ascending by node number within each query). For each query, the required nodes are stored, allowing us to merge the child node sets with their respective parent sets efficiently.
This approach provides an efficient solution that respects the problem's constraints, ensuring that the operations required per query are minimized through effective data structure usage and ordered processing.
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e5 + 5;
vector<pair<int, char>> tree[MAXN];
int node_values[MAXN];
int violations_count[MAXN];
set<int> violations_set[MAXN];
set<int> query_nodes;
int level[MAXN];
vector<int> queries[MAXN];
vector<int> query_nodes_vec;
vector<int> result[MAXN];
bool is_violated[MAXN];
map<int, set<int>> violations;
void dfs(int node, int parent, int min_val, int max_val, int lvl) {
level[node] = lvl;
if (!(min_val < node_values[node] && node_values[node] < max_val)) {
is_violated[node] = true;
violations_set[node].insert(node);
violations_count[node] = 1;
} else {
violations_count[node] = 0;
}
for (auto &[child, direction] : tree[node]) {
if (child == parent) continue;
if (direction == 'l') {
dfs(child, node, min_val, min(max_val, node_values[node]), lvl + 1);
} else {
dfs(child, node, max(min_val, node_values[node]), max_val, lvl + 1);
}
if (violations_set[child].size() > violations_set[node].size()) {
swap(violations_set[node], violations_set[child]);
}
violations_set[node].insert(violations_set[child].begin(), violations_set[child].end());
violations_count[node] += violations_count[child];
}
if (query_nodes.find(node) != query_nodes.end()) {
violations[node] = violations_set[node];
}
}
int main() {
int N;
cin >> N;
for (int i = 0; i < N; i++) {
cin >> node_values[i];
}
for (int i = 0; i < N - 1; i++) {
int u, v;
char dir;
cin >> u >> v >> dir;
u--; v--;
tree[u].emplace_back(v, dir);
tree[v].emplace_back(u, dir);
}
int Q;
cin>>Q;
for (int i = 0; i < Q; i++) {
int x; cin>>x; x--;
query_nodes.insert(x);
query_nodes_vec.push_back(x);
}
dfs(0, -1, INT_MIN, INT_MAX, 0);
for(auto node:query_nodes_vec){
cout<<node+1<<" ";
if (violations[node].empty()) {
cout << -1;
} else {
for (int v : violations[node]) {
cout << v + 1 << " ";
}
}
cout<<endl;
}
for (int i = 0; i < N; i++) {
cout << violations_count[i]<< " ";
}
cout << endl;
return 0;
}





