↵
The motivation↵
------------------↵
There are many examples in CP where we need to maximise or minimise the value of some function $f$. If the function is unimodal, there is no problem using ternary search. But if it's not, there's nothing to do. Of course, if $f$ is random, we should check all its values. Fortunately, intuition tells us that if the function is close to unimodal, we can also use ternary search on a large part of its area of definition
↵
Мотивация↵
------------------↵
В олпроге есть много примеров, когда нам нужно максимизировать или минимизировать значение некоторой функции $f$. Если функция унимодальна, то нет проблем с использованием тернарного поиска. Но если это неправда, то делать нечего. Конечно, если $f$ случайна, нужно проверить все ее значения. К счастью, интуиция подсказывает нам, что если функция близка к унимодальной, то мы можем использовать тернарный поиск и на большей части ее области определения.↵
↵
↵
###
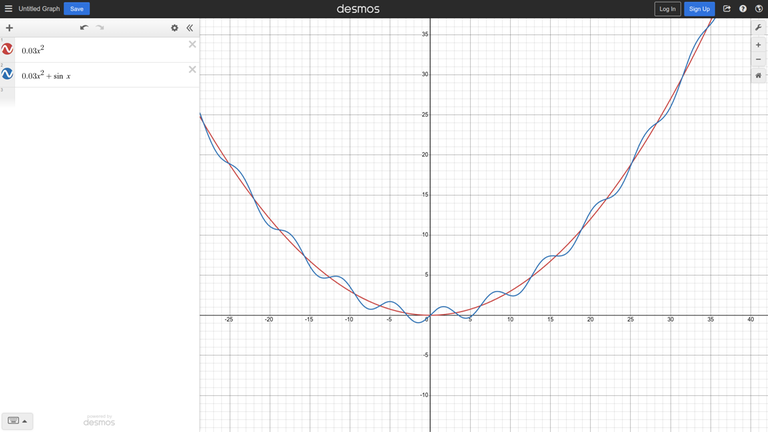
Consider the unimodal function $0.03x^2$ after adding some noise
Рассмотрим унимодальную функцию $0.03x^2$, добавив к ней немного шума ($sin (x)$)
↵
<spoiler summary="Graph">↵
↵
</spoiler>↵
↵
↵
In this example, we can put it more formally — the derivative of the function is
↵
В данном примере мы можем показать это более формально: производная функции равна $0.06x + cos(x)$,
#### The first optimisation↵
So, the first idea is to run the ternary search using not
↵
#### Первая оптимизация↵
Итак, первая идея — запустить тернарный поиск, используя не `while (r - l > eps)`
#### The second optimisation↵
It is mentioned in [this blog](https://codeforces.me/blog/entry/60702). It tells us a similar idea of splitting all argument values into blocks and applying ternary search on them.↵
↵
This is the only thing related to the blog that I found. I tried googling and asking people involved in CP, but none of them knew about it before.↵
↵
### Testing↵
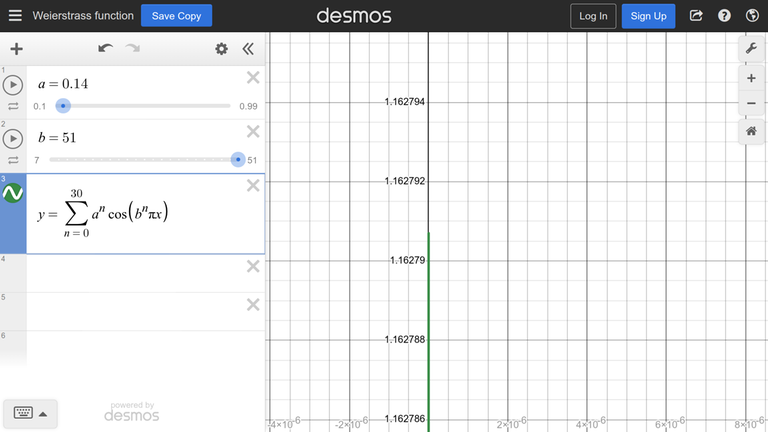
The function from the example is boring, so consider a more interesting function: [Weierstrass function
↵
#### Вторая оптимизация↵
Она упоминается в [этом блоге] (https://codeforces.me/blog/entry/60702). В нем рассказывается аналогичная идея разбиения всех значений аргументов на блоки и применения к ним троичного поиска.↵
↵
Это единственная связанная с блогом идея, которую я нашел в Интернете. Я пробовал гуглить и спрашивать людей, занимающихся олпрогой, но никто из них не знал об этом раньше.↵
↵
### Тесты↵
Функция из примера скучна, поэтому рассмотрим более интересную: [функция Вейерштрасса](https://www.desmos.com/calculator/lae5b4wdhq).↵
↵
↵
<spoiler summary="Spoiler">↵
↵
</spoiler>↵
↵
↵
<spoiler summary="Code">↵
↵
~~~~~↵
#include <bits/stdc++.h>↵
#define M_PI 3.14159265358979323846↵
using namespace std;↵
#define ld long double↵
ld Weierstrass(ld x) {↵
ld y = 0;↵
for (int i = 0; i < 30; i++) y += pow(0.14, i) * cos(pow(51, i) * M_PI * x);↵
return y;↵
}↵
ld Classical_ternary(ld f(ld), ld l = -1, ld r = 1, ld eps = 1e-7) {↵
while (r - l > eps) {↵
ld midl = l + (r - l) / 3;↵
ld midr = r - (r - l) / 3;↵
if (f(midl) > f(midr)) r = midr;↵
else l = midl;↵
}↵
return f(l);↵
}↵
int main() {↵
cout << Classical_ternary(Weierstrass) << endl;↵
}↵
~~~~~↵
↵
</spoiler>↵
↵
↵
Let's split the arguments into blocks. Since the arguments are real, we will not actually split them explicitly into blocks, we will take the maximum in some range near the argument
↵
Давайте разделим аргументы на блоки. Поскольку аргументы вещественные, мы не будем явно разбивать их, а возьмем максимум в некотором диапазоне вблизи аргумента.↵
↵
<spoiler summary="Blocks">↵
↵
~~~~~↵
ld Blocks(ld f(ld), ld l = -1, ld r = 1, ld eps = 1e-7) {↵
int iter = 10000;↵
while (r - l > eps) {↵
ld midl = l + (r - l) / 3;↵
ld midr = r - (r - l) / 3;↵
ld vall = -2e9, valr = -2e9;↵
for (ld x = midl, i = 0; i < iter; x += eps, i++) vall = max(vall, f(x));↵
for (ld x = midr, i = 0; i < iter; x += eps, i++) valr = max(valr, f(x));↵
if (vall > valr) r = midr;↵
else l = midl;↵
}↵
return f(l);↵
}↵
~~~~~↵
</spoiler>↵
↵
↵
<spoiler summary="Take maximum">↵
~~~~~↵
ld Blocks(ld f(ld), ld l = -1, ld r = 1, ld eps = 1e-7) {↵
int iter = 10000;↵
ld ans = -2e9;↵
while (r - l > eps) {↵
ld midl = l + (r - l) / 3;↵
ld midr = r - (r - l) / 3;↵
ld vall = -2e9, valr = -2e9;↵
for (ld x = midl, i = 0; i < iter; x += eps, i++) vall = max(vall, f(x));↵
for (ld x = midr, i = 0; i < iter; x += eps, i++) valr = max(valr, f(x));↵
ans = max({ans, vall, valr});↵
if (vall > valr) r = midr;↵
else l = midl;↵
}↵
return max(ans, f(l));↵
}↵
~~~~~↵
</spoiler>↵
↵
↵
##The third optimisation↵
Let's change the constant $3$ in the code. We will call it $C$. It is not new to experienced people, often it is good to choose $C$ equal to $2$ (binary search by the derivative) or $\frac{\sqrt5+1}{2}$ (golden ratio).↵
As we are cutting out $\frac{1}{C}$ part of our interval on each iteration, the probability of the maximum being indise the cut-off part decreases as C increases.↵
↵
Let's choose $C = 100$ and run ternary search. As we already know, taking maximum of all function calls is very good optimisation, so I have already added it.↵
↵
<spoiler summary="Code">↵
~~~~~↵
ld find_maximum(ld f(ld), int C = 3, ld l = -1, ld r = 1, ld eps = 1e-7) {↵
ld ans = -2e9;↵
while (r - l > eps) {↵
ld midl = l + (r - l) / C;↵
ld midr = r - (r - l) / C;↵
ld vall = f(midl), valr = f(midr);↵
ans = max({ans, vall, valr});↵
if (vall > valr) r = midr;↵
else l = midl;↵
}↵
return max(ans, f(l));↵
}↵
~~~~~↵
</spoiler>↵
↵
If we run it with $C = 3$, we get $1.13140$ (the algo is the same as the classic ternary search, but we take the maximum, so the answer is much better).↵
Now let's now increase $C$ and watch the answer increases:↵
↵
We run it with $C = 30$ and get $1.16275$.↵
We run it with $C = 100$ and get ... $1.15444$↵
↵
In fact, increasing $C$ does not guarantee a better answer.↵
### The fourth optimisation↵
Let's bruteforce all values of $C$ from 3 to 100 and take the best answer:↵
↵
`for (int C = 3; C < 100; C++) res = max(res, find_maximum(Weierstrass, C));`↵
↵
It gives us $1.16279$ and works faster than block splitting. To compare them further, we need to change the function, because both methods return values that are very close to the answer.↵
↵
Let's use $a = 0.88$ and $b = 51$ for the Weierstrass function. Note that it is impossible to see the actual maximum of the function in Desmos.↵
↵
I will compare the above 2 approaches on Codeforces Custom test.↵
↵
<spoiler summary="C < 100">↵
↵
~~~~~↵
Blocks res: 6.6809↵
Blocks time: 3.645↵
100-ternary res: 6.27581↵
100-ternary time: 0.753↵
~~~~~↵
</spoiler>↵
↵
↵
<spoiler summary="C < 200">↵
↵
~~~~~↵
Blocks res: 6.6809↵
Blocks time: 3.365↵
200-ternary res: 6.48924↵
200-ternary time: 2.725↵
~~~~~↵
↵
↵
</spoiler>↵
↵
↵
<spoiler summary="C < 400">↵
↵
~~~~~↵
Blocks res: 6.6809↵
Blocks time: 3.442↵
400-ternary res: 7.05544↵
400-ternary time: 10.751↵
~~~~~↵
</spoiler>↵
↵
I tried combining these methods together, but is performs worse than both techniques (because I used $1000$ iterations instead of $10000$ and bruteforced $C < 10$ not to run out of time).↵
↵
Conclusion↵
------------------↵
On the function I considered, both approaches are good enough. On real contests I only used my approach.↵
↵
From recent problems, [problem:2035E], I have used this technique successfully. Here is the implementation for integer arguments: [submission:288346163].↵
↵
If you know how to find the maximum better (not by simulated annealing), please write.
↵
##Третья оптимизация↵
Давайте изменим константу $3$ в коде. Назовем ее $C$. Опытным олпрогерам известно, что часто хорошо выбрать $C$ равной $2$ (бинарный поиск по производной) или $\frac{\sqrt5+1}{2}$ (терпоиск с золотым сечением).↵
Поскольку на каждой итерации мы отбрасываем $\frac{1}{C}$ часть нашего интервала, вероятность того, что максимум окажется внутри отрезанной части, уменьшается с увеличением C.↵
↵
Выберем $C = 100$ и запустим тернарный поиск. Как мы уже знаем, взятие максимума из всех вызовов функций — очень хорошая оптимизация, поэтому я сразу ее добавлю.↵
↵
↵
<spoiler summary="Code">↵
~~~~~↵
ld find_maximum(ld f(ld), int C = 3, ld l = -1, ld r = 1, ld eps = 1e-7) {↵
ld ans = -2e9;↵
while (r - l > eps) {↵
ld midl = l + (r - l) / C;↵
ld midr = r - (r - l) / C;↵
ld vall = f(midl), valr = f(midr);↵
ans = max({ans, vall, valr});↵
if (vall > valr) r = midr;↵
else l = midl;↵
}↵
return max(ans, f(l));↵
}↵
~~~~~↵
</spoiler>↵
↵
Если мы запустим его при $C = 3$, то получим $1,13140$ (алгоритм тот же, что и в классическом троичном поиске, но мы берем максимум, поэтому ответ намного лучше).↵
Теперь давайте увеличим $C$ и посмотрим, как увеличится ответ:↵
↵
Мы запускаем его с $C = 30$ и получаем $1,16275$.↵
Запускаем его с $C = 100$ и получаем... $1,15444$.↵
↵
Дело в том, что увеличение $C$ не гарантирует увеличения ответа.↵
↵
### Четвертая оптимизация↵
Давайте переберем все значения $C$ от 3 до 100 и возьмем лучший ответ:↵
↵
`for (int C = 3; C < 100; C++) res = max(res, find_maximum(Weierstrass, C));`↵
↵
Это дает нам $1,16279$ и работает быстрее, чем разбиение на блоки. Чтобы сравнивать эти подходы дальше, нам нужно изменить функцию, потому что оба метода возвращают значения, которые очень близки к ответу.↵
↵
Используем $a = 0,88$ и $b = 51$ для функции Вейерштрасса. Обратите внимание, что в Desmos невозможно увидеть фактический максимум функции.↵
↵
Я сравню эти два подхода в Запуске Codeforces.↵
↵
<spoiler summary="C < 100">↵
↵
~~~~~↵
Blocks res: 6.6809↵
Blocks time: 3.645↵
100-ternary res: 6.27581↵
100-ternary time: 0.753↵
~~~~~↵
</spoiler>↵
↵
↵
<spoiler summary="C < 200">↵
↵
~~~~~↵
Blocks res: 6.6809↵
Blocks time: 3.365↵
200-ternary res: 6.48924↵
200-ternary time: 2.725↵
~~~~~↵
↵
↵
</spoiler>↵
↵
↵
<spoiler summary="C < 400">↵
↵
~~~~~↵
Blocks res: 6.6809↵
Blocks time: 3.442↵
400-ternary res: 7.05544↵
400-ternary time: 10.751↵
~~~~~↵
</spoiler>↵
↵
Я попробовал объединить эти методы вместе, но результат оказался хуже, чем у обоих методов (потому что я использовал $1000$ итераций вместо $10000$ и перебор $C < 10$, чтобы влезть в ТЛ).↵
↵
Вывод↵
------------------↵
На рассмотренной мной функции оба подхода достаточно хороши. На реальных соревнованиях я использовал только свой подход (четвертую оптимизацию).↵
↵
Из недавних задач, [problem:2035E], я успешно использовал эту технику. Вот реализация для целочисленных аргументов: [submission:288346163].↵
↵
Если вы знаете, как найти максимум лучше (не методом имитации отжига), пожалуйста, напишите.↵
↵
↵






