**Part1: Introduction**↵
↵
[Atcoder Beginner Contest 279](https://atcoder.jp/contests/abc279) is good for learning [generating functions (GFs)](https://en.wikipedia.org/wiki/Generating_function). The English version tutorial of [279Ex](https://atcoder.jp/contests/abc279/tasks/abc279_h) has already been posted on the [MathStackExchange](https://math.stackexchange.com/questions/4586327/sum-of-product-of-min-which-is-related-to-the-pentagonal-number-theorem) by a kind person. Unfortunately, the English tutorial on [279G](https://atcoder.jp/contests/abc279/tasks/abc279_g) is not available. Now I would like to make a second-hand tutorial on [279G](https://atcoder.jp/contests/abc279/tasks/abc279_g) based on [PCTprobability's idea](https://atcoder.jp/contests/abc279/editorial/5293). I spend a huge amount of time understanding this idea. For contestants at about my level, it is quite difficult to understand ↵
[the idea](https://atcoder.jp/contests/abc279/editorial/5293) even if it is written in English, let alone it is written in Japanese only (My Japanese is N5 level). I will make the following contributions. ↵
↵
(1)Write the tutorial in English. The original tutorial is in Japanese only. ↵
↵
(2)Fill in the details. I believe you can understand my words.↵
↵
(3)Offer an accepted implementation.↵
↵
I have to state that, using generating function is definitely not the best way to solve this problem. It could be solved much simpler by using dynamic programming with [monotone deque optimization](https://robert1003.github.io/2020/02/16/dp-opt-monotone-queue.html). However, this problem is also a good chance to learn [generating functions (GFs)](https://en.wikipedia.org/wiki/Generating_function). Generating functions encode the information of sequences in a continuous way. If you do not know anything about GFs, I suggest you read:↵
↵
(1) How to use GFs to solve recurrence? [Link](https://math.stackexchange.com/questions/1544784/generating-functions-recurrence-relations).↵
↵
(2) How to prove the Vandemonde convolution identity using GFs? [Link](https://math.stackexchange.com/questions/3494228/proof-vandermondes-identity-using-generating-function).↵
↵
(3) And most relevant to this problem, how to solve partitions using GFs? [Link](https://en.wikipedia.org/wiki/Pentagonal_number_theorem).↵
↵
The most important notation $\[x^k\]f(x)$ denotes the coefficient of $x^k$ in function $f(x)$. For example, $\[x^2\](x^3+2x^2+1)=2$. And $\[x^2\]\frac{1}{1-2x}=4$, because we can expand $\frac{1}{1-2x}$ to $\sum\limits_{i=0}^\infty (2x)^i$ in the region of convergence $(-\frac{1}{2}, \frac{1}{2})$. So the coefficient of $x^2$ is $4$. ↵
↵
**Part2: Problem Statement**↵
↵
[The problem](https://atcoder.jp/contests/abc279/tasks/abc279_g) says: ↵
There is a grid with $1×N$ squares, numbered $1,2,…,N$ from left to right.↵
↵
Takahashi prepared paints of $C$ colors and painted each square in one of the C colors.↵
Then, there were at most two colors in any consecutive K squares.↵
Formally, for every integer $i$ such that $1≤i≤N−K+1$, there were at most two colors in squares $i,i+1,…,i+K−1$.↵
↵
In how many ways could Takahashi paint the squares?↵
Since this number can be enormous, find it modulo $998244353$.↵
↵
$\cdot \text{All inputs are integers.}$↵
↵
$\cdot 2 \leq K \leq N \leq 10^6$.↵
↵
$\cdot 1 \leq C \leq 10^9$.↵
↵
Test Case $1$: $N=K=C=3$. In this input, we have a $1×3$ grid. Among the $27$ ways to paint the squares, there are $6$ ways to paint all squares in different colors, and the remaining $21$ ways are such that there are at most two colors in any consecutive three squares.↵
↵
Test Case $2$: $N=10, K=5, C=2$: Print $1024$.↵
↵
Test Case $3$: $N=998, K=244, C=353$: Print $952364159$.↵
↵
**Part3: Idea**↵
↵
(1) What are GFs good at? Gf is good at solving partitions, for example, the [Pentagonal number theorem](https://en.wikipedia.org/wiki/Pentagonal_number_theorem). So, the first step is to compress the colors by [Run-Length Encoding (RLE)](https://en.wikipedia.org/wiki/Run-length_encoding). For example, if the colors are $(1,1,1,2,2,3,2,2)$, then they are uniquely compressed to $((1, 3), (2, 2), (3, 1), (2, 2))$. With RLE, $[1, n]$ is **partitioned** into $l$ segments with different colors. Let me denote these segments as $S_1, S_2, ..., S_l$. Please note that adjacent segments must be painted with different colors, otherwise you can merge the adjacent segments into one, which violates the definition of RLE. The idea to divide the interval into segments for counting also appears in Pinely Round Problem D.↵
↵
(2)Consider $2 \leq i \leq l-1$. If $|S_i| \leq K-2$, then $S_{i+1}$ only has one choice: Paint it with the same color as $S_{i-1}$. Otherwise, the last element of $S_{i-1}$, the whole segment $S_{i}$ and the first element of $S_{i+1}$ will form an interval with size $\leq K$ and three colors, violating the rule. If $|S_i| > K-2$, then $S_{i+1}$ has $C-1$ choices. It is only required that the color of $S_{i+1}$ is different from that of $S_{i}$.↵
↵
(3)I claim that the generating function for segmentation of length $l \geq 2$ is:↵
↵
$f(x, l) := C(C-1)(\sum\limits_{j=1}^\infty x^j)^2(\sum\limits_{j=1}^{K-2}x^j + \sum\limits_{j=K-1}^\infty (C-1)x^j)^{l-2} \tag{1}$. ↵
↵
The $C$ is because the first segment has $C$ choices.↵
↵
The $C-1$ is because the second segment always has $C-1$ choices.↵
↵
The $(\sum\limits_{j=1}^{K-2}x^j + \sum\limits_{j=K-1}^\infty (C-1)x^j)^{l-2}$ contain two parts: $x^j$ encodes the length of segment $i$ ($2 \leq i \leq i-1$). $1$, and $C-1$ encode the transfer contribution between $i \rightarrow i+1$. If $len(S_i) \leq K-2$, then $S_{i+1}$ has only 1 choice (See (2)). Otherwise, $S_{i+1}$ has $C-1$ choices. ↵
↵
Now we have dealt with the length of $S_i (2 \leq i \leq l-1)$ and the transfer contribution between $i$ and $i+1$ ($2 \leq i \leq l-1$). But we still omit two things: The length of head and tail! So we encode each of them with $\sum\limits_{j=1}^\infty x^j$. See the below picture: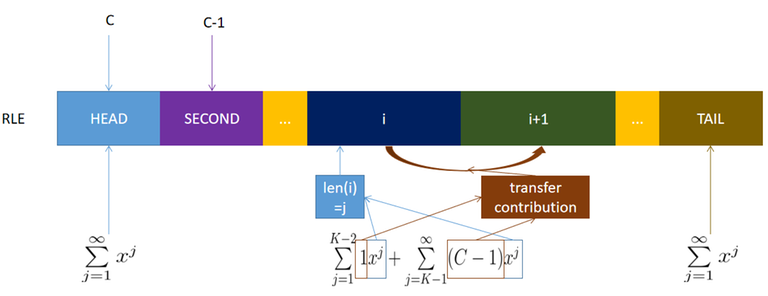↵
↵
$\sum\limits_{j=1}^\infty x^j=\frac{x}{1-x} \tag{2}$.↵
↵
$\sum\limits_{j=1}^{K-2}x^j + \sum\limits_{j=K-1}^\infty (C-1)x^j = \frac{x-x^{K-1}}{1-x} + (C-1)\frac{x^{K-1}}{1-x} = \frac{x+(C-2)x^{K-1}}{1-x} \tag{3}$.↵
↵
And put $(1), (2), (3)$ together, $f(x, l)=C(C-1)\frac{x^2}{(1-x)^2}(\frac{x+(C-2)x^{K-1}}{1-x})^{l-2} \tag{4}$.↵
↵
Here you might get confused: Will sum to infinite, e.g., $\sum\limits_{j=1}^\infty x^j$, lead to overflow (i.e., contain terms whose orders are higher than $x^N$)? The answer is YES, but we are not afraid of it. This answer refers to a core idea of GFs: I only care about $[x^N]f(x, l)$, because the sum of segments should be $N$. For the terms higher than $x^N$, I don't fxxking care about it!!! It is quite magic that, including more terms may decrease the computational complexity! If you are curious about it, you might read the English [tutorial](https://math.stackexchange.com/questions/4586327/sum-of-product-of-min-which-is-related-to-the-pentagonal-number-theorem) of 279Ex carefully. That is because summing more terms might lead to closed-form expressions which are easier to compute. However, we should be cautious about the low terms. For example, If we mistake $\sum\limits_{j=1}^\infty x^j$ for $\sum\limits_{j=0}^\infty x^j$, we will get into big trouble as we count the contribution of "empty segments" that should not be counted. So, for GF methods, overflowing parts are not important, but we should be careful about the correctness of the non-overflowing parts, especially the low-order terms.↵
↵
Now, to take all possible length $l \geq 2$ into consideration, we sum $f(x, l)$ over $l$:↵
↵
$g(x) := \sum\limits_{l=2}^\infty f(x, l) = \sum\limits_{l=2}^\infty C(C-1)\frac{x^2}{(1-x)^2}(\frac{x+(C-2)x^{K-1}}{1-x})^{l-2} \tag{5}$↵
↵
And, ↵
↵
$\sum\limits_{l=0}^\infty(\frac{x+(C-2)x^{K-1}}{1-x})^{l} = \frac{1}{1-\frac{x+(C-2)x^{K-1}}{1-x}} = \frac{1-x}{1-2x-(C-2)x^{K-1}} \tag{6}$↵
↵
Combining (5), (6): ↵
↵
$g(x) = \frac{C(C-1)x^2}{(1-x)(1-2x-(C-2)x^{K-1})} \tag{7}$.↵
↵
The denominator of $g(x)$ is $(C-2)x^K - (C-2)x^{K-1} + 2x^2 - 3x + 1$. We care about $[x^N]g(x) = [x^{N-2}]\frac{C(C-1)}{(C-2)x^K - (C-2)x^{K-1} + 2x^2 - 3x + 1}$. The thing we care about is "polynomial inversion", which could be computed using FFT/NTT in $O(NlogN)$ time. Here is a useful summation: [Operations on Formal Power Series](https://codeforces.me/blog/entry/56422). Formally, if you want to compute $[x^k]\frac{1}{A(x)}$, we need to find a $B(x) (deg(B(x)) \leq k)$ such that $A(x)B(x) \equiv 1 (\mod x^{k+1})$, and $[x^k]\frac{1}{A(x)} = [x^k]B(x)$.↵
↵
Submission: https://atcoder.jp/contests/abc279/submissions/36865779↵
↵
Core code (with explanation):↵
↵
~~~~~↵
int main(void){↵
int n, k, c; cin >> n >> k >> c;↵
poly<998244353> x, xinv; //define two polynomials↵
x.a.resize(n-1); //We want to get [x^{N-2}](1/((C-2)x^K - (C-2)x^{K-1} + 2x^2 - 3x + 1)), so the inversion should be set to n-1↵
if(n-1 > 0) x.a[0] += 1;↵
if(n-1 > 1) x.a[1] -= 3;↵
if(n-1 > 2) x.a[2] += 2; ↵
if(n-1 > k-1) x.a[k-1] -= poly<998244353>::mint(c-2);↵
if(n-1 > k) x.a[k] += poly<998244353>::mint(c-2); //remember to use += instead of =, as k and/or k-1 may equal to 0, 1, 2↵
xinv = x.inverse(n-1); //Inverse!↵
cout << (c + ((1ll*c*(c-1))%998244353)*xinv[n-2]())%998244353 << "\n"; //Care about integer overflow! Remember to add c for the case where l==1.↵
}↵
~~~~~↵
↵
↵
↵
[Atcoder Beginner Contest 279](https://atcoder.jp/contests/abc279) is good for learning [generating functions (GFs)](https://en.wikipedia.org/wiki/Generating_function). The English version tutorial of [279Ex](https://atcoder.jp/contests/abc279/tasks/abc279_h) has already been posted on the [MathStackExchange](https://math.stackexchange.com/questions/4586327/sum-of-product-of-min-which-is-related-to-the-pentagonal-number-theorem) by a kind person. Unfortunately, the English tutorial on [279G](https://atcoder.jp/contests/abc279/tasks/abc279_g) is not available. Now I would like to make a second-hand tutorial on [279G](https://atcoder.jp/contests/abc279/tasks/abc279_g) based on [PCTprobability's idea](https://atcoder.jp/contests/abc279/editorial/5293). I spend a huge amount of time understanding this idea. For contestants at about my level, it is quite difficult to understand ↵
[the idea](https://atcoder.jp/contests/abc279/editorial/5293) even if it is written in English, let alone it is written in Japanese only (My Japanese is N5 level). I will make the following contributions. ↵
↵
(1)Write the tutorial in English. The original tutorial is in Japanese only. ↵
↵
(2)Fill in the details. I believe you can understand my words.↵
↵
(3)Offer an accepted implementation.↵
↵
I have to state that, using generating function is definitely not the best way to solve this problem. It could be solved much simpler by using dynamic programming with [monotone deque optimization](https://robert1003.github.io/2020/02/16/dp-opt-monotone-queue.html). However, this problem is also a good chance to learn [generating functions (GFs)](https://en.wikipedia.org/wiki/Generating_function). Generating functions encode the information of sequences in a continuous way. If you do not know anything about GFs, I suggest you read:↵
↵
(1) How to use GFs to solve recurrence? [Link](https://math.stackexchange.com/questions/1544784/generating-functions-recurrence-relations).↵
↵
(2) How to prove the Vandemonde convolution identity using GFs? [Link](https://math.stackexchange.com/questions/3494228/proof-vandermondes-identity-using-generating-function).↵
↵
(3) And most relevant to this problem, how to solve partitions using GFs? [Link](https://en.wikipedia.org/wiki/Pentagonal_number_theorem).↵
↵
The most important notation $\[x^k\]f(x)$ denotes the coefficient of $x^k$ in function $f(x)$. For example, $\[x^2\](x^3+2x^2+1)=2$. And $\[x^2\]\frac{1}{1-2x}=4$, because we can expand $\frac{1}{1-2x}$ to $\sum\limits_{i=0}^\infty (2x)^i$ in the region of convergence $(-\frac{1}{2}, \frac{1}{2})$. So the coefficient of $x^2$ is $4$. ↵
↵
**Part2: Problem Statement**↵
↵
[The problem](https://atcoder.jp/contests/abc279/tasks/abc279_g) says: ↵
There is a grid with $1×N$ squares, numbered $1,2,…,N$ from left to right.↵
↵
Takahashi prepared paints of $C$ colors and painted each square in one of the C colors.↵
Then, there were at most two colors in any consecutive K squares.↵
Formally, for every integer $i$ such that $1≤i≤N−K+1$, there were at most two colors in squares $i,i+1,…,i+K−1$.↵
↵
In how many ways could Takahashi paint the squares?↵
Since this number can be enormous, find it modulo $998244353$.↵
↵
$\cdot \text{All inputs are integers.}$↵
↵
$\cdot 2 \leq K \leq N \leq 10^6$.↵
↵
$\cdot 1 \leq C \leq 10^9$.↵
↵
Test Case $1$: $N=K=C=3$. In this input, we have a $1×3$ grid. Among the $27$ ways to paint the squares, there are $6$ ways to paint all squares in different colors, and the remaining $21$ ways are such that there are at most two colors in any consecutive three squares.↵
↵
Test Case $2$: $N=10, K=5, C=2$: Print $1024$.↵
↵
Test Case $3$: $N=998, K=244, C=353$: Print $952364159$.↵
↵
**Part3: Idea**↵
↵
(1) What are GFs good at? Gf is good at solving partitions, for example, the [Pentagonal number theorem](https://en.wikipedia.org/wiki/Pentagonal_number_theorem). So, the first step is to compress the colors by [Run-Length Encoding (RLE)](https://en.wikipedia.org/wiki/Run-length_encoding). For example, if the colors are $(1,1,1,2,2,3,2,2)$, then they are uniquely compressed to $((1, 3), (2, 2), (3, 1), (2, 2))$. With RLE, $[1, n]$ is **partitioned** into $l$ segments with different colors. Let me denote these segments as $S_1, S_2, ..., S_l$. Please note that adjacent segments must be painted with different colors, otherwise you can merge the adjacent segments into one, which violates the definition of RLE. The idea to divide the interval into segments for counting also appears in Pinely Round Problem D.↵
↵
(2)Consider $2 \leq i \leq l-1$. If $|S_i| \leq K-2$, then $S_{i+1}$ only has one choice: Paint it with the same color as $S_{i-1}$. Otherwise, the last element of $S_{i-1}$, the whole segment $S_{i}$ and the first element of $S_{i+1}$ will form an interval with size $\leq K$ and three colors, violating the rule. If $|S_i| > K-2$, then $S_{i+1}$ has $C-1$ choices. It is only required that the color of $S_{i+1}$ is different from that of $S_{i}$.↵
↵
(3)I claim that the generating function for segmentation of length $l \geq 2$ is:↵
↵
$f(x, l) := C(C-1)(\sum\limits_{j=1}^\infty x^j)^2(\sum\limits_{j=1}^{K-2}x^j + \sum\limits_{j=K-1}^\infty (C-1)x^j)^{l-2} \tag{1}$. ↵
↵
The $C$ is because the first segment has $C$ choices.↵
↵
The $C-1$ is because the second segment always has $C-1$ choices.↵
↵
The $(\sum\limits_{j=1}^{K-2}x^j + \sum\limits_{j=K-1}^\infty (C-1)x^j)^{l-2}$ contain two parts: $x^j$ encodes the length of segment $i$ ($2 \leq i \leq i-1$). $1$, and $C-1$ encode the transfer contribution between $i \rightarrow i+1$. If $len(S_i) \leq K-2$, then $S_{i+1}$ has only 1 choice (See (2)). Otherwise, $S_{i+1}$ has $C-1$ choices. ↵
↵
Now we have dealt with the length of $S_i (2 \leq i \leq l-1)$ and the transfer contribution between $i$ and $i+1$ ($2 \leq i \leq l-1$). But we still omit two things: The length of head and tail! So we encode each of them with $\sum\limits_{j=1}^\infty x^j$. See the below picture:↵
↵
$\sum\limits_{j=1}^\infty x^j=\frac{x}{1-x} \tag{2}$.↵
↵
$\sum\limits_{j=1}^{K-2}x^j + \sum\limits_{j=K-1}^\infty (C-1)x^j = \frac{x-x^{K-1}}{1-x} + (C-1)\frac{x^{K-1}}{1-x} = \frac{x+(C-2)x^{K-1}}{1-x} \tag{3}$.↵
↵
And put $(1), (2), (3)$ together, $f(x, l)=C(C-1)\frac{x^2}{(1-x)^2}(\frac{x+(C-2)x^{K-1}}{1-x})^{l-2} \tag{4}$.↵
↵
Here you might get confused: Will sum to infinite, e.g., $\sum\limits_{j=1}^\infty x^j$, lead to overflow (i.e., contain terms whose orders are higher than $x^N$)? The answer is YES, but we are not afraid of it. This answer refers to a core idea of GFs: I only care about $[x^N]f(x, l)$, because the sum of segments should be $N$. For the terms higher than $x^N$, I don't fxxking care about it!!! It is quite magic that, including more terms may decrease the computational complexity! If you are curious about it, you might read the English [tutorial](https://math.stackexchange.com/questions/4586327/sum-of-product-of-min-which-is-related-to-the-pentagonal-number-theorem) of 279Ex carefully. That is because summing more terms might lead to closed-form expressions which are easier to compute. However, we should be cautious about the low terms. For example, If we mistake $\sum\limits_{j=1}^\infty x^j$ for $\sum\limits_{j=0}^\infty x^j$, we will get into big trouble as we count the contribution of "empty segments" that should not be counted. So, for GF methods, overflowing parts are not important, but we should be careful about the correctness of the non-overflowing parts, especially the low-order terms.↵
↵
Now, to take all possible length $l \geq 2$ into consideration, we sum $f(x, l)$ over $l$:↵
↵
$g(x) := \sum\limits_{l=2}^\infty f(x, l) = \sum\limits_{l=2}^\infty C(C-1)\frac{x^2}{(1-x)^2}(\frac{x+(C-2)x^{K-1}}{1-x})^{l-2} \tag{5}$↵
↵
And, ↵
↵
$\sum\limits_{l=0}^\infty(\frac{x+(C-2)x^{K-1}}{1-x})^{l} = \frac{1}{1-\frac{x+(C-2)x^{K-1}}{1-x}} = \frac{1-x}{1-2x-(C-2)x^{K-1}} \tag{6}$↵
↵
Combining (5), (6): ↵
↵
$g(x) = \frac{C(C-1)x^2}{(1-x)(1-2x-(C-2)x^{K-1})} \tag{7}$.↵
↵
The denominator of $g(x)$ is $(C-2)x^K - (C-2)x^{K-1} + 2x^2 - 3x + 1$. We care about $[x^N]g(x) = [x^{N-2}]\frac{C(C-1)}{(C-2)x^K - (C-2)x^{K-1} + 2x^2 - 3x + 1}$. The thing we care about is "polynomial inversion", which could be computed using FFT/NTT in $O(NlogN)$ time. Here is a useful summation: [Operations on Formal Power Series](https://codeforces.me/blog/entry/56422). Formally, if you want to compute $[x^k]\frac{1}{A(x)}$, we need to find a $B(x) (deg(B(x)) \leq k)$ such that $A(x)B(x) \equiv 1 (\mod x^{k+1})$, and $[x^k]\frac{1}{A(x)} = [x^k]B(x)$.↵
↵
Submission: https://atcoder.jp/contests/abc279/submissions/36865779↵
↵
Core code (with explanation):↵
↵
~~~~~↵
int main(void){↵
int n, k, c; cin >> n >> k >> c;↵
poly<998244353> x, xinv; //define two polynomials↵
x.a.resize(n-1); //We want to get [x^{N-2}](1/((C-2)x^K - (C-2)x^{K-1} + 2x^2 - 3x + 1)), so the inversion should be set to n-1↵
if(n-1 > 0) x.a[0] += 1;↵
if(n-1 > 1) x.a[1] -= 3;↵
if(n-1 > 2) x.a[2] += 2; ↵
if(n-1 > k-1) x.a[k-1] -= poly<998244353>::mint(c-2);↵
if(n-1 > k) x.a[k] += poly<998244353>::mint(c-2); //remember to use += instead of =, as k and/or k-1 may equal to 0, 1, 2↵
xinv = x.inverse(n-1); //Inverse!↵
cout << (c + ((1ll*c*(c-1))%998244353)*xinv[n-2]())%998244353 << "\n"; //Care about integer overflow! Remember to add c for the case where l==1.↵
}↵
~~~~~↵
↵
↵





