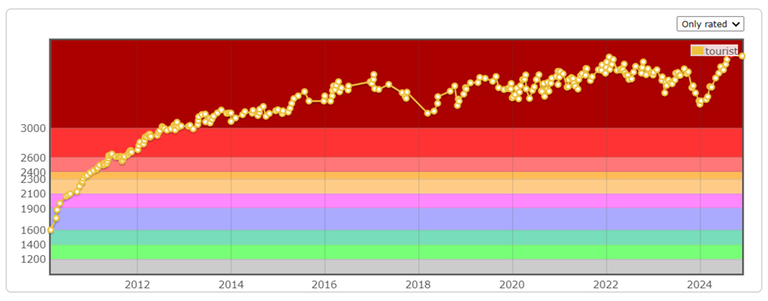
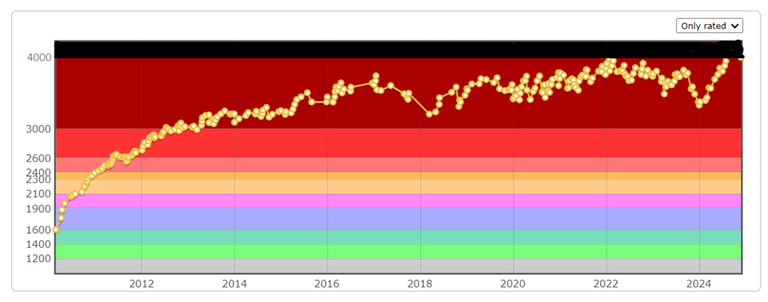
This blog will be useful for all those who never achieved Master but really wants to. Based on my experience, you can achieve Master by doing these steps:
Become GM on your main account
Create an alt and smurf Div.2+ contests until you reach Master.
...
PROFIT!
Hope it helps, codeforcers!