C++ has always had the convenient data structures std::set and std::map, which are tree data structures whose operations take  time. With C++11, we finally received a hash set and hash map in
time. With C++11, we finally received a hash set and hash map in std::unordered_set and std::unordered_map. Unfortunately, I've seen a lot of people on Codeforces get hacked or fail system tests when using these. In this post I'll explain how it's possible to break these data structures and what you can do in order to continue using your favorite hash maps without worrying about being hacked
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
16:23:08
Register now »
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
After Round 512 finished, I took a look at the rating changes from Div 1 and ended up calculating their average.
To my surprise, the sum of the rating changes was -5383 (anyone want to help double check the math?). This means that for the 500 participants the average rating change was -10.77. I know this contest is probably an outlier, but this seems way too extreme to be reasonable.
If anything, I think the average rating change ought to be slightly positive, in order to reward participation over time. For example if the average rating change per contest is +0.5, then if someone participates in 100 contests over two years (which is some serious dedication), the most this could contribute to their rating is +50, which seems perfectly fine. This also serves as encouragement for relatively inactive people to be more active.
However, averaging more than a 10-point loss in a round is unreasonable and likely to discourage people over time from participating if it keeps happening; i.e., people who maintain a similar level of performance will see their rating go down over time, and people who improve slightly will see their rating stay flat. If my calculations all check out, the rating algorithm likely deserves some reconsideration.
EDIT: After some more observation, it looks like what's happening is that new accounts who do just a few contests, lose rating to everyone else, and go inactive are potentially offsetting this effect overall. It's hard to say for sure without more specific data.
Hi Codeforces! In Round 507 earlier today, a large number of "mostly correct" randomized solutions on 1039B - Subway Pursuit were hacked. I wanted to write a quick explanation of how it's possible to hack these, as well as a guide on how to write your code so that you aren't vulnerable to getting hacked.
First to go over the solution quickly (skip down a few paragraphs if you already know the solution): one can use binary search to reduce the range of possible locations for the train to a constant multiple of K, such as 6K. Just make sure to expand out both ends of the range by K after every iteration. Once the range is at most 6K, one can repeat the following:
1) Make a random guess out of the remaining numbers. The probability of success is at least 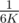 .
.
2) Binary search again until the range is at most 6K again. It turns out this only takes one query, since after our previous guess our 6K range will become an 8K range, and a single query will reduce this to 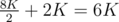 again.
again.
Since K ≤ 10 and we have 4500 queries, this works because our probability of failure on any test case is at most 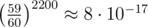 , extremely low.
, extremely low.
However, this makes a key assumption that the train locations are independent of your queries. The main problem that most hacked solutions had was being completely deterministic; i.e., the programs query the same sequence of numbers on every run, given the same output. Most people had this issue due to using rand() without ever calling srand(). There were a few other causes as well: random_device is oddly deterministic on Codeforces, as is mt19937 without a seed. Calling srand() with a fixed value is no good either, as the program is still totally predictable.
Because of the predictability, these programs are quite easy to hack: simply generate the same sequence of queries that the program would make, and set up the train to always be at a different location from each query. To make this even easier for yourself when hacking, you can choose N = 2 and K = 1, which skips the initial binary search phase, and then literally move the train to the non-queried option between 1 and 2 every time.
Workaround?
To get around this, many competitors seeded their generators with the current time by calling srand(time(NULL)); This stops the code from being deterministic and makes it less likely you will get hacked, but it turns out this is still very possible to hack. How? The main problem here is that time(NULL) is only precise to one second. So if I'm able to guess the second that your program gets run, your program is effectively deterministic.
It turns out I don't even need to guess. If I set up N = 11 and K = 10, I can produce all the different query sequences you might generate in the next 10 seconds, since your code will almost certainly be run a few seconds after my generator. Then for every query, at least one of the 11 positions will not be chosen by any of the 10 sequences, and I can move the train to that position each time. Unfortunately -- or fortunately for the people in my room ;) -- I didn't have time to do this during the contest.
Solution
The fix is quite easy. time(NULL) has the right idea, but we should use a much more high-precision clock:
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
Then generate random numbers by calling rng(). Remember to include <chrono> and <random> for this.
- Why didn't I use
rand()/srand()? See this post: Don't use rand()
Another option is to use the address of a newly allocated heap variable:
mt19937 rng((uint64_t) new char);
This should be different every run. Note this creates a tiny memory leak for the life of the program since we never call delete, but since it's just one variable it's not a big deal.
I personally like to combine both of these methods, but it isn't necessary. Either one will give your program much more unpredictability, making it effectively impossible to hack.
Thanks for reading! This will likely lead to me getting fewer hacks in the future, but I thought the community should have a guide explaining this unusual situation.
If you want to read more, take a look at dacin21's great post on anti-hash tests.
Don't use rand(). Why? Let's jump right into some code. What value will the following code print, approximately?
#include <cstdlib>
#include <iostream>
using namespace std;
const int ITERATIONS = 1e7;
int main() {
double sum = 0;
for (int i = 0; i < ITERATIONS; i++)
sum += rand() % 1000000;
cout << "Average value: " << sum / ITERATIONS << '\n';
}
Should be about 500,000, right? Turns out it depends on the compiler, and on Codeforces it prints 16382, which isn't even close. Try it out yourself.
What's happening here?
If you look up C++ documentation on rand(), you'll see that it returns "a pseudo-random integral value between 0 and RAND_MAX." Click again on RAND_MAX and you'll see that "This value is implementation dependent. It's guaranteed that this value is at least 32767." On the Codeforces machines, it turns out RAND_MAX is exactly 32767. That's so small!
It doesn't stop there though; random_shuffle() also uses rand(). Recall that in order to perform a random shuffle, we need to generate random indices up to n, the size of the array. But if rand() only goes up to 32767, what happens if we call random_shuffle() on an array with significantly more elements than that? Time for some more code. What would you expect the following code to print?
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
const int N = 3000000;
double average_distance(const vector<int> &permutation) {
double distance_sum = 0;
for (int i = 0; i < N; i++)
distance_sum += abs(permutation[i] - i);
return distance_sum / N;
}
int main() {
vector<int> permutation(N);
for (int i = 0; i < N; i++)
permutation[i] = i;
random_shuffle(permutation.begin(), permutation.end());
cout << average_distance(permutation) << '\n';
}
This computes the average distance that each value moves in the random shuffle. If you work out a bit of math, you'll find that the answer on a perfectly random shuffle should be 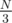 = 1,000,000. Even if you don't want to do the math, you can observe that the answer is between
= 1,000,000. Even if you don't want to do the math, you can observe that the answer is between 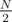 = 1,500,000, the average distance for index 0, and
= 1,500,000, the average distance for index 0, and 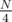 = 750,000, the average distance for index
= 750,000, the average distance for index 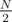 .
.
Well, once again the code above disappoints; it prints out 64463. Try it yourself. In other words, random_shuffle() moved each element a distance of 2% of the length of the array on average. Based on my testing, the implementation of random_shuffle() on Codeforces matches the following exactly:
for (int i = 1; i < N; i++)
swap(permutation[i], permutation[rand() % (i + 1)]);
So naturally if RAND_MAX is much less than N, this shuffle will be problematic.
rand() itself has more quality problems than just RAND_MAX being small though; it is typically implemented as a relatively simple linear congruential generator. On the Codeforces compiler, it looks like this:
static long holdrand = 1L;
void srand(unsigned int seed) {
holdrand = (long) seed;
}
int rand() {
return (((holdrand = holdrand * 214013L + 2531011L) >> 16) & 0x7fff);
}
In particular, linear congruential generators (LCGs) suffer from extreme predictability in the lower bits. The k-th bit (starting from k = 0, the lowest bit) has a period of at most 2k + 1 (i.e., how long until the sequence takes to repeat). So the lowest bit has a period of just 2, the second lowest a period of 4, etc. This is why the function above discards the lowest 16 bits, and the resulting output is at most 32767.
What's the solution?
Don't worry, as of C++11 there are much better random number generators available in C++. The only thing you need to remember is to use mt19937, included in the <random> header. This is a Mersenne Twister based on the prime 219937 - 1, which also happens to be its period. It's a much higher-quality RNG than rand(), in addition to being much faster (389 ms to generate and add 108 numbers from mt19937 in Custom Invocation, vs. 1170 ms for rand()). It also produces full 32-bit unsigned outputs between 0 and 232 - 1 = 4294967295, rather than maxing out at a measly 32767.
To replace random_shuffle(), you can now call shuffle() and pass in your mt19937 as the third argument; the shuffle algorithm will use your provided generator for shuffling.
C++11 also gives you some nifty distributions. uniform_int_distribution gives you perfectly uniform numbers, without the bias of mod -- i.e., rand() % 10000 is more likely to give you a number between 0 and 999 than a number between 9000 and 9999, since 32767 is not a perfect multiple of 10000. There are many other fun distributions as well including normal_distribution and exponential_distribution.
To give you a more concrete idea, here's some code using several of the tools mentioned above. Note that the code seeds the random number generator using a high-precision clock. This is important for avoiding hacks specifically tailored to your code, since using a fixed seed means that anyone can determine what your RNG will output. For more details, see How randomized solutions can be hacked, and how to make your solution unhackable.
One last thing: if you want 64-bit random numbers, just use mt19937_64 instead.
#include <algorithm>
#include <chrono>
#include <iostream>
#include <random>
#include <vector>
using namespace std;
const int N = 3000000;
double average_distance(const vector<int> &permutation) {
double distance_sum = 0;
for (int i = 0; i < N; i++)
distance_sum += abs(permutation[i] - i);
return distance_sum / N;
}
int main() {
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
vector<int> permutation(N);
for (int i = 0; i < N; i++)
permutation[i] = i;
shuffle(permutation.begin(), permutation.end(), rng);
cout << average_distance(permutation) << '\n';
for (int i = 0; i < N; i++)
permutation[i] = i;
for (int i = 1; i < N; i++)
swap(permutation[i], permutation[uniform_int_distribution<int>(0, i)(rng)]);
cout << average_distance(permutation) << '\n';
}
Both shuffles result in almost exactly 106 average distance, like we originally expected.
Additional References
This post was inspired in part by Stephan T. Lavavej's talk "rand() Considered Harmful": https://channel9.msdn.com/Events/GoingNative/2013/rand-Considered-Harmful
If you want even faster, higher-quality random number generators, take a look at this site by Sebastiano Vigna.
Thanks to the many authors of this contest (all eight of them) for a great set of problems! I'll sketch out the solution ideas for a few of them here:
1019A - Elections
Let's assume our goal is to end the election with v votes and determine the minimum cost to do so.
First, we need to make sure every other party ends up with fewer than v votes. To do this, we should bribe enough people in every party to get them down to v - 1 votes or fewer. We can do this greedily by bribing the cheapest people in the party.
After that if we have v votes (or more), we are done. Otherwise, we should repeatedly bribe the cheapest voters remaining until we get to v. Note that we can do this in O(n) time rather than  by using an O(n) selection algorithm such as nth_element, though this wasn't necessary to pass the problem.
by using an O(n) selection algorithm such as nth_element, though this wasn't necessary to pass the problem.
Finally, simply loop over all possible values of v and take the minimum cost across all of them for an O(n2) solution.
Code: 41475525
In fact it is even possible to solve the problem in  . Here is a solution using ternary search on v: 41534204
. Here is a solution using ternary search on v: 41534204
1019B - The hat
Let 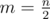 . Let's define the function d(i) = ai - ai + m. We are looking for i such that d(i) = 0. Notice that since |ai - ai + 1| = 1, d(i) - d(i + 1) must be - 2, 0, or 2.
. Let's define the function d(i) = ai - ai + m. We are looking for i such that d(i) = 0. Notice that since |ai - ai + 1| = 1, d(i) - d(i + 1) must be - 2, 0, or 2.
First query for the value of d(1). If it is odd, then every d(i) is odd due to our property above, so the answer is - 1. Otherwise every value d(i) is even. Notice that d(m + 1) = am + 1 - a1 = - d(1). This means that one of d(1) and d(m + 1) is a positive even value, and the other is a negative even value. Since consecutive values can only differ by - 2, 0, or 2, there must be an index i in between 1 and m + 1 that satisfies d(i) = 0, and we can use binary search to find this index.
Code: 41502076
: 1019D - Large Triangle
The obvious solution for this problem is O(n3), which can actually be squeezed in the time limit if you're careful; e.g., 41488961 and 41491248. However the real solution is  , which I'll describe here:
, which I'll describe here:
Since the area of a triangle is 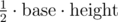 , if we picked two of the n points as our base, we would know exactly what height we needed in order to make a triangle with the goal area. In particular, if we had our points sorted by distance to this segment, we could use binary search to determine whether or not there was such a point in
, if we picked two of the n points as our base, we would know exactly what height we needed in order to make a triangle with the goal area. In particular, if we had our points sorted by distance to this segment, we could use binary search to determine whether or not there was such a point in  time.
time.
We can perform a rotational sweep on the set of points, which lets us set up this height-sorted list for every segment in order to solve the problem. (Imagine smoothly rotating the points clockwise, stopping whenever any two points are perfectly lined up horizontally.)
To do this we can take all n2 segments and sort them by angle. We also initialize our sorted list of points by y, breaking ties by x. We then iterate through our sorted segment list, swapping two points each time in order to maintain the height-sorted list. Finally we do two binary searches per segment to find if there are any points at the appropriate height (one above and one below).
Note that we can perform all these computations in integers only by using cross products. See the code below for details. Also, kudos to the problem writers for adding the guarantee that "no three cities lie on the same line," which helps keep the code cleaner without changing the key idea of the problem.
Code: 41502172
Unfortunately I don't know the solutions for C or E. If you do, leave a comment!
I've run the following test case on several of the accepted submissions for 1017E - The Supersonic Rocket, and more than a third of them get the answer wrong:
4 4
0 0
1 0
1 1
2 1
0 1
1 1
1 0
2 0
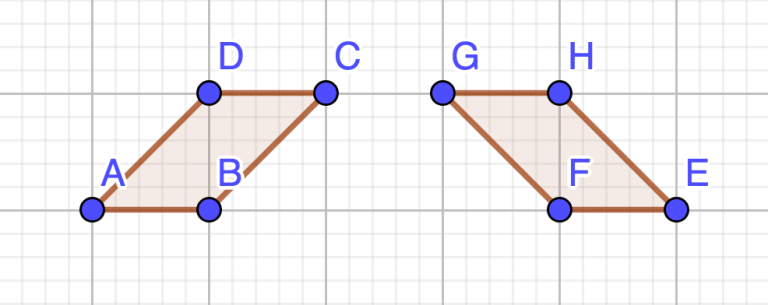
The answer is NO since the two polygons are rotationally distinct (they are reflections of each other), but many of the accepted submissions output YES--for example:
ko_osaga https://codeforces.me/contest/1017/submission/41350783
geniucos https://codeforces.me/contest/1017/submission/41375712
Benq https://codeforces.me/contest/1017/submission/41354131
Swistakk https://codeforces.me/contest/1017/submission/41351667
(Try running them yourself using Custom Invocation)
Here's why they get it wrong:
After computing the convex hulls of the two sets of points, the problem boils down to determining if two convex polygons are isomorphic under rotation and translation (that is, whether they can be made the same after rotating and translating).
One strategy for this is building up the string "edge length, angle, edge length, angle, ..." for each polygon and seeing if the two strings are identical after some cyclic rotation. However since computing floating-point angle values is error-prone, one idea is to keep all computations in integers by using the cross product of the two edges that make the angle instead of the angle itself. This serves as a proxy for the angle θ since 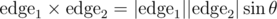 , and the solutions above use this idea.
, and the solutions above use this idea.
Unfortunately, sin θ doesn't quite uniquely identify θ, since 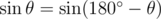 . The case above makes use of this fact by alternating angles of
. The case above makes use of this fact by alternating angles of  and
and  , making all cross products the same despite angles being different.
, making all cross products the same despite angles being different.
Now what?
Fortunately there is a nice fix; instead of the cross product we can use the dot product, which does the trick because 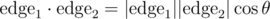 , and cos θ is unique for
, and cos θ is unique for 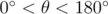 (our polygons are convex). A similar idea that also works is to use the distance between vertex i and vertex i + 2, which also uniquely identifies the angle when convex (thanks scott_wu and ecnerwala for discussing).
(our polygons are convex). A similar idea that also works is to use the distance between vertex i and vertex i + 2, which also uniquely identifies the angle when convex (thanks scott_wu and ecnerwala for discussing).
For non-convex polygons we can use the combination of edge length, cross product, and dot product (try to convince yourself why this is sufficient), which again enables us to specify the polygon precisely using only integers.
I'm unable to do weekday rounds all summer, and there are probably others with a similar situation.
| Name |
|---|









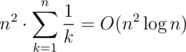 .
.