I've run the following test case on several of the accepted submissions for 1017E - The Supersonic Rocket, and more than a third of them get the answer wrong:
4 4
0 0
1 0
1 1
2 1
0 1
1 1
1 0
2 0
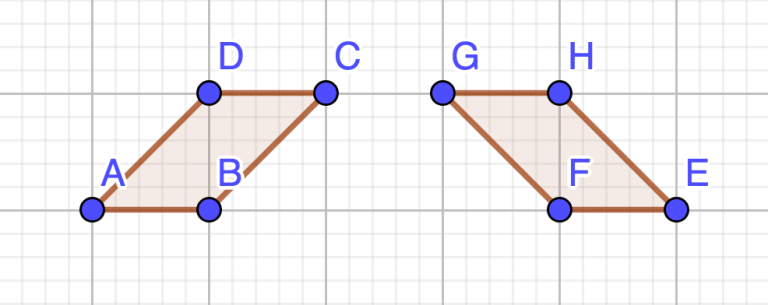
The answer is NO since the two polygons are rotationally distinct (they are reflections of each other), but many of the accepted submissions output YES--for example:
ko_osaga https://codeforces.me/contest/1017/submission/41350783
geniucos https://codeforces.me/contest/1017/submission/41375712
Benq https://codeforces.me/contest/1017/submission/41354131
Swistakk https://codeforces.me/contest/1017/submission/41351667
(Try running them yourself using Custom Invocation)
Here's why they get it wrong:
After computing the convex hulls of the two sets of points, the problem boils down to determining if two convex polygons are isomorphic under rotation and translation (that is, whether they can be made the same after rotating and translating).
One strategy for this is building up the string "edge length, angle, edge length, angle, ..." for each polygon and seeing if the two strings are identical after some cyclic rotation. However since computing floating-point angle values is error-prone, one idea is to keep all computations in integers by using the cross product of the two edges that make the angle instead of the angle itself. This serves as a proxy for the angle θ since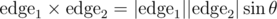 
, and the solutions above use this idea.
Unfortunately, sin θ doesn't quite uniquely identify θ, since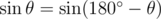 
. The case above makes use of this fact by alternating angles of 
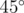and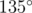 
, making all cross products the same despite angles being different.
Now what?
Fortunately there is a nice fix; instead of the cross product we can use the dot product, which does the trick because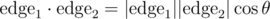 
, and cos θ is unique for 
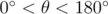(our polygons are convex). A similar idea that also works is to use the distance between vertex i and vertex i + 2, which also uniquely identifies the angle when convex (thanks scott_wu and ecnerwala for discussing).
For non-convex polygons we can use the combination of edge length, cross product, and dot product (try to convince yourself why this is sufficient), which again enables us to specify the polygon precisely using only integers.
Of course, no offense to ko_osaga / geniucos / Benq / Swistakk; my in-contest code was incorrect for a similar reason :)
It's funny cause I even thought of reflection and actually considered reflection as a valid rotation (and initially I was running 2 KMPs, 4th line from the end of my code). I then realized it's wrong and thought my code is flawless after ACing. Thanks for letting me (and others like me) know about the issue:)
My solution (which only do 90 degree rotation to check isomorphism and handle n = 2 separately) get WA on this test case:
What if you did some O(nm) algorithm for n*m<=1e7 and 90 degree turns otherwise?
You can easily make two congruent polygons which are not a 90 degree rotation.
Take a large convex polygon, multiply each of its coordinates by 5 for polygon 1. For polygon 2, rotate this by the same angle that sends (5,0) to (4,3).
This is a great lesson to learn, thank you very much!
According to the editorial, it seems like author Magolor's code also fails your test. If that was the one used for hack, then it would've been unrated for any means XD
But seems that Kostroma's solution works well. (He is one of the testers)
Anyway, it's unrated now.┑(￣_￣)┍
Exactly what I realized while pending system test :)
I submitted 41371099 using dot product just after I surprisingly found my in-contest code using cross product passed the system test, with exactly the same test case as which in this blog in the comment at the end of the code :)
This is even simpler, forget about cross/dot products!
This is nice, but you won't be able to do much in geometry if cross/dot product is something fancy for you :P
Cross product is fancy for me :'(
I have just read your blog.
The following integer number based up solving passed your tricky test case.
41412779
Graham's scan algorithm is used to compute the convex hull. The isomorphism checking uses integer numbers based on the idea suggested in the editorial to generate a [edge,angle] signature vector for each convex polygon. The modulo division operator is used to iterate through one of the two signatures instead of duplicating it.
Here's another way to think about this (although in the end it's not much different):
Given three vertices a, b, c (thought of as complex numbers), the angle at b is really the argument of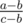
. The problem is that the argument can be irrational. But 
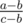has rational real and imaginary part, so there is no need to take the argument: Just compute 
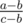(using 
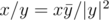, and maybe reducing the fraction to make sure the representation is canonical).
Now you don't just get the angle at b, but also the ratio between the side lengths. So this allows you to check if the hulls are similar (i.e. allowing scaling, but not reflection), and then you just need to check some quantity that does change under scaling, e.g. area or longest side length.
So you end up storing 3 integers, and it is exactly the same as storing distance, cross and dot products.