CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
15:40:35
Зарегистрироваться »
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Привет, Codeforces!
18 декабря 2016 года в 13:35 MSK состоится очередной раунд Codeforces #386 для участников из второго дивизиона. Традиционно, участники из первого дивизиона приглашаются поучаствовать в соревновании вне конкурса. Обратите внимание на необычное время начала раунда!
Этот раунд проводится по задачам муниципального этапа Всероссийской олимпиады школьников по информатике 2016/2017 года г. Саратова. Задачи были подготовлены силами Центра олимпиадной подготовки программистов Саратовского ГУ.
Хотелось бы сказать большое спасибо Николаю Калинину (KAN) за помощь в подготовке задач, Татьяне Семеновой (Tatiana_S) за перевод условий на английский, Михаилу Мирзаянову (MikeMirzayanov) за замечательные системы Codeforces и Polygon, а также Владимиру Петрову (vovuh), Алексею Рипинену (Perforator), Михаилу Левшунову (Levshunovma), Михаилу Пикляеву (awoo), Алексею Слуцкому (pyloolex), Ивану Андросову (BledDest), Олегу Смирнову (Oleg_Smirnov) И Роману Кирееву (RoKi) за прорешивание задач и написание разборов.
Участникам будет предложено семь задач и два с половиной часа на их решение. Разбалловка 500-1000-1500-2000-2500-3000-3000.
UPD Разбор
UPD2 Поздравляем победителей!
Привет, Codeforces!
3 октября 2016 года в 14:35 MSK состоится очередной раунд Codeforces #375 для участников из второго дивизиона. Традиционно, участники из первого дивизиона приглашаются поучаствовать в соревновании вне конкурса. Обратите внимание на необычное время начала раунда!
Этот раунд проводится по задачам школьного этапа Всероссийской олимпиады школьников по информатике 2016/2017 года г. Саратова. Задачи для вас готовил я и Михаил Мирзаянов (MikeMirzayanov).
Хотелось бы сказать большое спасибо Глебу Евстропову (GlebsHP) за помощь в подготовке задач, а также идею самой сложной задачи, сделанной специально для раунда, Татьяне Семёновой (Tatiana_S) за перевод условий на английский, а также Николаю Калинину (KAN) за прорешивание задач и дельные советы.
Участникам будет предложено шесть задач и два с половиной часа на их решение.
Разбалловка 500-1000-1500-2000-2500-3000. Всем удачи!
UPD Если вы школьник из Саратова и писали сегодня школьный этап Всероссийской олимпиады по информатике, убедительная просьба не принимать участие в сегодняшнем соревновании!
UPD2 Разбор
Скоро...
Привет, Codeforces!
29 июля 2016 года в 18:00 MSK состоится пятнадцатый учебный раунд Educational Codeforces Round 15 для участников из первого и второго дивизионов.
О формате и деталях проведения учебных раундов более подробно вы можете прочитать здесь.
Раунд будет нерейтинговым. Соревнование будет проводиться по немного расширенным правилам ACM ICPC. На решение задач у вас будет два часа. После окончания раунда будет период времени длительностью в один день, в течение которого вы можете попробовать взломать абсолютно любое решение (в том числе свое). Причем исходный код будет предоставлен не только для чтения, но и для копирования. Таким образом вы можете локально тестировать решение, которое хотите взломать, или, например, запустить стресс-тест.
Так как Эдвард Edvard Давтян сильно занят на своей новой работе, мы с Михаилом MikeMirzayanov Мирзаяновым решили подготовить для вас этот раунд. Вам будет предложено шесть задач и два часа на их решение.
Good luck and have fun!
UPD Соревнование завершено, всем спасибо! Разбор
Привет, Codeforces!
25 мая 2016 года в 18:05 MSK (время московское) состоится очередной раунд Codeforces #354 для участников из второго дивизиона. Традиционно, участники из первого дивизиона приглашаются поучаствовать в соревновании вне конкурса. Как обычно, обратите внимание на необычное время начала раунда.
В этот раз задачи для вас готовили я и Григорий AGrigorii Ахременко (это его дебют в качестве автора задач).
Хотелось бы сказать большое спасибо Глебу GlebsHP Евстропову за помощь в подготовке задач, Михаилу MikeMirzayanov Мирзаянову за замечательные системы Codeforces и Polygon, а также Илье IlyaLos Лось (да, его фамилия не склоняется!) и Артуру ikar Свечникову за прорешивание задач и ценные советы.
Участникам будет предложено пять задач и два часа на их решение. Разбалловка будет объявлена позднее.
UPD Разбалловка 500-1000-1500-2250-2250
UPD2 Разбор
UPD3 Поздравляем победителей
UPD4 До скорых новых встреч!=)
670A - Holidays
Данная задача может быть решена несколькими способами. Рассмотрим один из них. Реализуем функцию, которая по стартовому дню года определяет количество выходных в нём. Для этого просто переберем все дни в году начиная с первого и будем проверять текущий день — выходной это день или нет. Несложно понять, что если первый день недели совпадает с началом года, то в этом году будет минимальное количество выходных. Если же начало года совпадает с первым выходным в неделе (в нашем понимании это суббота), то в этом году будет максимальное количество выходных дней.
670B - Game of Robots
Для решения данной задачи будем перебирать сколько идентификаторов назовут роботы в порядке слева направо. Договоримся, что будем решать эту задачу в 1-индексации. Пусть текущий робот назовёт i идентификаторов, тогда если k - i > 0 выполним k = k - i и перейдем к следующему роботу, в противном случае, выведем a[k], где a — это массив с идентификаторами роботов, и закончим алгоритм.
670C - Cinema
Воспользуемся map-ом (назовём его cnt) и насчитаем, сколько учёных говорит на каждом языке (то есть cnt[i] должно быть равно количеству учёных, которые говорят на языке номер i). Заведём пару res, в которой будем хранить количество \textit{очень довольных} учёных и количество \textit{почти довольных} учёных. Изначально выполним присвоение res = make_pair(0, 0). Переберем все фильмы, начиная с первого. Пусть текущий фильм имеет номер i. Тогда, если res < make_pair(cnt[b[i]], cnt[a[i]]), выполним присвоение res = make_pair(cnt[b[i]], cnt[c[i]]) и обновим ответ номером текущего фильма.
670D1 - Magic Powder - 1
Данную задачу с уменьшенными ограничениями можно решить следующим образом. Будем печь по одной печеньке до тех пор пока это возможно. Для каждой новой печеньки насчитаем val — сколько нужно волшебного порошка для её приготовления. Для этого переберём все ингредиенты, и для ингредиента номер i, если a[i] ≤ b[i] выполним присвоение b[i] = b[i] - a[i], в противном случае, выполним присвоение b[i] = 0 и val = val + a[i] - b[i]. После того, как мы перебрали все ингредиенты, если val > k, то больше печенек испечь мы не сможем. В противном случае, выполним присвоение k = k - val и перейдем к приготовлению следующей печеньки.
670D2 - Magic Powder - 2
Будем делать бинарный поиск по ответу. Пусть мы проверяем текущий ответ cur. Тогда целевая функция должна выглядеть следующим образом. Насчитаем в переменную cnt сколько грамм волшебного порошка нам нужно для приготовления cur печенек. Переберём все ингредиенты по очереди. Пусть текущий ингредиент имеет номер i. Тогда если a[i]·cur > b[i] выполним присвоение cnt = cnt + a[i]·cur - b[i]. Если после рассмотрения какого-то ингредиента cnt стало больше чем k, целевая функция должна вернуть false. Если такого не произошло ни после какого ингредиента, целевая функция должна вернуть true.
Понятно, что если целевая функция вернула true нужно сдвинуть левую границу бинпоиска в cur, иначе нужно сдвинуть правую границу.
670E - Correct Bracket Sequence Editor
Будем решать данную задачу следующим образом. Сначала с помощью stack насчитаем массив pos, где pos[i] будет означать позицию скобки, парной для скобки в позиции i. Затем заведём два массива left и right. Тогда left[i] будет равно позиции ближайшей слева относительно позиции i неудалённой скобки, а right[i] будет равно позиции ближайшей справа относительно позиции i неудалённой скобки. Если таковых скобок нет, будет хранить в соответствующей позиции в массиве число \texttt{-1}.
Пусть текущая позиция курсора равна p. Тогда при операции \texttt{L} выполним присвоение p = left[p], а при операции \texttt{R} выполним присвоение p = right[p]. Осталось научиться обрабатывать операцию \texttt{D}.
Пусть lf равно p, а rg равно pos[p]. Если lf > rg сделаем swap(lf, rg). То есть теперь мы знаем границы подстроки, которую нужно удалить. Пересчитаем сначала позицию p. Если right[rg] = = - 1 (то есть после удаления текущей подстроки не останется скобок справа), нужно сдвинуть p влево, то есть выполнить присвоение p = left[lf], иначе нужно выполнить присвоение p = right[rg]. Осталось только пересчитать ссылки для концов удаляемой подстроки. Здесь нужно быть аккуратным, и проверять есть ли скобки слева и справа относительно концов удаляемой подстроки.
Для вывода ответа нужно определить номер первой слева неудалённой скобки, с помощью массива right пройти по всем неудалённым скобкам и вывести их в ответ. Для определения номера первой неудалённой скобки можно сложить все пары концов удаляемых подстрок в массив, затем отсортировать его и, проитерировавшись по полученному массиву, определить искомую позицию. Бонус: как определить позицию первой неудалённой скобки за линейное время?
670F - Restore a Number
Сначала нужно найти длину изначального числа. Для этого просто переберем её. Пусть текущая длина равна len. Тогда если len равно длине заданной строки минус количество цифр в числе len, то len это и есть длина изначального числа (то есть она определяется однозначно). Затем нужно убрать из заданной строки все цифры, которые есть в числе len, сгенерировать три строки из оставшихся цифр и выбрать из них лексикографически минимальную — это и будет ответом. Пусть t — это подстрока, которую запомнил Вася. Какие же три строки нужно сгенерировать?
Записать сначала строку t, а затем все оставшиеся цифры из заданной строки в возрастающем порядке. Эта строка может быть составлена, только если t не начинается с нуля.
Записать сначала наименьшую цифру из оставшихся в заданной строке отличную от нуля в начало. Если таковой нет, то такую строку составить мы не сможем. В противном случае, нужно записать все оставшиеся цифры, меньшие первой цифры в строке t в возрастающем порядке, затем дописать строку t и затем все оставшиеся цифры в возрастающем порядке.
Записать сначала наименьшую цифру из оставшихся в заданной строке отличную от нуля в начало. Если таковой нет, то такую строку составить мы не сможем. В противном случае, нужно записать все оставшиеся цифры, меньшие или равные первой цифре в строке t в возрастающем порядке, затем дописать строку t и затем все оставшиеся цифры в возрастающем порядке.
Также нужно отдельно рассмотреть случай, когда число, которое передавал Вася, равно нулю.
Лучше поздно, чем никогда...
644A - Parliament of Berland
Из условия задачи следует, что либо демократов и республиканцев поровну (если n чётно), либо демократов на одного больше (если n нечётно). Так как представители одной и той же партии не должны сидеть на соседних креслах, представим парламентский зал в виде шахматной доски, где левая верхняя клетка будет белой. Затем начнем перебирать ряды клеток сверху вниз, а клетки в каждом ряду слева направо и будем по очереди сажать парламентариев — демократов в белые клетки, а республиканцев в черные.
Таким образом, если n > a·b, ответом будет - 1. В противном случае рассадка всегда найдется.
Для определения того, какого цвета клетка (и, соответственно, кого нужно в нее посадить), находящаяся в i-й строке и j-м столбце (в случае, если они нумеруются с единицы), можно поступить следующим образом. Если (i + j)mod2 = 0, значит соответствующая клетка должна быть белой, иначе чёрной.
Основная часть решения:
cin >> n >> a >> b;
m = n - 1;
if (n > a * b) {
cout << -1;
return 0;
}
for (int i = 0; i < a; i++) {
for (int j = 0; j < b; j++) {
if ((i + j) % 2 == 0) {
cout << n << " ";
n = max(n - 2, 0);
} else {
cout << m << " ";
m = max(m - 2, 0);
}
}
cout << endl;
}
644B - Processing Queries
Для решения данной задачи очень удобно воспользоваться структурой данных, которая называется очередь.
Очередь — это структура данных со следующим принципом доступа к элементам: «первый пришёл — первый ушёл». Добавление элемента (\textit{push}) возможно лишь в конец очереди, а взять элемент из очереди можно только из её начала (\textit{front}). Удалить элемент можно также только из начала очереди (\textit{pop}).
В данной задаче нужно было перебрать все запросы в хронологическом порядке. Будем хранить в очереди времена окончания обработки запросов. Для текущего запроса, пока в начале очереди находятся запросы, которые закончат обрабатываться не позднее, чем появился текущий запрос, нужно просто удалять их из начала очереди, так как они никак не повлияют на текущий. Если после этих действий размер очереди равен максимальному допустимому числу, ответ для текущего запроса - 1. В противном случае, нужно добавить время окончания обработки текущего запроса в очередь, вывести это время и продолжить алгоритм.
Основная часть решения:
queue<long long> q;
int main() {
cin >> n >> b;
for (int i = 0; i < n; i++) {
cin >> t >> d;
while (q.size() && q.front() <= t)
q.pop();
if (q.empty())
ans = t;
if (q.size() <= b) {
ans += d;
q.push(ans);
cout << ans << ' ';
} else
cout << -1 << ' ';
}
}
644C - Hostname Aliases
Для решения данной задачи воспользуемся структурами данных map и set. Переберем все имеющиеся адреса страниц, затем получим hostname и path для каждого адреса, и добавим текущий path в множество путей для текущего hostname (для этого будет нужен map, где ключом будет строка hostname, а значением — множество строк path).
Осталось только объединить все hostname, множества путей которых совпадают (это можно сделать с помощью map, где ключом будет множество строк path, а значением — вектор строк hostname), и вывести те группы, размер которых больше единицы.
Основная часть решения:
cin >> n;
for (int i = 0; i < n; i++) {
cin>>s, s += '/';
int p = s.find('/',7);
m[s.substr(0, p)].insert(s.substr(p));
}
for (auto &i:m) {
v[i.second].push_back(i.first);
k += (v[i.second].size() == 2);
}
cout<< k << endl;
for (auto &i:v) {
if (i.second.size()>1) {
for (auto &j:i.second) cout << j << ' ';
cout << endl;
}
}
649A - Любимые числа Поликарпа
Для решения данной задачи нужно воспользоваться фактом, что степени двойки быстро растут, и максимальная степень двойки, на которую может делится число, не превосходящее 109, равна 29. Поэтому нужно просто проитерироваться по заданным числам, найти максимальную степень двойки, на которую делится текущее число и обновить ответ этой максимальной степенью.
Основная часть решения:
int n, x;
int main() {
cin >> n;
int ans = -1, cnt = 0;
for (int i = 0; i < n; i++) {
cin >> x;
int cur = 1, power = 0;
while (true) {
cur *= 2;
if (x % cur) break;
power++;
}
if (ans < power) {
ans = power;
cnt = 1;
} else if (ans == power) {
cnt++;
}
}
cout << ans << ' ' << cnt << endl;
}
649B - Этажи
Для решения данной задачи нужно было аккуратно реализовать то, что написано в условии. Основная сложность заключалась в определении номера подъезда и номера этажа по номеру квартиры. Это можно было сделать следующим образом: если в доме n подъездов, в каждом подъезде по m этажей, а на каждом этаже по k квартир, то квартира с номером a находится в подъезде номер (a - 1) / (m * k) и на этаже номер ((a - 1)%(m * k)) / k, причем эти номера 0-индексированы, что удобно для дальнейших вычислений. После определения номеров подъездов и этажей, нужно было рассмотреть два случая — когда номера подъездов Эдварда и Наташи равны (тогда нужно было выбрать, что оптимальнее — доехать на лифте или подняться/спуститься по лестнице), и когда эти номера различны (тут нужно было не забыть, что дом круглый, и выбрать нужное направление).
Основная часть решения:
int n, m, k, a, b;
int main() {
cin >> n >> m >> k >> a >> b;
a--, b--;
int p1 = a / (m * k), p2 = b / (m * k);
int f1 = (a % (m * k)) / k, f2 = (b % (m * k)) / k;
if (p1 == p2) {
cout << min(abs(f1 - f2) + 10, abs(f1 - f2) * 5) << endl;
} else {
if(p1 > p2) swap(p1, p2);
cout << min((p2 - p1) * 15, (p1 + n - p2) * 15) + min(f1 * 5, 10 + f1) + min(f2 * 5, 10 + f2) << endl;
}
}
649C - Печать условий
Сначала отсортируем заданные размеры комплектов задач в неубывающем порядке. Затем нужно начать перебирать комплекты задач, начиная с наименьшего. Если мы не можем напечатать текущий комплект, то никакой следующий комплект мы гарантированно не сможем напечатать, поэтому нужно вывести ответ и закончить алгоритм. В противном случае нужно напечатать текущий комплект, увеличить ответ на единицу и перейти к следующему комплекту. Каждый комплект оптимально печатать следующим образом. Пусть x — это оставшееся количество двусторонних листов, y — это оставшееся количество односторонних листов, а a — это количество страниц в текущем комплекте задач. Если x = 0 и y = 0, то напечатать текущий комплект мы точно не сможем. Если a нечетно и y > 0, напечатаем одну страницу на одностороннем листе и уменьшим a и y на единицу, иначе если a нечетно и x > 0, напечатаем одну страницу на двустороннем листе (который больше использовать не будем) и уменьшим a и x на единицу. Теперь a это всегда четное число. Поэтому выгодно сначала по максимуму использовать для печати двусторонние листы, а если их не хватает — односторонние. Если и односторонних листов не хватает, то текущий комплект распечатать мы не сможем.
Основная часть решения:
int n, x, y;
int a[N];
bool can(int a)
{
if (a % 2) {
if (y > 0) a--, y--;
else if (x > 0) a--, x--;
else return false;
}
if (x * 2 >= a) {
x -= a / 2;
return true;
}
a -= 2 * x, x = 0;
if (y >= a) {
y -= a;
return true;
}
return false;
}
int main() {
cin >> n >> x >> y;
for (int i = 0; i < n; i++) cin >> a[i];
sort(a, a + n);
int ans = 0;
for (int i = 0; i < n; i++)
if(can(a[i])) ans++;
else break;
cout << ans << endl;
}
649D - Дефрагментация памяти
Для решения данной задачи нужно сформировать массив, который будет равен памяти компьютера после дефрагментации. Для этого, например, можно запомнить про каждый процесс (в порядке слева направо) количество ячеек, которые он занимает. Верно следующее утверждение — пока дефрагментация не закончена, всегда будет две такие ячейки с номерами pos1 и pos2 в памяти компьютера, что ячейка pos1 пуста, а ячейка pos2 занята процессом, который по окончании дефрагментации должен находится в ячейке номер pos1. Таким образом, ответ на задачу, это количество таких ячеек в памяти, которые должны быть заняты каким-то процессом после окончания дефрагментации, причем до начала дефрагментации эти ячейки либо пусты, либо в них записаны другие процессы (отличные от тех, которые должны быть записаны после дефрагментации).
Основная часть решения:
int n;
int a[N], need[N];
int szneed;
int main() {
cin >> n;
for (int i = 0; i < n; i++) {
cin >> a[i];
if (a[i] != 0) need[szneed++] = a[i];
}
int ans = 0;
for (int i = 0; i < n; i++) {
if (need[i] != 0 && need[i] != a[i]) ans++;
}
cout << ans << endl;
}
649E - Автобус
Изначально отсортируем всех путешественников по их начальным позициям в неубывающем порядке, а при равенстве позиций — отсортируем по дистанциям, которые путешественникам нужно преодолеть, также в неубывающем порядке. Затем необходимо бинарным поиском подобрать минимальное количество мест в автобусе, которых будет достаточно для перевозки a путешественников.
Целевая функция бинарного поиска должна работать следующим образом. Пусть mid — количество мест в автобусе. Тогда найдем cnt — максимальное количество путешественников, которых мы сможем подвезти на таком автобусе. Это можно сделать с помощью set-a, в котором мы будем хранить позиции выходов путешественников, которые зашли в автобус, и их индексы.
Переберем всех путешественников слева направо (в том порядке, в котором они были отсортированы). Пока в set-е есть путешественники, которые выйдут из автобуса не позднее момента, когда зайдет текущий путешественник, удалим позиции их выходов из set и добавим их индексы в отдельный вектор ans. В противном случае, если самая дальняя позиция выхода путешественника в set-е больше, чем потенциальная позиция выхода текущего путешественника, заменим в set-е самого дальневыходящего путешественника на текущего.
После того, как мы переберем всех путешественников, добавим индексы всех оставшихся в set-е путешественников в ans. Если размер вектора ans меньше a, сдвинем в mid левую границу бинарного поиска, иначе сдвинем в mid правую границу бинарного поиска. После бинарного поиска, запустим еще раз целевую функцию от ответа и выведем индексы путешественников из вектора ans.
Основная часть решения:
int n, a;
vector<pair<pair<int, int>, int > > v;
set<pair<int, int> > s;
vector<int> ans;
int ok (int x) {
s.clear();
ans.clear();
for (int i = 0; i < n; i++) {
int l = v[i].first.first, r = v[i].first.second;
while (!s.empty() && s.begin()->first <= l) {
ans.push_back(s.begin()->second);
s.erase(s.begin());
}
if ((int)s.size() + 1 <= x) s.insert(mp(r, v[i].second));
else {
s.insert(make_pair(r, v[i].second));
set<pair<int, int> > :: iterator it = s.end();--it;
s.erase(it);
}
}
while (!s.empty()) {
ans.push_back(s.begin()->second);
s.erase(s.begin());
}
return (int)ans.size();
}
int main() {
cin >> n >> a;
v.resize(n);
for (int i = 0; i < n; i++)
cin >> v[i].first.first >> v[i].first.second, v[i].first.second += v[i].first.first, v[i].second = i;
sort(v.begin(), v.end());
int l = 0, r = a;
while (r - l > 1) {
int mid = (l + r) / 2;
if(ok(mid) >= a)
r = mid;
else
l = mid;
}
ok(r);
cout << r << endl;
for (int i = 0; i < a; i++)
cout << ans[i] + 1 << ' ';
cout << endl;
}
648A - Наибольший подъем
Для решения данной задачи насчитаем высоту каждой горы и сохраним ее в массиве h[], где h[j] равно высоте j-й горы. Для этого обойдем заданную матрицу, и если элемент, стоящий в строке i и в столбце j (строки и столбцы 0-индексированы), равен звездочке, обновим высоту j-й горы: h[j] = max(h[j], n - i). Осталось просто проитерироваться по столбцам от 0 до m — 2 включительно, и, если текущий столбец равен j, обновить величину максимального подъема или максимального спуска величиной |h[j + 1] - h[j]|.
Основная часть решения:
int n, m;
int h[N];
char c;
void solve() {
cin >> n >> m;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> c;
if (c == '*') {
h[j] = max(h[j], n - i);
}
}
}
int maxU = 0, maxD = 0;
for (int i = 0; i < m - 1; i++) {
int diff = h[i + 1] - h[i];
if (diff > 0) {
maxU = max(maxU, diff);
} else {
maxD = max(maxD, -diff);
}
}
cout << maxU << ' ' << maxD << endl;
}
648B - Собери стол
Для решения данной задачи сначала посчитаем длину одной собранной ножки стола и сохраним ее в переменную len (len = sum / n, где sum — это суммарная длина всех частей, а n — количество ножек стола). Сохраним длины всех частей ножек в массив a[] и отсортируем его по возрастанию. Затем переберем части ножек переменной i от 0 до n - 1 включительно и будем выводить в ответ пары вида (a[i], len - a[i]).
Основная часть решения:
int n, len, sum;
int a[N];
int main() {
cin >> n;
for (int i = 0; i < 2 * n; i++) {
cin >> a[i];
sum += a[i];
}
len = sum / n;
sort(a, a + 2 * n);
for (int i = 0; i < n; i++) {
cout << a[i] << ' ' << len - a[i] << endl;
}
}
648C - Путь Робота
Сначала найдем стартовую позицию Робота, сохраним ее и присвоим значение стартовой позиции звездоке. Так как по условию задана ломаная без самопересечений и самокасаний верен следующий алгоритм: если есть соседняя с текущей клетка, в которой стоит звездочка, перейдем в соседнюю клетку, значение которой равно звездочке, и присвоим ее значение точке (при этом выведем букву, соответствующую направлению, в котором мы перешли). При этом соседняя клетка должна быть отлична от той, из которой мы пришли в текущую клетку. Если нет соседней клетки с звездочкой, значит мы обошли всю ломаную и нужно закончить работу программы.
Основная часть решения:
int n, m, sx, sy;
char a[N][N];
int dx[] = {-1, 1, 0, 0};
int dy[] = {0, 0, -1, 1};
char dir[] = {'U', 'D', 'L', 'R'};
void solve()
{
cin >> n >> m;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++)
{
cin >> a[i][j];
if (a[i][j] == 'S') {
sx = i, sy = j;
}
}
}
a[sx][sy] = '*';
int px = -1, py = -1;
while (true) {
bool wasMove = false;
for (int i = 0; i < 4; i++) {
int nx = sx + dx[i];
int ny = sy + dy[i];
if (nx < 0 || nx >= n || ny < 0 || ny >= m) {
continue;
}
if (a[nx][ny] != '*') {
continue;
}
if (nx == px && ny == py) {
continue;
}
a[nx][ny] = '.';
px = sx, py = sy;
sx = nx, sy = ny;
cout << dir[i];
wasMove = true;
break;
}
if(wasMove) {
break;
}
}
puts("");
}
648D - Собачки и миски
Если представить каждую миску в виде отрезка [uj - tj, uj + tj], то i-я собачка сможет покушать из j миски, если uj - tj ≤ xi ≤ uj + tj.
Будем решать задачу жадно. Рассмотрим самую левую собачку и те миски из которых она может покушать. Если таких мисок нет, то собачка не сможет покушать. В противном случае из мисок доступных самой левой собачке выберем для неё миску с самым левым правым концом. Далее не будем рассматривать эту собачку и эту миску и продолжим аналогично наши рассуждения.
Легко видеть, что такая жадность приводит к оптимальному ответу:
- Если самая левая собачка может покушать, то нет смысла ей не кушать, поскольку этим мы убираем одну миску и ухудшим ответ на единицу;
- Рассмотрим те миски из которых может покушать самая левая собачка. Все эти миски будут доступны и остальным собачкам кроме тех у которых правая граница находится слишком далеко влево. Таким образом, если мы хотим взять какую-либо миску (а мы уже поняли из пункта 1, что это стоит сделать), то выгоднее будет взять миску с самым левым правым концом, так мы не ухудшим выбор для собачек справа.
По этой задаче можно было попробовать написать другие жадности, но многие являются неправильными.
Для того, чтобы это реализовать отсортируем собачек и миски (по левому концу) слева направо. Будем идти слева-направо обрабатывая события появилась миска (в этом случае добавим её правый конец в какую-нибудь структуру данных) и появилась собачка (нужно для собачки в структуре данных найти самый левый подходящий правый конец).
Сложность: O(nlogn) или O(n) в зависимости от структуры данных (*set* или queue).
const int N = 200200;
int n, m;
int x[N];
int u[N], t[N];
bool read() {
if (!(cin >> n >> m)) return false;
forn(i, n) assert(scanf("%d", &x[i]) == 1);
forn(i, m) assert(scanf("%d%d", &u[i], &t[i]) == 2);
return true;
}
pti segs[N];
void solve() {
forn(i, m) segs[i] = mp(u[i] - t[i], u[i] + t[i]);
sort(x, x + n);
sort(segs, segs + m);
int ans = 0;
multiset<int> z;
for (int i = 0, j = 0; i < n; ) {
if (j < m && segs[j].x <= x[i]) {
z.insert(segs[j].y);
j++;
} else {
auto it = z.lower_bound(x[i]);
i++;
if (it != z.end()) {
ans++;
z.erase(it);
}
}
}
cout << ans << endl;
}
648E - Собери число
Заметим, что при построении ответа нам в любой момент важен только лишь остаток от деления текущего его префикса на k. Действительно, если текущий префикс ответа имеет остаток от деления на k, равный r, то при приписывании к префиксу числа ai этот остаток станет равный остатку от деления на k числа r·10li + ai (li — количество цифр в записи числа ai).
Тогда, очевидно, нас интересует получать любой остаток от деления такой операцией, используя минимальное количество цифр в записи. Конечно, остаток 0 мы можем получить сразу, используя пустой префикс, поэтому для остатка 0 нас будет интересовать второй по величине ответ.
Все описанное выше позволяет нам построить граф на k вершинах (от 0 до k - 1, соответственно остаткам), ребра в котором определяются числами ai: из вершины v в вершину 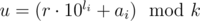 длины li, означающее, что с помощью дописывания li цифр мы можем из префикса с остатком v получить префикс с остатком u. Легко заметить, что некоторые ai в этом графе будут соответствовать одним и тем же ребрам (сейчас их nk) — это числа с одинаковой длиной десятичной записи и остатком от деления на k, поэтому стоит оставить лишь уникальные по такому критерию числа (их будет не больше 10k), и тогда количество ребер не будет превышать 10k2.
длины li, означающее, что с помощью дописывания li цифр мы можем из префикса с остатком v получить префикс с остатком u. Легко заметить, что некоторые ai в этом графе будут соответствовать одним и тем же ребрам (сейчас их nk) — это числа с одинаковой длиной десятичной записи и остатком от деления на k, поэтому стоит оставить лишь уникальные по такому критерию числа (их будет не больше 10k), и тогда количество ребер не будет превышать 10k2.
Теперь все, что от нас требуется — найти длину кратчайшего непустого пути из вершины 0 в саму себя же в построенном графе. Чтобы избежать столь неприятной цикличности, давайте просто добавим дополнительную вершину k, имеющую те же исходящие ребра, что и вершина 0, считая, что такой остаток может иметь лишь пустой префикс. Теперь задача сводится к нахождению кратчайшего пути из вершины k в вершину 0, которую можно решить алгоритмом Дейкстры за O(k2). Однако, в силу специфичности задачи, решение алгоритмом Форда-Беллмана (с правильными отсечениями, конечно) так же проходит все тесты, хоть в теории и имеет столь большие O(k3).
Восстановление ответа в задаче довольно стандартно, за исключением хранения дополнительного числа для каждой вершины, образовавшего ребро, по которому был осуществлен нужный в кратчайшем ответе переход.
Основная часть:
for (int i = 0; i < n; ++i) {
int x;
assert(scanf("%d", &x) == 1);
any[x % k][length(x)] = x;
}
p10[0] = 1;
for (int i = 0; i + 1 < P; ++i)
p10[i + 1] = (p10[i] * 10) % k;
for (int i = 0; i <= k; ++i) {
d[i] = int(1e9);
p[i] = -1;
used[i] = false;
}
d[k] = 0;
while (true) {
int v = -1;
for (int i = 0; i <= k; ++i)
if (!used[i] && (v == -1 || d[v] > d[i]))
v = i;
if (v == -1)
break;
if (v == 0)
break;
used[v] = true;
for (int r = 0; r < k; ++r)
for (int l = 0; l < P; ++l)
if (any[r][l] != -1) {
int to = (v * p10[l] + r) % k;
if (d[to] > d[v] + l) {
d[to] = d[v] + l;
p[to] = v;
w[to] = any[r][l];
used[to] = false;
}
}
}
if (p[0] == -1) {
puts("NO");
} else {
puts("YES");
vector <int> res;
int v = 0;
do {
res.push_back(w[v]);
v = p[v];
} while (v != k);
reverse(res.begin(), res.end());
for (auto x: res)
printf("%d", x);
}
Для начала отсечем случай, когда n нечетно. Так как периметр прямоугольника всегда четный, то ответ в таком случае 0.
Если n четно, то количество прямоугольников, которые можно составить, равно n / 4. Если n кратно 4, то мы посчитаем и квадрат, который составлять нельзя, поэтому в таком случае из ответа нужно вычесть единицу.
Асимптотика решения — O(1).
Для начала найдем минимум в заданном массиве, обозначим его переменной minimum. Понятно, что всегда возможно покрасить n * minimum клеток. Тогда понятно, что нужно найти такой минимум в массиве, перед которым слева стоит как можно больше чисел, больших чем минимум. Другими словами, нужно найти два минимума, расстояние между которыми наибольшее, с учетом цикличности. Если же минимум в массиве один, то понятно, что начинать красить нужно с цвета, который находится сразу после него (опять же с учетом цикличности). Это можно сделать за один проход по массиву, поддерживая в отдельной переменной позицию ближайшего слева минимума. Если текущее число равно минимуму, тогда нужно обновить эту переменную и ответ.
Асимптотика решения — O(n), где n — количество различных цветов.
Давайте строить ответ рекурсивно. При k = 0 в качестве ответа можно взять либо - 1 или + 1. Пусть теперь мы строим ответ для некоторого k > 0. Сначала построим ответ для k - 1 теперь как ответ для k возьмем четыре копии ответа для k - 1, инвертировав все значения в последней копии. Получается на самом деле некоторый фрактал с базой размера 2 × 2: 00, 01. Корректность доказать достаточно просто, если оба вектора из верхней (нижней) половины их левые половины дают скалярное произведение равное 0 и правые тоже дают 0. Если же один из векторов из верхней половины, а другой из нижней, то значение в левой половине будет противоположно значению в правой, поэтому сумма будет равна 0.
Можно заметить, что на самом деле ответом также является матрица в которой клетка i, j равна \texttt{+}, если количество единичных битов в числе i|j четно.
Асимптотическая сложность: O((2k)2).
Давайте сначала объединим все отрезки, находящиеся в одной горизонтали или вертикали. Теперь ответ на задачу есть сумма длин всех отрезков минус количество пересечений. Посчитаем количество пересечений. Для этого будем идти горизонтальной сканирующей прямой снизу вверх (это можно делать событиями открылся вертикальный отрезок, закрылся вертикальный и обработать горизонтальный) и в некоторой структуре данных поддерживать множество x-координат открытых отрезков. В качестве структуры данных можно использовать дерево Фенвика с предварительным сжатием координат. Теперь для текущего горизонтального отрезка нужно просто взять количество открытых вертикальных отрезков со значениями x в отрезке x1, x2, где x — вертикаль на которой находится вертикальный отрезок, а x1, x2 — x-координаты концов текущего горизонтального отрезка.
Асимптотическая сложность: O(nlogn).
Рассмотрим медленное решение этой задачи: на первый запрос будем просто переприсваивать символы, на запросы второго типа будем идти по строке s и поддерживать указатель на текущую позицию в перестановке алфавита. Будем двигать указатель по циклу пока не найдем совпадение с текущим символом в s. После этого подвинем указатель еще раз. Тогда ответом на задачу будет количество циклических переходов (от последнего к первому символу) в перестановке алфавита. На самом деле это значение равно единице плюс количество пар соседних символов таких, что второй символ находится не правее первого. Таким образом, ответ на задачу зависит лишь от значений cntij —- количество пар соседних символов таких, что первый символ ест i, а второй j. Теперь, чтобы ускорить решение будем поддерживать дерево отрезков в вершине, которого находится матрица cnt для текущего подотрезка и символы с левого и правого концов текущего отрезка. Чтобы слить двух сыновей в дереве отрезков нужно просто попарно сложить значения матриц в левом и правом сыне, и обновить значением правого символа левого отрезка с левым символов правого отрезка.
Асимптотическая сложность: O(nk2 + mk2logn).
Привет, Codeforces!
27 декабря 2015 года в 14:05 MSK (время московское) состоится очередной раунд Codeforces #337 для участников из второго дивизиона. Традиционно, участники из первого дивизиона приглашаются поучаствовать в соревновании вне конкурса. Обратите внимание на необычное время начала раунда!!!
В этот раз задачи для вас готовили я и Эдвард Давтян (Edvard).
Хотелось бы сказать большое спасибо Глебу Евстропову (GlebsHP) за помощь в подготовке задач, Марии Беловой (Delinur) за перевод условий на английский и Михаилу Мирзаянову (MikeMirzayanov) за замечательные системы Codeforces и Polygon.
Участникам будет предложено пять задач и два часа на их решение. Разбалловка будет объявлена позднее.
UPD Раунд переносится на 10 минут. Разбалловка 500-1000-1500-2500-2500
UPD2 Соревнование завершено! Всем спасибо! Разбор
Простая задача на реализацию. Проитерируемся по i от 1 до n, а внутри проитерируемся по j от 1 до 2·m, причем на каждой итерации будем увеличивать j на два. Если на текущей итерации a[i][j] = '1' или a[i][j + 1] = '1' увеличим ответ на один.
Асимптотика решения — O(nm).
Будем считать ответ для каждого блока отдельно и умножать ответ для предыдущих блоков на ответ для текущего блока, при этом не забывая брать результат перемножения по модулю.
Для блока длины k ответ считается следующим образом. Пусть для этого блока число должно делиться на x и не должно начинаться с цифры y. Тогда ответ для этого блока — количество чисел из k цифр, делящихся на x, минус количество чисел, начинающихся с цифры y и состоящих из k цифр, плюс количество чисел, начинающихся с цифры y - 1 (только если y > 0) и состоящих из k цифр.
Асимптотика решения — O(n / k).
Отсортируем все точки по возрастанию координаты x, далее будем работать с перенумерованными точками.
Предположим, что при оптимальной игре после ходов игроков остались точки с номерами l и r (l < r). Утверждается, что первый игрок не запретил ни одну из точек с индексом l < i < r, ведь в противном случае он играл не оптимально и мог запретить точку l или точку r (можно показать, что это не зависит от оптимальных действий второго игрока), поменяв оптимальный ответ. Получается, что номера всех 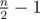 запрещенных первым игроком точек лежат вне отрезка [l, r], а значит
запрещенных первым игроком точек лежат вне отрезка [l, r], а значит 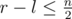 . Заметим, что выбрав некоторую такую границу [l, r] при
. Заметим, что выбрав некоторую такую границу [l, r] при 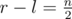 , первый игрок может всегда добиться того, чтобы точки в ответе лежали внутри этого отрезка.
, первый игрок может всегда добиться того, чтобы точки в ответе лежали внутри этого отрезка.
Второй игрок хочет добиться того, чтобы 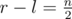 (меньше он сделать не может), то есть всегда запрещать точку, лежащую строго внутри [l, r]. Поскольку второй игрок не знает наперед, к каким точкам стремится игрок, после каждого хода первого игрока ему необходимо запрещать точку, которая лежит строго внутри каждой из возможных границ, образованных этими точками. Нетрудно показать, что эта точка является медианой оставшегося множества точек (а их нечетное количество), ведь количество оставшихся ходов первого игрока на единицу меньше количества ходов второго, и он сможет впоследствии запретить все, кроме трех медианных точек. Две крайние из них второму игроку запрещать нельзя, так как они могут впоследствии увеличить количество удаленных слева (или справа) первым игроком точек, а средняя из них как раз принадлежит всевозможным границам, которые мог выбрать первый игрок. Таким образом второй игрок всегда может свести ситуацию к
(меньше он сделать не может), то есть всегда запрещать точку, лежащую строго внутри [l, r]. Поскольку второй игрок не знает наперед, к каким точкам стремится игрок, после каждого хода первого игрока ему необходимо запрещать точку, которая лежит строго внутри каждой из возможных границ, образованных этими точками. Нетрудно показать, что эта точка является медианой оставшегося множества точек (а их нечетное количество), ведь количество оставшихся ходов первого игрока на единицу меньше количества ходов второго, и он сможет впоследствии запретить все, кроме трех медианных точек. Две крайние из них второму игроку запрещать нельзя, так как они могут впоследствии увеличить количество удаленных слева (или справа) первым игроком точек, а средняя из них как раз принадлежит всевозможным границам, которые мог выбрать первый игрок. Таким образом второй игрок всегда может свести ситуацию к 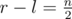 .
.
Ответ на задачу — минимум среди значений 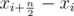 .
.
Главное утверждение для решения этой задачи — в середине дистанции каждого соревнования датчик должен находиться либо в самой верхней точке колеса, либо в самой нижней точке колеса.
Для того, чтобы посчитать ответ, воспользуемся бинпоиском. Если центр колеса прошел расстояние c то датчик переместился на расстояние c + rsin(c / r), если в середине датчик находился сверху колеса, или на расстояние c - rsin(c / r), если в середине датчие находился снизу колеса, где r — это радиус колеса.
Асимптотика решения —  .
.
Найдем центры прямоугольников и умножим их координаты на два, чтобы далее работать с целыми координатами. Тогда подходящим холодильником (для всех точек) является прямоугольник, содержащий все точки, но с длинами сторон, округленными вверх к ближайшему четному числу.
Представим теперь, что удаляем магниты с холодильника последовательно, постепенно "уменьшая" прямоугольник. Очевидно, что каждый раз выгодно удалять только те точки, что лежат на какой-то из четырех сторон прямоугольника. Переберем 4k вариантов того, как мы будем это делать, с помощью рекурсии, каждый раз удаляя одну из еще не удаленных точек с максимальным или минимальным значением по одной из координат. Если мы будем поддерживать 4 массива (или два массива в виде дека), то это можно делать за O(1) амортизированно. Такое решение будет работать за O(4k).
Можно также заметить, что описанный выше алгоритм удаляет всегда несколько самых правых, левых, верхних, и нижних точек. Можно перебрать, как k распределится среди этих величин и промоделировать удаление с помощью, например, описанных выше 4 массивов. Такое решение имеет асимптотику O(k4).
Для подсчета ответа на каждый запрос будем пользоваться формулой 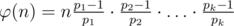 , где p1, p2, ..., pk — все простые, делящие n. Эту формулу каждый может попробовать доказать или воспользоваться уже существующими доказательствами. Все вычисления ниже производим по модулю 109 + 7
, где p1, p2, ..., pk — все простые, делящие n. Эту формулу каждый может попробовать доказать или воспользоваться уже существующими доказательствами. Все вычисления ниже производим по модулю 109 + 7
Предположим теперь, что мы решаем задачу для фиксированного левого конца отрезка l, отбросив все элементы левее. Любой запрос теперь превращается в запрос на префиксе массива. Тогда, судя по формуле, для каждого простого p нас интересует лишь его самое левое вхождение, потому что все остальные вхождения не будут влиять на правую часть в приведенной выше формуле. Превратим наш запрос на значение функции Эйлера в запрос произведения на префиксе: сначала проинициализируем дерево Фенвика произведений единицами, затем сделаем умножения в точках l, l + 1, ..., n значениями соответствующих элементов al, al + 1, ..., an, затем для каждого самого левого вхождения простого p в позицию i сделаем умножение в точке i на значение 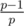 . Нетрудно убедиться, что теперь запрос на префиксе определенной длины даст правильный ответ для отрезка той же длины с левым концом в l. Такую подготовку для фиксированного левого конца можно осуществить за
. Нетрудно убедиться, что теперь запрос на префиксе определенной длины даст правильный ответ для отрезка той же длины с левым концом в l. Такую подготовку для фиксированного левого конца можно осуществить за 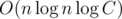 , где C — максимальное значение элемента (этот логарифм соответствует количеству простых в разложении какого-то из ai).
, где C — максимальное значение элемента (этот логарифм соответствует количеству простых в разложении какого-то из ai).
Нас интересуют все левые концы, поэтому научимся переходить от одного из них к другому. В самом деле, пусть все было посчитано для левого конца l и мы хотим теперь перейти к левому концу l + 1. Нас перестает интересовать al внутри левой части формулы, поэтому сделаем умножение в дереве Фенвика в точке l на значение al - 1. Так же нас перестают интересовать все простые внутри al (а они, очевидно, самые левые среди своих вхождений), поэтому сделаем так же умножения в точке l на все значения 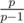 . Однако у каждого из этих простых могли существовать другие вхождения, которые теперь станут самыми левыми. Добавим их с помощью умножений, описанных выше. С помощью сортировок (или векторов) переход между соседними левыми концами реализуется за суммарную
. Однако у каждого из этих простых могли существовать другие вхождения, которые теперь станут самыми левыми. Добавим их с помощью умножений, описанных выше. С помощью сортировок (или векторов) переход между соседними левыми концами реализуется за суммарную 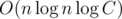 .
.
Чтобы правильно отвечать на запросы, их так же нужно правильно отсортировать (или поместить в динамический массив), и ответ на запрос будет совершать  операций. Суммарная асимптотика всего решения
операций. Суммарная асимптотика всего решения 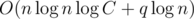 операций и
операций и 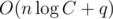 дополнительной памяти.
дополнительной памяти.
Опишем жадный алгоритм, который позволяет решить задачу при k > 2 для любой строки S.
Будем считать, что мы всегда переворачиваем некоторый префикс строки S (возможно, длины 1, подробнее ниже). Поскольку мы стремимся минимизировать строку лексикографически, легко убедиться в том, что мы будем переворачивать такие и только такие префиксы, префикс которых (после переворачивания) совпадает с минимальным лексикографически суффиксом перевернутой строки S (обозначим ее Sr), в частности, это префикс, совпадающий по длине с минимальным суффиксом Sr (операция переворачивания префикса S равносильна замене его суффиксом Sr соответствующей длины).
Обозначим минимальный лексикографически суффикс строки Sr как s. Можно показать, что никакие два вхождения s в Sr не пересекаются, так как в противном случае строка s была бы периодической, и минимальный суффикс имел бы меньшую длину. Значит, строка Sr имеет вид tpsaptp - 1sap - 1tp - 2... t1sa1, где sx означает конкатенацию строки s x раз, a1, a2, ..., ap — натуральные числа, а строки t1, t2, ..., tp — некоторые непустые (кроме, возможно, tp) строки, не содержащие s в качестве подстроки.
Перевернув некоторый подходящий префикс строки S, мы перейдем к меньшей строке S', при этом минимальный суффикс s' этой перевернутой строки S'r не может быть лексикографически меньше, чем s (это каждый может доказать самостоятельно), поэтому мы стремимся сделать так, чтобы s' осталось равным s, что позволит увеличить префикс вида sb в ответе (а значит и минимизировать его). Легко доказать, что максимальное b, которое мы можем получить, равно a1 в случае p = 1 и 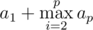 (в случае, если p \geq 2$). Действительно, после таких операций префикс ответа будет выглядеть как sa1saitisai - 1... sa2t2. Поскольку t_{i} — непустые строки, увеличить количество конкатенаций s в префиксе ответа никак не получится. Заметим, что переворот второго префикса (sai...) возможен, так как k > 2.
(в случае, если p \geq 2$). Действительно, после таких операций префикс ответа будет выглядеть как sa1saitisai - 1... sa2t2. Поскольку t_{i} — непустые строки, увеличить количество конкатенаций s в префиксе ответа никак не получится. Заметим, что переворот второго префикса (sai...) возможен, так как k > 2.
Из описанных выше утверждений следует, что при k > 2 для оставшейся строки всегда следует переворачивать префикс, который после переворота совпадает с суффиксом строки Sr вида sa1. Чтобы находить этот суффикс каждый раз, достаточно один раз построить декомпозицию Линдона (с помощью алгоритма Дюваля) перевернутой исходной строки и аккуратно объединять равные строки в ней. Единственным случаем остается вариант, когда префикс оставшейся строки переворачивать не нужно — его можно обработать как конкатенацию последовательных переворачиваемых префиксов длины 1.
Поскольку для k = 1 задача тривиальна, осталось решать задачу для k = 2, то есть деление строки на две части (префикс и суффикс) и какой-то способ их переворачивания. Случай, когда ничего не переворачивается, нам не интересен, рассмотрим два других случая:
Префикс не переворачивается. В таком случае обязательно переворачивается суффикс. Два варианта строки с перевернутым суффиксом можно сравнивать за O(1) с помощью z-функции строки Sr#S.
Префикс переворачивается. Для решения этого случая можно воспользоваться утверждениями из разбора задачи F Яндекс.Алгоритма 2015 из Раунда 2.2 авторства GlebsHP и рассмотреть только два варианта поворота префикса, перебрав для каждого из них все два варианта поворота суффикса.
Остается выбрать из двух случаев лучший ответ. Итоговая асимптотика решения O(|s|).
Привет, Codeforces!
28 сентября 2015 года в 12:00 MSK состоится очередной раунд Codeforces #322 для участников из второго дивизиона. Традиционно, участники из первого дивизиона приглашаются поучаствовать в соревновании вне конкурса. Обратите внимание на необычное время начала раунда!
Этот раунд проводится по задачам школьного этапа Всероссийской олимпиады школьников по информатике 2015/2016 года г. Саратова. Задачи для вас готовил я и недавно вернувшийся из армии Эдвард Давтян (Edvard).
Хотелось бы сказать большое спасибо Максиму Ахмедову (Zlobober) за помощь в подготовке задач, Марии Беловой (Delinur) за перевод условий на английский, Михаилу Мирзаянову (MikeMirzayanov) за замечательные системы Codeforces и Polygon, а также Владимиру Петрову (vovuh) за прорешивание задач.
Участникам будет предложено шесть задач и два часа на их решение. Разбалловка будет объявлена позднее.
UPD Разбалловка задач 500-1000-1500-2000-3000-3000. Всем удачи!
UPD2 Разбор
UPD3 Поздравляем победителей!
581A — Хипстер Вася
Первое ответное число (количество дней, которое Вася сможет быть одет по моде) это min(a, b), так как каждый из этих дней он будет надевать по одному красному и по одному синему носку.
После этого у него останутся либо только красные носки, либо только синие носки, либо не останется носков вовсе. Поэтому второе ответное число это max((a - min(a, b)) / 2, (b - min(a, b)) / 2).
Асимптотика решения — O(1).
581B — Элитные дома
Данная задача решается следующим образом. Пойдем по массиву справа налево и будем поддерживать в переменной maxH максимальную высоту дома, который мы уже рассмотрели. Тогда ответом для i-го дома будет число max(0, maxH + 1 - hi), где hi количество этажей в i-м доме.
Асимптотика решения — O(n), где n — количество домов.
581C — Развитие навыков
Данную задачу можно решать несколькими способами. Рассмотрим самый понятный способ, который укладывается в заданное время.
Отсортируем заданный массив следующим образом — из двух чисел левее должно стоять то, к которому нужно добавить меньше единиц улучшений, чтобы оно стало кратно 10. Обязательно добавлять хотя бы одну единицу энергии. Например, если исходный массив {45, 30, 87, 26}, то после сортировки он должен выглядеть следующим образом — {87, 26, 45, 30}.
Теперь проитерируемся по отсортированному массиву слева направо по i от 1 до n. Пусть cur = 10 - (aimod10). Если cur ≤ k, присвоим ai = ai + cur, а из k вычтем cur, иначе, если cur > k выйдем из цикла.
Следующим шагом проитерируемся по массиву аналогичным образом.
Осталось посчитать ответ ans — проитерируемся по массиву по i от 1 до n и присвоим ans = ans + (ai / 10).
Асимптотика решения — O(n * log(n)), где n количество заданных навыков героя.
581D — Три логотипа
Данная задача решается несколькими способами, рассмотрим один из них.
Для начала подсчитаем суммарную площадь s данных нам прямоугольников. Тогда сторона ответного квадрата это sqrt(s). Если sqrt(s) не целое число, выводим -1. Иначе сделаем следующее.
Переберем порядок, в котором будем добавлять заданные прямоугольники в квадрат (это можно сделать с помощью next_permutation()), а также для каждого порядка переберем будем ли мы переворачивать текущий прямоугольник на 90 градусов или нет (это можно сделать с помощью двоичных масок). Изначально на каждой итерации квадрат c, в который мы добавляем прямоугольники ничем не заполнен (пустой).
Для каждого из добавляемых прямоугольников сделаем следующее — найдем самую верхнюю левую свободную клетку free в квадрате c (напомним, что мы также перебираем, поворачиваем ли мы прямоугольник на 90 градусов или нет). Попытаемся наложить текущий прямоугольник в квадрат c, причем его левый верхний угол должен совпадать с клеткой free. Если текущий прямоугольник полностью помещается в квадрат c и не накладывается на уже занятую каким-то другим прямоугольником клетку, заполним соответствующие клетки в квадрате c нужной буквой.
Если после добавления всех трех прямоугольников не нарушилось ни одно из условий и весь квадрат c оказался заполненным мы нашли ответ — выводим квадрат c.
Если ответ не нашелся ни для одной перестановки прямоугольников — выводим -1.
Для произвольного количества прямоугольников k асимптотика решения — O(k! * 2k * s), где s — суммарная площадь заданных прямоугольников.
Также данная задача для 3 прямоугольников имеет решение с разбором случаев с асимптотикой O(s), где s — суммарная площадь заданных прямоугольников.
581E — Кодзиро и Furrari
Пусть f — стартовая позиция, а e — конечная. Для удобства реализации и дальнейших рассуждений добавим заправку в точке e типа 3.
Первое замечание: никогда нет смысла идти налево из стартовой точки ведь мы в ней уже стоит с полным баком лучшего бензина. Замечание верно и для любой заправки, в которой мы можем оказаться (если в оптимальном ответе мы должны пойти налево до некоторой заправки pv, то почему бы не выкинуть весь путь из pv в текущую заправку v и обратно и от этого ответ станет только лучше). Теперь поймем как нам следует действовать если мы находимся в некоторой заправке v.
Первый случай: на расстоянии не более чем s находится заправка в качеством бензина не хуже, чем в нашей (можно считать, что в момент старта мы находимся на заправке типа 3, но добавлять такую заправку нельзя). Зафиксируем ближайшую из них nv (ближайшую справа, так как мы уже поняли, что идти влево нет смысла). В этом случае дозаправимся так, чтобы возможно было доехать до nv. И поедем в nv.
Второй случай: из нас достижимы только заправки с худшим качеством. Заметим, что это возможно лишь в случае, если мы находимся в заправке типа 2 или 3. В случае заправки второго типа у нас нет никакого выбора кроме как заправиться на полную и поехать в самую последнюю достижимую вершину (то есть вершину на расстоянии не более чем s). Если же мы находимся в вершине типа 3, то нужно идти по возможности в самую дальнюю вершину типа 2, если же такой нет то идти в самую дальнюю типа 1. Эти рассуждения верны в силу того, что нам в первую очередь необходимо минимзировать бензин типа 1, а при равенстве типа — 2. Как можно дальше нужно идти потому, что бензин в нашей вершине строго лучше достижимых, а тип 2 нужно выбирать, поскольку если мы можем доехать до типа 1 и он находится правее заправки типа 2, то мы можем это сделать, проехав через заправку типа 2, возможно улучшив ответ.
Это основные рассуждения необходимые для решения задачи. Далее будем считать диманику на всех суффиксах i заправок — ответ на задачу если мы стартуем из заправки i с пустым баком. Переходы мы должны сделать, рассматривая описанные выше случаи. Для пересчета динамики в v нам нужно взять значение динамики в nv и сделать пересчет в зависимости от случая. Если случай 1, то нужно просто к соответствующему значению прибавить расстояние d от v к nv. Если это случай 2 и мы в заправке типа 2 нужно ко второму значению ответа прибавить s, а из первого вычесть s–d. Если это случай 2 и мы в заправке типа 3, то нужно из значения, определяемого типом заправки nv вычесть s–d.
Теперь, чтобы ответить на конкретный запрос стартовой позиции нужно найти первую завправку правее стартовой позиции, сделать один переход и взять уже посчитанное значение динамики (конечно, пересчитав это значение в соответствии с вышеописанным).
Сложность решения по времени: O(n logn) или O(n) в зависимости от того как искать позицию в списке заправок (первое в случае бинпоиска, второе в случае двух указателей). Сложность решения по памяти: O(n).
581F — Зубликанцы и мумократы
Пусть количество листьев дерева (вершин степени 1) равно c. По условию c четно. Если вершин всего 2, то ответ 1. Иначе в дереве есть вершина не лист, подвесим дерево за эту вершину.
Теперь будем считать 2 динамики. Первая z1[v][cnt][col] — наименьшее количество разноцветных ребер в поддереве с корнем в вершине v, если вершина v уже покрашена в цвет col (col равен 0 либо 1), а среди листьев поддерева вершины v должно быть ровно cnt вершин цвета 0. Если мы в листе, то это значение легко посчитать. Если мы не в листе посчитаем значение с помощью вспомогательной динамики z1[v][cnt][col]: = z2[s][cnt][col], где s — первый сын в списке смежности вершины v.
Вторая динамика z2[s][cnt][col] нам нужна для того, чтобы распределить cnt листьев цвета 0 среди поддеревьев сыновей вершины v. Для подсчета z2[s][cnt][col] переберем цвет сына s — ncol и количество листьев i цвета 0, которые будут располагаться в поддереве вершины s и пересчитаем значение следующим образом z2[s][cnt][col] = min(z2[s][cnt][col], z2[ns][cnt–a][col] + z1[s][a][ncol] + (ncol! = col)), где ns — следующий после s сын вершины v. Заметим, что не имеет смысла брать a больше, чем количество листьев в поддереве s, ну и тем более — больше количества вершин в поддереве sizes (поскольку у нас просто не хватит листьев для покраски).
Оценка сверху для такой динамики O(n3). Покажем, что в сумме решение будет работать за O(n2). Посчитаем количество переходов: 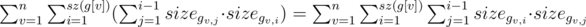 . Заметим, что в последнюю сумму каждая пара вершин (x, y) войдет ровно один раз, именно при наименьшем общем предке v = lca(x, y). Таким образом переходов не более O(n2).
. Заметим, что в последнюю сумму каждая пара вершин (x, y) войдет ровно один раз, именно при наименьшем общем предке v = lca(x, y). Таким образом переходов не более O(n2).
Сложность решения по времени и памяти: O(n2).
Всем привет!
Раньше мой вклад в развитие Codeforces ограничивался подготовкой раундов (Codeforces Round 288 (Div. 2), Codeforces Round 293 (Div. 2), Codeforces Round 297 (Div. 2)). Но месяц назад я присоединился к работе чудесной команды Codeforces во главе с Михаилом Мирзаяновым (MikeMirzayanov). Традиционно, чтобы вникнуть во все тонкости этого проекта, моя работа началась с системы Polygon. Хотелось бы рассказать Вам о ее изменениях.
Напомню, что Polygon — это система для подготовки задач по программированию. Именно в ней подготавливаются все задачи к раундам Codeforces и многим другим олимпиадам. Системой Polygon могут пользоваться все желающие в любой момент времени.
Для редактирования файлов в Polygon теперь используется Ace Editor. В нем есть приятная глазу подсветка синтаксиса и автодополнение (нужно нажать Ctrl + Space). В скором времени планируется внедрить этот редактор и в Codeforces.
Привет, Codeforces!
30 июня 2015 года в 18:00 MSK состоится очередной раунд Codeforces #311 для участников из второго дивизиона. Традиционно, участники из первого дивизиона приглашаются поучаствовать в соревновании вне конкурса. Обратите внимание на необычное время начала раунда!
Это мой четвертый Codeforces раунд, желаю всем быстрых и главное полных решений!
Хотелось бы сказать большое спасибо Максиму Ахмедову (Zlobober) за помощь в подготовке задач, Марии Беловой (Delinur) за перевод условий на английский, Михаилу Мирзаянову (MikeMirzayanov) за замечательные системы Codeforces и Polygon и за помощь в придумывании задач, а также моим друзьям Илье Лось (IlyaLos) и Данилу Сагунову (danilka.pro) за прорешивание задач и вычитывание условий.
Участникам будет предложено пять задач и два часа на их решение. Разбалловка будет объявлена позднее.
UPD Разбалловка задач стандартная 500-1000-1500-2000-2500. Всем удачи!
UPD2 Соревнование завершено! Всем спасибо!
UPD3 здесь вы можете найти разбор задач.
557A — Илья и дипломы
Данную задачу можно решать несколькими способами, рассмотрим один из них — разбор случаев.
Если max1 + min2 + min3 ≤ n, тогда оптимальный ответ (n - min2 - min3, min2, min3).
Иначе, если max1 + max2 + min3 ≤ n, тогда оптимальный ответ (max1, n - max1 - min3, min3).
Иначе, оптимальный ответ (max1, max2, n - max1 - max2).
Данное решение верно, так как по условию задачи гарантируется, что min1 + min2 + min3 ≤ n ≤ max1 + max2 + max3.
Асимптотика решения — O(1).
557B — Паша и чай
Данная задача также может быть решена несколькими способами. Рассмотрим самый простой из них, который укладывается в заданные ограничения.
Сначала отсортируем все чашки по неубыванию их объемов. В силу жадных соображений верно, что отсортированные чашки с номерами от 1 до n будут отданы девочкам, а с номерами от n + 1 до 2 * n будут отданы мальчикам.
Теперь сделаем бинарный поиск с итерациями по объему чая, который будет налит каждой девочке. Пусть на текущей итерации (lf + rg) / 2 = mid. Тогда, если для всех i от 1 до n верно, что mid ≤ ai, а для всех i от n + 1 до 2 * n верно, что 2 * mid ≤ ai, тогда нужно поднять нижнюю границу бинарного поиска, то есть lf = mid. Иначе, нужно опустить верхнюю границу бинарного поиска, то есть rg = mid.
Асимптотика решения — O(n * log(n)), где n — количество чашек.
557C — Артур и стол
Данная задача решается следующим образом. Изначально, отсортируем все ножки по неубыванию их длин. Также нам понадобится массив cnt[].
Переберем длину ножек, на которых будет стоять стол, начиная с наименьшей. Пусть она равна maxlen. Количество единиц энергии, которое нам для этого потребуется будем хранить в переменной cur.
Очевидно, что необходимо открутить все ножки с длинами большими maxlen. Так как массив отсортирован, то, чтобы посчитать количество единиц энергии, которое понадобится для этого, можно воспользоваться суммой энергии на суффиксах. Прибавим это количество к cur.
Если количество ножек длины maxlen не строго больше количества оставшихся ножек, нужно открутить сколько то ножек с длиной меньшей, чем maxlen. Для этого воспользуемся массивом cnt[]. В cnt[i] будем хранить количество ножек со сложностью откручивания равной i. В нем будет содержаться информация о уже рассмотренных ножках.
Будем перебирать сложность откручивания от единицы и откручивать ножки с такими сложностями (прибавляя эти сложности в переменную cur), пока количество ножек с длиной maxlen не станет строго больше количества оставшихся ножек.
Когда ножек длины maxlen станет строго больше половины оставшихся ножек обновим переменной cur ответ.
Асимптотика решения — O(n * d), где n — количество ножек, а d — разность между максимальным и минимальным количеством единиц энергии, которое может понадобится, чтобы открутить какие-то ножки.
557D — Виталий и цикл
Для решения данной задачи нам нужен поиск в ширину или в глубину, который будет проверять каждую компоненту связности графа на двудольность. Очевидно, что количество ребер, которое нужно добавить в граф, чтобы получился нечетный цикл, не превышает трех.
Ответ на задачу равен трем в том случае, когда в графе нет ни одного ребра. Тогда количество способов добавить три ребра в граф, чтобы получился цикл нечетной длины равно количеству способов выбрать три вершины из n (будем соединять ребрами именно эти вершины). Это число равно n * (n - 1) * (n - 2) / 6.
Ответ на задачу равен двум, если в графе нет компонент связности с количеством вершин большим чем два. Как найти количество способов?
Пусть cnt2 — количество компонент связности, которые состоят из двух вершин. Тогда выберем любые две вершины, соединенные ребром. Эти две вершины и ребро, соединяющее их точно войдут в ответ. Осталось выбрать любую другую вершину и соединить ее двумя ребрами с выбранными ранее соединенными вершинами. То есть количество способов равно cnt2 * (n - 2).
Остался случай, когда в графе есть хотя бы одна компонента связности с количеством вершин большим двух. Воспользуемся, например, поиском в глубину для каждой компоненты и будем красить вершины в два цвета. В массиве color[] будем запоминать цвет вершин, изначально все вершины непокрашены.
Пусть в поиске в глубину мы идем из вершины v в вершину to (вершина v уже точно покрашена в какой-то цвет). Если вершина to не покрашена, тогда покрасим ее в цвет, противоположный цвету вершины v и запустим поиск в глубину от вершины to. Если вершина to уже покрашена в цвет, не равный цвету вершины v, пропустим ее. Если же color[v] = color[to], тогда выведем "0 1" и закончим алгоритм. Это означает то, что в графе уже есть цикл нечетной длины.
После запуска поиска в глубину для всех компонент, если не нашлось цикла нечетной длины, нужно добавить лишь одно ребро, чтобы такой цикл получился. Чтобы посчитать количество способов его добавить, нужно проитерироваться по компонентам связности, чей размер больше двух. Все они двудольны, так как нет нечетного цикла в графе.
Если в текущей компоненте связности cnt1 вершин в одной доле и cnt2 вершин в другой доле, тогда к количеству способов нужно прибавить cnt1 * (cnt1 - 1) / 2 и cnt2 * (cnt2 - 1) / 2.
Асимптотика решения — O(n + m), где n — количество вершин в графе, а m — количество ребер.
557E — Аня и полупалиндром
Данная задача решается с помощью динамического программирования.
Сначала насчитаем матрицу good[][]. В good[i][j] запишем true, если подстрока с позиции i до позиции j полупалиндром. Иначе запишем в good[i][j]false. Это можно сделать, перебирая "середину" полупалиндрома и расширяя ее влево и вправо. Возможны 4 случая "середины", но опустим их, так как они достаточно просты.
Теперь будем складывать в бор суффиксы заданной строки. Также будем хранить массив cnt[]. В cnt[v] будем хранить сколько полупалиндромов заканчивается в вершине бора v. Пусть сейчас мы записываем в бор суффикс, который начинается в позиции i, кладем символ, стоящий в строке в позиции j, и переходим в вершину v. Тогда, если good[i][j] = true, нужно сделать cnt[v] + + .
Теперь простым обходом в глубину посчитаем для каждoй вершины sum[v] — сумму чисел, стоящих в вершине v и во всех ее поддеревьях.
Осталось только восстановить ответ. Запустимся из корня бора. Будем хранить его в строке ans. В переменной k храним номер искомой подстроки. Пусть сейчас мы стоим в вершине v, по символу 'a' можем перейти в вершину toa, а по символу 'b' — в вершину tob.
Тогда, если sum[toa] ≤ k, сделаем ans + = 'a' и перейдем в вершину toa. Иначе, нужно сделать следующее: k — = sum[toa], ans + = 'b' и перейдем в вершину tob.
Когда k станет ≤ 0 выведем получившуюся строку ans и закончим алгоритм.
Асимптотика решения — O(szalph * n2), где szalph — размер входного алфавита (в данной задаче он равен двум), а n — длина заданной строки.
Привет, Codeforces!
26 марта 2015 года в 19:30 MSK состоится очередной раунд Codeforces #297 для участников из второго дивизиона. Традиционно, участники из первого дивизиона приглашаются поучаствовать в соревновании вне конкурса.
Это мой уже третий Codeforces раунд, надеюсь, я вам еще не сильно надоел.
Хотелось бы сказать большое спасибо Максиму Ахмедову (Zlobober) за помощь в подготовке задач, Марии Беловой (Delinur) за перевод условий на английский, Михаилу Мирзаянову (MikeMirzayanov) за замечательные системы Codeforces и Polygon и за идеи некоторых задач, а также моим старинным друзьям Павлу Холкину (HolkinPV), Илье Лось (IlyaLos), Виталию Кудасову (kuviman) и Артуру Свечникову (ikar) за прорешивание задач и вычитывание условий.
Участникам будет предложено пять задач и два часа на их решение. Разбалловка будет объявлена позднее.
UPD Стоимость задач будет плавной динамической с шагом в 250 баллов. Подробнее об этом вы можете прочитать здесь. Задачи будут расположены в порядке предполагаемого возрастания сложности.
UPD2 Соревнование завершено! Спасибо всем кто участвовал!
UPD3 Разбор уже ждет вас здесь.
UPD4 Поздравляем победителей!
525A — Виталий и пирожок
Для решения данной задачи будем использовать массив cnt[]. В нем будем хранить сколько ключей каждого типа мы уже нашли в комнатах, но пока не использовали, а ответ будем считать в переменной ans.
Проитерируемся по строке s. Если текущий элемент строки si строчная буква (ключ), увеличим cnt[si] на единицу. Если текущий элемент строки si прописная буква (дверь) возможны два случая. Если cnt[tolower(si)] > 0, тогда уменьшим cnt[tolower(si)] на единицу, иначе увеличим ans на единицу. Осталось вывести ответ.
Асимптотика решения — O(|s|), где |s| — длина строки s.
525B — Паша и строка
Сначала нужно понять следующий факт — неважно в каком порядке выполнять перевороты, ответ от этого не изменится.
Пусть элементы строки проиндексированы начиная с единицы. Для решения задачи посчитаем сколько переворотов будет начинаться в каждой из позиций строки. Потом насчитаем массив sum[]. В sum[i] будем хранить количество переворотов подстрок, которые начинаются в позициях, не превышающих i.
Теперь проитерируемся по i от 1 до n / 2 и, если sum[i] нечетно, поменяем местами элементы строки si и sn - i + 1. Выведем ответ — получившуюся строку s.
Асимптотика решения — O(n + m), где n — длина строки s, m — количество переворотов.
525C — Илья и палочки
Данная задача решается жадным образом. Насчитаем массив cnt[]. В cnt[i] будем хранить сколько у нас есть палочек длины i.
Теперь проитерируемся по длинам палочек (len) от максимальной длины до минимальной. Если cnt[len] нечетно и есть палочки длины len - 1 (то есть cnt[len - 1] > 0), сделаем cnt[len]-- и cnt[len - 1]++. Если же cnt[len] нечетно и палочек длины len - 1 нет (то есть cnt[len - 1] = 0), просто сделаем cnt[len]--. Таким образом, мы корректно сделали все нужные спиливания и гарантировали, что cnt[len] четные.
После этого вновь нужно пройти по длинам палочек аналогичным циклом и жадным образом объединять пары из 2 палочек одинаковых длин в четверки. Это и будут длины сторон ответных прямоугольников, осталось сложить их площади. В конце могут остаться две палочки без пары, их в ответе учитывать не нужно.
К примеру, если cnt[5] = 6, cnt[4] = 4, cnt[2] = 4, нужно объединить эти палочки в прямоугольники следующим образом — (5, 5, 5, 5), (5, 5, 4, 4), (4, 4, 2, 2). Две оставшиеся палочки длины 2 на ответ не влияют, так как их не с кем объединить.
Асимптотика решения — O(n + maxlen - minlen), где n — количество палочек, maxlen — максимальная длина палочки, minlen — минимальная длина палочки.
525D — Артур и стены
Для решения данной задачи нужно заметить следующий факт. Если в каком-то квадрате размера 2 × 2 в заданной матрице есть ровно одна звездочка, ее точно нужно заменить на точку. То есть если в матрице из точек и звездочек нет квадрата 2 × 2, в котором ровно одна звездочка (остальные точки), то все максимальные по размеру связные по стороне области из точек представляют собой прямоугольники.
Теперь решим задачу с помощью обхода в ширину. Пройдем по всем звездочкам матрицы, и, если есть квадрат 2 × 2, содержащий текущую звездочку, а остальные элементы этого квадрата точки, заменим эту звездочку на точку и положим эту позицию в очередь. Затем напишем стандартный обход в ширину, в котором будем заменять звездочки на точки во всех получающихся квадратах 2 × 2, в которых ровно одна звездочка.
Асимптотика решения — O(n * m), где n и m — размеры заданной матрицы.
525E — Аня и кубики
Для решения данной задачи воспользуемся методом meet - in - the - middle. Отсортируем заданный массив по возрастанию и разобьем пополам. В первой половине оставим первые n / 2 элементов, во второй все остальные.
Переберем все подмаски всех масок элементов из первой половины. То есть переберем какие кубики из первой половины мы возьмем и на какие из них наклеим восклицательные знаки. Таким образом мы переберем все возможные суммы, которые мы можем набрать с помощью кубиков из первой половины.
Пусть для текущей подмаски мы наберем сумму sumlf, используя tlf восклицательных знаков. Для хранения всех сумм используем ассоциативные массивы map < long long > cnt[k+1], где k — количество восклицательных знаков, которое у нас есть изначально. Тогда для текущей подмаски нужно сделать cnt[tlf][sumlf]++.
После этого, аналогичным образом, переберем все подмаски всех масок элементов из правой части. Пусть для текущей подмаски сумма равна sumrg, а количество использованных восклицательных знаков trg. Тогда в левой части нам нужно набрать сумму (s - sumrg), используя не более (k - trg) восклицательных знаков, где s — сумма, которую необходимо набрать по условию задачи. Тогда переберем сколько восклицательных знаков будем использовать в левой части (пусть это будем переменная cur) и прибавим к ответу cnt[cur][s - sumrg].
Для ускорения работы программы можно сначала проверить есть ли такой элемент в нашем массиве, то есть только если cnt[cur].count(s - sumrg) = true увеличивать ответ. Для перебираемых подмасок можно отсекать перебор по текущей сумме для подмаски и по количеству восклицательных знаков для текущей подмаски. Также понятно, что не имеет смысле наклеивать восклицательные знаки на кубики на которых написаны числа большие 18, так как 19! точно больше чем 1016, что по условию является верхним ограничением для s.
Асимптотика решения — O(3((n + 1) / 2) * log(maxcnt) * k), где n — количество кубиков, maxcnt — максимальный размер ассоциативного массива, k — количество восклицательных знаков.
517A — Виталий и строки
Для решения данной задачи можно было, например, найти строку next, лексикографически следующую за строкой s и проверить, что строка next лексикографически меньше строки t. Если строка next оказалась меньше строки t, выведем ее и закончим алгоритм. Если же строка next совпала со строкой t, следовало вывести No such string.
Чтобы найти строку next, лексикографически следующую за s, нужно сначала найти максимальный суффикс строки s, состоящий из букв 'z', заменить все буквы 'z' в этом суффиксе на буквы 'a', а затем букву, стоящую перед этим суффиксом, увеличить на единицу. То есть, если перед суффиксом стояла, например, буква 'd', ее следует заменить на букву 'e'.
Асимптотика решения — O(|s|), где |s| — длина строки s.
517B — Таня и поздравление
Для решения данной задачи, сначала насчитаем массив cnt[], где cnt[c] — сколько раз буква c встречалась в строке t. Будем считать два числа ans1 и ans2 — сколько раз Таня прокричит УРА! и сколько раз Таня произнесет ОПА.
Теперь проитерируемся по строке s, и если cnt[s[i]] > 0, то прибавим к ans1 единицу и уменьшим cnt[s[i]] на единицу.
Теперь вновь проитерируемся по строке s. Пусть c это буква равная s[i], но в обратном ей регистре. То есть если s[i] = 'w', то c = 'W'. Теперь, если cnt[c] > 0, то прибавим к ans2 единицу и уменьшим cnt[с] на единицу.
Осталось вывести два числа — ans1 и ans2.
Асимптотика решения — O(|s| + |t|), где |s| — длина строки s, а |t| — длина строки t.
517C — Аня и смартфон
Для решения данной задачи будем хранить два массива — a[] и pos[]. В массиве a[] будем хранить текущий порядок расположения иконок, то есть в a[i] хранится номер приложения, иконка которого стоит на i-м месте. В массиве pos[] будем хранить на каком месте в списке находятся иконки, то есть в pos[i] хранится в какой позиции массива a[] находится иконка приложения номер i. Будем считать ответ в переменной ans.
Проитерируемся по приложениям, которые нужно открыть. Пусть текущее приложение имеет номер num. Тогда нужно к ans прибавить pos[num] / k + 1 (первый член суммы — количество движений пальцем, чтобы долистать до нужного экрана, второй член суммы — одно движение пальцем для открытия приложения). Теперь, если иконка приложения номер num не стоит на первом месте в списке приложений, сделаем следующее — поменяем местами значения a[pos[num]] и a[pos[num] - 1] и обновим значения pos[] для иконок приложений, чьи номера равны a[pos[num]] и a[pos[num] - 1].
Асимптотика решения — O(n + m), где n — количество приложений, m — количество запросов на запуск приложений.
517D — Илья и эскалатор
Для решения данной задачи воспользуемся динамическим программированием. Будем хранить двумерный массив z типа double . В z[i][j] будет храниться вероятность того, что через i секунд j человек зашли на эскалатор.
В динамике будут следующие переходы. Если j = n, то есть все n людей уже находятся на эскалаторе, тогда сделаем переход z[i + 1][j] + = z[i][j]. Иначе, либо j-й человек зайдет на эскалатор в i + 1 секунду, то есть z[i + 1][j + 1] + = z[i][j] * p, либо j-й человек останется на месте, то есть z[i + 1][j] + = z[i][j] * (1 – p).
Осталось посчитать ответ (математическое ожидание количества людей на эскалаторе) — это сумма по j от 0 до n включительно z[t][j] * j.
Асимптотика решения — O(t * n), где t — на какой момент нужно посчитать матожидание, n — сколько людей сначала стоит у эскалатора.
517E — Артур и вопросы
Сначала заметим следующий факт. Возьмем первые две суммы a1 + a2 + ... + ak и a2 + a3 + ... + ak + 1. Должно выполниться неравенство a1 + a2 + ... + ak < a2 + a3 + ... + ak + 1. Если перенести справа налево все элементы кроме ak + 1, все они сократятся и останется a1 < ak + 1. Если выписать далее все подобные суммы получится, что последовательность распадается на k непересекающихся цепочек: a1 < ak + 1 < a2k + 1 < a3k + 1..., a2 < ak + 2 < a2k + 2 < a3k + 2..., ..., ak < a2k < a3k....
Будем решать задачу для каждой цепочки отдельно. Рассмотрим первую цепочку a1, ak + 1, a2k + 1.... Проитерируемся по ней, и найдем все пары индексов i, j (i < j), что a[i] и a[j] это числа, а не вопросы, в заданной последовательности, а для всех k от i + 1 до j - 1 в a[k] стоят знаки вопроса. Тогда понятно, что все эти вопросы нужно заменить на числа таким образом, чтобы не нарушить условие возрастания и при этом минимизировать сумму модулей поставленных чисел.
Понятно, что между индексами i и j стоит j - i - 1 знак вопроса, их можно заменить на a[j] - a[i] - 1 чисел. Если j - i - 1 > a[j] - a[i] - 1, тогда нужно вывести Incorrect sequence и закончить алгоритм. Иначе нужно жадным образом заменить все эти вопросы на числа.
Здесь возможно несколько случаев. Рассмотрим один из них, когда a[i] > = 0 и a[j] > = 0. Пусть текущая цепочка (3, ?, ?, ?, 9), i = 1, j = 5. Знаки вопроса нужно заменить следующим образом — (3, 4, 5, 6, 9). Осталось два случая, когда a[i] < = 0, a[j] < = 0, и случай, когда a[i] < = 0, a[j] > = 0. В таких случаях нужно поступать жадным образом, аналогично первому, не нарушая условие возрастания и минимизируя сумму модулей поставленных чисел.
Асимптотика решения — O(n), где n — количество элементов в заданной последовательности.
517F — Паша и труба
Будем решать данную задачу поэтапно. Сначала насчитаем два двумерных массива частичных сумм sumv[][] и sumg[][]. В sumv[i][j] хранится сколько решеток стоит в столбце j начиная со строки 1 до строки i. В sumg[i][j] хранится сколько решеток стоит в строке i начиная со столбца 1 до столбца j.
Посчитаем ans0 — сколько труб без изгибов можно проложить. Посчитаем количество вертикальных труб — проитерируемся по j от 2 до m — 1 и, если sumg[n][j] — sumg[n][0] = 0 (то есть в этом столбце нет ни одной решетки), прибавим к ans0 единицу. Аналогично посчитаем количество горизонтальных труб.
Посчитаем ans1 — сколько труб с 1 изгибом можно проложить. Переберем клетку, в которой будет изгиб (по условию эта клетка не должна лежать на краях поля). Возможны четыре случая: труба начинается слева, доходит до текущей перебираемой клетки и поворачивает вверх; труба начинается сверху, доходит до текущей перебираемой клетки и поворачивает вправо; труба начинается справа, доходит до текущей перебираемой клетки и поворачивает вниз; труба начинается снизу, доходит до текущей перебираемой клетки и поворачивает влево.
Рассмотрим первый случай — труба начинается слева, доходит до текущей перебираемой клетки и поворачивает вверх. Пусть клетка поворота находится в i-й строке и j-м столбце. Тогда к ans1 нужно прибавить единицу, если (sumg[i][j] — sumg[i][0]) + (sumv[i][j] — sumv[0][j]) = 0. Для оставшихся случаев нужно сделать аналогичным образом.
Осталось посчитать ans2 — сколько труб с 2 изгибами можно проложить. Поступим следующим образом. Посчитаем сколько труб начинаются сверху и заканчиваются сверху или снизу, и прибавим это число к ans2. Затем повернем матрицу три раза на 90 градусов и после каждого поворота прибавим к ans2 количество труб, начинающихся сверху и заканчивающихся сверху или снизу. Если считать таким образом, каждая труба посчитается по два раза, поэтому ans2 нужно поделить пополам.
Как посчитать для текущей матрицы сколько труб начинаются сверху и заканчиваются сверху или снизу. Насчитаем четыре двумерных массива lf[][], rg[][], sumUp[][], sumDown[][]. Пусть i — номер строки, j — номер столбца текущей клетки. Тогда в позиции (i, lf[i][j]) в матрице находится ближайшая слева решетка для клетки (i, j), а в позиции (i, rg[i][j]) в матрице находится ближайшая справа решетка для клетки (i, j). В sumUp[i][j] должно быть число — сколько столбцов без решеток содержится в подматрице от (1, 1) до (i, j) исходной матрицы. В sumDown[i][j] должно быть число — сколько столбцов без решеток содержится в подматрице от (i, 1) до (n, j) исходной матрицы. Осталось перебрать клетку, в которой произойдет первый поворот трубы (она шла сверху и повернула направо или налево), проверить что в столбце j над этой клеткой нет решеток, с помощью массивов lf и rg узнать насколько труба могла идти налево или направо и с помощью массивов sumUp и sumDown аккуратно пересчитать ответ.
Осталось вывести число ans1 + ans2 + ans3.
Асимптотика решения — O(n * m * const), где n — количество строк в заданной матрице, m — количество столбцов в заданной матрице, const принимает различные значения в зависимости от реализации, в решении из разбора const = 10.
Привет, Codeforces!
24 февраля 2015 года в 19:30 MSK состоится очередной раунд Codeforces #293 для участников из второго дивизиона. Традиционно, участники из первого дивизиона приглашаются поучаствовать в соревновании вне конкурса.
Это мой второй Codeforces раунд, и я надеюсь, что Вам понравятся задачи, и все пройдет хорошо.
Хотелось бы сказать большое спасибо Максиму Ахмедову (Zlobober) за помощь в подготовке задач, Марии Беловой (Delinur) за перевод условий на английский, Михаилу Мирзаянову (MikeMirzayanov) за замечательные системы Codeforces и Polygon и за идеи некоторых задач, а также моим дорогим друзьям Павлу Холкину (HolkinPV), Артуру Свечникову (ikar) и Виталию Кудасову (kuviman) за прорешивание задач.
Раунд будет немного необычным — участникам будет предложено шесть задач и два с половиной часа на их решение.
UPD Разбалловка задач 500-1000-1500-2000-2500-2500. Всем удачи!
UPD2 Соревнование завершено! Всем спасибо!
UPD3 Разбор вы можете найти здесь.
UPD4 Поздравляем победителей!
508A — Паша и пиксели
Для решения данной задачи заведем матрицу типа bool размера n на m. В ячейке (x, y) данной матрицы будем ставить значение true, если соответствующая клетка окрашена в черный цвет.
Пусть на k-том ходу Паша красит пиксель в позиции (i, j). Тогда на этом ходу игра закончится, если образуется квадрат 2 × 2 из черных клеток, а клетка (i, j) будет левым нижним, левых верхним, правым нижним или правым верхним углом этого квадрата. Только такие квадраты и нужно проверить на текущем ходу. Если таких квадратов не образуется за k ходов, выводим 0. Асимптотика решения — O(k), где k — количество ходов.
508B — Антон и та самая валюта
Так как изначально число нечетное (значит последняя цифра в нем нечетная), а необходимо сделать четное, то понятно, что необходимо поменять местами последнюю цифру с какой-то четной. Стоить отметить, что так как число очень большое, удобно его хранить в строке. Так как необходимо сделать максимально возможное число, сделаем следующее.
Переберем все цифры в числе, начиная от старшей, и если встретим четную цифру, которая меньше последней цифры числа — поменяем их местами, это и есть ответ. Если такой цифры не нашлось, переберем все цифры числа в порядке от предпоследней до первой (до старшей цифры числа), и если встретим четную — поменяем местами ее и последнюю цифру числа. Ответ не найдется лишь в одном случае, если в числе нет четных цифр. В таком случае выводим - 1. Асимптотика решения — O(n), где n — длина числа.
508C — Аня и привидения
Данная задача решается с помощью принципа жадности. Так как приходы всех привидений заданы в хронологическом порядке — будем перебирать их по очереди.
Будем хранить массив, в котором будем помечать моменты времени, в которые мы зажигали свечи (например, ставить в соответствующую позицию 1). Тогда для каждого нового привидения узнаем количество свечей, которые будут гореть во время его посещения по данному массиву.
Если привидение пришло в момент времени wi, проитерируемся по нашему массиву от wi - 1 до wi - t, где t — количество секунд, которое горит свеча, и посчитаем количество единиц. Если это количество не меньше, чем r, перейдем к следующему привидению. Иначе, проитерируемся по массиву от wi - 1 до wi - t, и, если в текущее время свеча еще не зажигалась — сделаем это, и поставим в эту позицию 1. Это нужно делать, пока количество единиц в этом отрезке массива не станет равно r. Если так сделать нельзя на какой — то итерации, то выводим - 1.
В конце нужно просто пройти по нашему массиву, и посчитать количество зажженных свечей, то есть единиц в массиве. Асимптотика решения — O(mt), где m — количество привидений, t — количество секунд, в течении которого горит одна свеча.
508D — Таня и пароль
В данной задаче входные данные сначала нужно представить в виде ориентированного графа. Вершинами в данном графе являются все возможные строки из двух символов — строчных и прописных букв латинского алфавита, а также цифр. Тогда для всех заданных трехбуквенных строк si-ых, добавим ребро из si[0]si[1] в si[1]si[2].
Теперь осталось найти в данном графе эйлеров путь. Для этого можно воспользоваться алгоритмом Флери. Стоит отметить, что Эйлеров путь найдется, если количество вершин, у которых степень исхода и входа отличается на единицу, не более двух, а степени исхода и входа всех остальных вершин равны. Если Эйлеров путь не найдется, нужно вывести NO. Асимптотика решения — O(m), где m — число ребер в графе, а соответственно и число заданных подстрок, ведь от каждой подстроки в граф будет добавлено ровно одно ребро.
508E — Артур и скобки
Данная задача решается методом динамического программирования. Заведем квадратную матрицу Z размера n × n, где n — количество открывающихся скобок в последовательности. Основной идеей данной задачи является то, что если открывающаяся скобка стоит в позиции l, а соответствующая ей закрывающаяся скобка — в позиции r, то с позиции l + 1 до позиции r - 1 должна стоять правильная скобочная последовательность.
В нашей динамике первый параметр lf — номер открывающейся скобки, а второй rg — номер самой последней открывающейся скобки, которая может быть в правильной скобочной последовательности, которая будет находиться между открывающейся скобкой под номером lf и соответствующей ей закрывающейся.
Значением динамики будет — true (можно составить такую последовательность) или false (нельзя).
Будем писать ленивую динамику по этим двум параметрам (по отрезкам). Переберем cnt — сколько открывающихся и, соответственно, закрывающихся скобок будет стоять между открывающейся скобкой под номером lf и соответствующей ей закрывающейся. Если это количество попадает в нужный интервал для открывающейся скобки номер lf, запустим нашу динамику от двух отрезков — (lf + 1, lf + cnt) и (lf + cnt + 1, rg).
Если для обоих отрезков можно составить правильные скобочные последовательности, соответствующие входным данным, положим в Z[lf][rg] значение true. Чтобы восстановить ответ, нужно переходить из отрезка (lf, rg) в отрезки (lf + 1, lf + cnt) и (lf + cnt + 1, rg), если для их обоих возможно составить правильную скобочную последовательность и рекурсивно восстанавливать ответ. Если Z[0][n - 1] равно false, то нужно вывести IMPOSSIBLE. Асимптотика решения — O(n3).
UPD Данная задача может быть решена с помощью жадного алгоритма. Асимптотика решения O(n). Пример такого решения участника matrix.
| Название |
|---|










