| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 153 |
| 7 | djm03178 | 152 |
| 7 | adamant | 152 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
Hello, Codeforces!
I'd like to invite you to Codeforces Round #386 (Div. 2). It'll be held on Sunday, December 18 at 13:35 MSK and as usual Div. 1 participants can join out of competition. Note that round starts in the unusual time!
This round is held on the tasks of the municipal stage All-Russian Olympiad of Informatics 2016/2017 year in city Saratov. They were prepared by Olympiad center of programmers of Saratov SU.
Great thanks to Nikolay Kalinin (KAN) for helping me preparing the contest, to Tatiana Semenova (Tatiana_S) for translating the statements into English, to Mike Mirzayanov (MikeMirzayanov) for the great Codeforces and Polygon platform and to Vladimir Petrov (vovuh), Alexey Ripinen (Perforator), Mikhail Levshunov (Levshunovma), Mikhail Piklyaev (awoo), Aleksey Slutskiy (pyloolex), Ivan Androsov (BledDest), Oleg Smirnov (Oleg_Smirnov) and Roman Kireev (RoKi) for writing solutions and editorials.
It will be a little unusual round — you will be given seven problems and two and half hours to solve them. The scoring distribution will be 500-1000-1500-2000-2500-3000-3000. Good luck everyone!
UPD Editorial
UPD2 Congratulations to the winners!
Hello, Codeforces!
I'd like to invite you to Codeforces Round #375 (Div. 2). It'll be held on Monday, October 3 at 14:35 MSK and as usual Div. 1 participants can join out of competition. Note that round starts in the unusual time!
This round is held on the tasks of the school stage All-Russian Olympiad of Informatics 2016/2017 year in city Saratov. They were prepared by me and Mike Mirzayanov (MikeMirzayanov).
Great thanks to Gleb Evstropov (GlebsHP) for helping me preparing the contest and for the idea of the most tricky problem, which was specially made for this round, to Tatiana Semenova (Tatiana_S) for translating the statements into English and to Nikolay Kalinin (KAN) for writing solutions and very helpful advices.
It will be a little unusual round — you will be given six problems and two and half hours to solve them.
Score distribution 500-1000-1500-2000-2500-3000. Good luck everyone!
UPD Editorial
Soon...
Hello, Codeforces!
Educational Codeforces Round 15 will take place on 29 July 2016 at 18:00 MSK for the first and the second divisions.
The round will be unrated for all users and it will be held with extented ACM ICPC rules. You will have two hours to solve six problems. After that you will have one day to hack any solution you want. You will have access to copy any solution and test it locally.
We with Mike MikeMirzayanov Mirzayanov decided to prepare this Round, because Edvard Edvard Davtyan is very busy at his new job. Good luck and have fun!
UPD Competition completed! Thank you all! Editorial
Hello, Codeforces!
I'd like to invite you to Codeforces Round #354 (Div. 2). It'll be held on Wednesday, May 25 at 18:05 MSK (Moscow time) and Div. 1 participants can join out of competition. As usual round starts in the unusual time!!!
Me an Grigory AGrigorii Akhremenko prepared the tasks for this Round. It is the debut for Grigory as the problemsetter.
Great thanks to Gleb GlebsHP Evstropov for helping us preparing the contest, to Mike MikeMirzayanov Mirzayanov for the great Polygon platform and for Ilya IlyaLos Los and for Artur ikar Svechnikov for writing solutions.
The scoring distribution will be announced later. Good luck everyone!
UPD Score distribution 500-1000-1500-2250-2250
UPD2 Editorial
UPD3 Congratulations to the winners
UPD4 See you soon!=)
670A - Holidays
There are many ways to solve this problem. Let's talk about one of them. At first we need to write a function, which takes the start day of the year and calculate the number of days off in such year. To make it let's iterate on the days of the year and will check every day — is it day off or no. It is easy to show that if the first day of the year equals to the first day of the week (i.e. this day is Monday) in this year will be minimum possible number of the days off. If the first day of the year equals to the first day off of the week (i.e. this day is Saturday) in this year will be maximum possible number of the days off.
670B - Game of Robots
To solve this problem we need to brute how many identifiers will called robots in the order from left to right. Let's solve this problem in one indexing. Let the current robot will call i identifiers. If k - i > 0 let's make k = k - i and go to the next robot. Else we need to print a[k], where a is the array with robots identifiers and end our algorithm.
670C - Cinema
We need to use map-ом (let's call it cnt) and calculate how many scientists knows every language (i. e. cnt[i] equals to the number of scientists who know the language number i). Let's use the pair res, where we will store the number of \textit{very pleased} scientists and the number of \textit{almost satisfied} scientists. At first let res = make_pair(0, 0). Now we need to iterate through all movies beginning from the first. Let the current movie has the number i. Then if res < make_pair(cnt[b[i]], cnt[a[i]]) let's make res = make_pair(cnt[b[i]], cnt[c[i]]) and update the answer with the number of current movie.
670D1 - Magic Powder - 1
This problem with small constraints can be solved in the following way. Let's bake cookies one by one until it is possible. For every new cookie let's calculate val — how many grams of the magic powder we need to bake it. For this let's brute all ingredients and for the ingredient number i if a[i] ≤ b[i] let's make b[i] = b[i] - a[i], else let's make b[i] = 0 and val = val + a[i] - b[i]. When we bruted all ingredients if val > k than we can't bake more cookies. Else let's make k = k - val and go to bake new cookie.
670D2 - Magic Powder - 2
Here we will use binary search on the answer. Let's we check the current answer equals to cur. Then the objective function must be realized in the following way. Let's store in the variable cnt how many grams of the magic powder we need to bake cur cookies. Let's iterate through the ingredients and the current ingredient has the number i. Then if a[i]·cur > b[i] let's make cnt = cnt + a[i]·cur - b[i]. If after looking on some ingredient cnt becomes more than k the objective function must return false. If there is no such an ingredient the objective function must return true.
If the objective function returned true we need to move the left end of the binary search to the cur, else we need to move the right end of the binary search to the cur.
670E - Correct Bracket Sequence Editor
Let's solve this problem in the following way. At first with help of stack let's calculate the array pos, where pos[i] equals to the position of the bracket which paired for the bracket in the position i. Then we need to use two arrays left and right. Then left[i] will equals to the position of the closest to the left bracket which did not delete and right[i] will equals to the position of the closest to the right bracket which did not delete. If there are no such brackets we will store -1 in the appropriate position of the array.
Let's the current position of the cursor equals to p. Then if the current operation equals to \texttt{L} let's make p = left[p] and if the current operation equals to \texttt{R} let's make p = right[p]. We need now only to think how process the operation \texttt{D}.
Let lf equals to p and rg equals to pos[p]. If lf > rg let's swap them. Now we know the ends of the substring which we need to delete now. If right[rg] = = - 1 we need to move p to the left (p = left[lf]), else we need to move p to the right (p = right[rg]). Now we need to recalculate the links for the ends of the deleted substring. Here we need to check is there any brackets which we did not deleted to the left and to the right from the ends of the deleted substring.
To print the answer we need to find the position of the first bracket which we did not delete and go through all brackets which we did not delete (with help of the array right) and print all such brackets. To find the position of the first bracket which we did not delete we can store in the array all pairs of the ends of substrings which we deleted, then sort this array and find the needed position. Bonus: how we can find this position in the linear time?
670F - Restore a Number
At first let's find the length of the Vasya's number. For make this let's brute it. Let the current length equals to len. Then if len equals to the difference between the length of the given string and the number of digits in len if means that len is a length of the Vasya's number.
Then we need to remove from the given string all digits which appeared in the number len, generate three strings from the remaining digits and choose smaller string from them — this string will be the answer. Let t is a substring which Vasya remembered. Which three strings do we need to generate?
Let's write the string t and after that let's write all remaining digits from the given string in the ascending order. This string can be build only if the string t does not begin with the digit 0.
Let's write at first the smallest digit from the remaining digits which does not equal to 0. If we have no such a digit we can't build such string. Else we need then to write all digits with smaller than the first digit in the t in the ascending order, then write the string t and then write all remaining digits in the ascending order.
Let's write at first the smallest digit from the remaining digits which does not equal to 0. If we have no such a digit we can't build such string. Else we need then to write all digits with smaller than or equal to the first digit in the t in the ascending order, then write the string t and then write all remaining digits in the ascending order.
Also we need to separately consider the case when the Vasya's number equals to zero.
If the given n is odd the answer is 0, because the perimeter of any rectangle is always even number.
If n is even the number of rectangles which can be construct equals to n / 4. If n is divisible by 4 we will count the square, which are deprecated, because we need to subtract 1 from the answer.
Asymptotic behavior — O(1).
At first let's find the minimum in the given array and store it in the variable minimum. It is easy to understand, that we always can paint n * minimum squares. So we need to find such a minimum in the array before which staying the most number of elements, which more than the minimum. In the other words we need to find 2 minimums in the array which are farthest from each other (do not forget about cyclical of the array). If there is only one minumum we need to start paint from the color which stay in the array exactly after the minimum (do not forget about cyclical of the array too). It can be done with help of iterations from the left to the right. We need to store the position of the nearest minimum in the variable and update her and the answer when we meet the element which equals to minimum.
Asymptotic behavior — O(n), where n — the number of different colors.
Let's build the answer recursively. For k = 0 the answer is - 1 or + 1. Let we want to build the answer for some k > 0. At first let's build the answer for k - 1. As the answer for k let's take four copies of answer for k - 1 with inverting of values in last one. So we have some fractal with 2 × 2 base: 00, 01. Let's prove the correctness of such building by induction. Consider two vector from the top (down) half: they have zero scalar product in the left half and in the right, so the total scalar product is also equals to zero. Consider a vector from the top half and from the down: their scalar products in the left and the right halfs differs only in sign, so the total scalar product is also zero.
Note the answer is also is a matrix with element i, j equals to \texttt{+} if the number of one bits in number i|j is even.
Complexity O((2k)2).
At first let's unite all segments which are in same verticals or horizontals. Now the answer to the problem is the sum of lengths of all segments subtract the number of intersections. Let's count the number of intersections. For this let's use the horizontal scan-line from the top to the bottom (is can be done with help of events — vertical segment is open, vertical segment is close and hadle horizontal segment) and in some data structure store the set of x-coordinates of the open segments. For example we can use Fenwick tree with precompression of the coordinates. Now for current horizontal segment we need to take the number of the opened vertical segmetns with value x in the range x1, x2, where x — vertical where the vertical segment are locating and x1, x2 — the x-coordinates of the current horizontal segment.
Asymptotic behavior: O(nlogn).
Consider slow solution: for operations of the first type reassign all letters, for operations of the second type let's iterate over the symbols in s from left to right and maintain the pointer to the current position in alphabet permutation. Let's move the pointer cyclically in permutation until finding the current symbol from s. And move it one more time after that. Easy to see that the answer is one plus the number of cyclic movements. Actually the answer is also the number of pairs of adjacent symbols in s that the first one is not righter than the second one in permutation. So the answer depends only on values of cntij —- the number of adjacent symbols i and j.
To make solution faster let's maintain the segment tree with matrix cnt in each node. Also we need to store in vertex the symbol in the left end of segment and in the right end. To merge two vertices in the segment tree we should simply add the values in the left and in the right sons in the tree, and update the value for the right end of the left segment and the left end of the right segment.
Complexity: O(nk2 + mk2logn).
Hello, Codeforces!
I'd like to invite you to Codeforces Round #337 (Div. 2). It'll be held on Sunday, December 27 at 14:05 MSK (Moscow time) and as usual Div. 1 participants can join out of competition. Note that round starts in the unusual time!!!
Me and Edvard Davtyan (Edvard) prepared the tasks for this Round.
Great thanks to Gleb Evstropov (GlebsHP) for helping us preparing the contest, to Maria Belova (Delinur) for translating the statements into English and to Mike Mirzayanov (MikeMirzayanov) for the great Polygon platform.
The scoring distribution will be announced later. Good luck everyone!
UPD The start time of the Round is moved on 10 minutes. Score distribution 500-1000-1500-2500-2500
UPD2 Competition completed! Thank you all! Editorial
It was easy realization problem. Let's increase the variable i from 1 to n, and inside let's increase the variable j from 1 to 2·m. On every iteration we will increase the variable j on 2. If on current iteration a[i][j] = '1' or a[i][j + 1] = '1' let's increase the answer on one.
Asymptotic behavior of this solution — O(nm).
Let's calculate the answer to every block separately from each other and multiply the answer to the previous blocks to the answer for current block.
For the block with length equals to k we can calculate the answer in the following way. Let for this block the number must be divided on x and must not starts with digit y. Then the answer for this block — the number of numbers containing exactly k digits and which divisible by x, subtract the number of numbers which have the first digit equals to y and containing exactly k digits and plus the number of numbers which have the first digit equals to y - 1 (only if y > 0) and containing exactly k digits.
Asymptotic behavior of this solution — O(n / k).
Let's sort the points by increasing x coordinate and work with sorted points array next.
Let's suppose that after optimal playing points numbered l and r (l < r) are left. It's true that the first player didn't ban any of the points numbered i l < i < r, otherwise he could change his corresponding move to point l or point r (one could prove it doesn't depend on second player optimal moves) and change the optimal answer. It turns out that all the 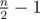 points banned by the first player have numbers outside of [l, r] segment, therefore
points banned by the first player have numbers outside of [l, r] segment, therefore 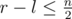 . We should notice that if the first player choosed any [l, r] for
. We should notice that if the first player choosed any [l, r] for 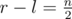 , he could always make the final points numbers located inside this segment.
, he could always make the final points numbers located inside this segment.
The second player wants to make 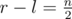 (he couldn't make less), what is equivalent if he always ban points inside final [l, r] segment (numbered l < i < r). As soon as the second player doesn't know what segment first player have chosen after every of his moves, he must detect a point which satisfies him in every first player choice. It's true number of this point is the median of set of point numbers left (the odd number) after the first player move. The number of moves of the first player left is lesser by one than moves of the second player, so the first player later could ban some points from the left and some points from the right, except three middle points. Two of it (leftmost and rightmost ones) shouldn't be banned by the second player as soon as it could increase the size of banned points from the left (or from the right), but third middle point satisfies the second player in every first player choice. This way the second player always bans the point inside final point segment.
(he couldn't make less), what is equivalent if he always ban points inside final [l, r] segment (numbered l < i < r). As soon as the second player doesn't know what segment first player have chosen after every of his moves, he must detect a point which satisfies him in every first player choice. It's true number of this point is the median of set of point numbers left (the odd number) after the first player move. The number of moves of the first player left is lesser by one than moves of the second player, so the first player later could ban some points from the left and some points from the right, except three middle points. Two of it (leftmost and rightmost ones) shouldn't be banned by the second player as soon as it could increase the size of banned points from the left (or from the right), but third middle point satisfies the second player in every first player choice. This way the second player always bans the point inside final point segment.
Thus the answer is the minimum between every of 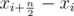 values.
values.
The main proposition to solve this problem — in the middle of every competition the sensor must be or in the top point of the wheel or in the bottom point of the wheel.
To calculate the answer we need to use binary search. If the center of the wheel moved on the distance c, then the sensor moved on the distance c + rsin(c / r), if the sensor was on the top point of the wheel in the middle, or on the distance c - rsin(c / r), if the sensor was on the bottom point of the wheel in the middle, where r — the radius of the wheel.
Asymptotic behavior of this solution —  .
.
Let's find the centers of every rectangle and multiple them of 2 (to make all coordinates integers).Then we need to by the rectangle door, which contains all dots, but the lengths of the sides of this door must be rounded up to the nearest integers.
Now, let's delete the magnets from the door one by one, gradually the door will decrease. Obviously every time optimal to delete only dots, which owned to the sides of the rectangle. Let's brute 4k ways, how we will do delete the magnets. We will do it with helps of recursion, every time we will delete point with minimum or maximum value of the coordinates. If we will store 4 arrays (or 2 deques) we can do it with asymptotic O(1). Such a solution works O(4k).
It can be easily shown that this algorithm delete always some number of the leftmost, rightmost, uppermost and lowermost points. So we can brute how k will distributed between this values and we can model the deleting with helps of 4 arrays. This solution has asymptotic behavior O(k4).
To calculate the answer on every query let's use the formula 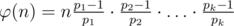 , where p1, p2, ..., pk — all prime numbers which divided n. We make all calculations by the module 109 + 7
, where p1, p2, ..., pk — all prime numbers which divided n. We make all calculations by the module 109 + 7
Let's suppose that we solving problem for fix left end l of the range. Every query now is a query on the prefix of the array. Then in formula for every prime p we need to know only about the leftmost position of it. Let's convert the query in the query of the multiple on the prefix: at first init Fenwick tree with ones, then make the multiplication in points l, l + 1, ..., n with value of the elements al, al + 1, ..., an. For every leftmost positions of prime p make in position i the multiplication in point i on the 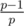 . This prepare can be done with asymptotic
. This prepare can be done with asymptotic 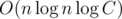 , where C — the maximum value of the element (this logarithm — the number of prime divisors of some ai).
, where C — the maximum value of the element (this logarithm — the number of prime divisors of some ai).
We interest in all leftmost ends, because of that let's know how to go from the one end to the other. Let we know all about the end l — how to update the end l + 1? Let's make the multiplication in the Fenwick tree in the point l on the value al - 1. Also we are not interesting in all prime numbers inside al, so let's make the multiplications in point l on the all values 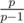 . But every of this prime numbers can have other entries which now becoming the leftmost. Add them with the multiplication which described above. With helps of sort the transition between leftmost ends can be done in
. But every of this prime numbers can have other entries which now becoming the leftmost. Add them with the multiplication which described above. With helps of sort the transition between leftmost ends can be done in 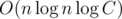 .
.
To answer to the queries we need to sort them in correct order (or add them in the dynamic array), and to the get the answer to the query we will make  iterations. So total asymptotic behavior of solution is
iterations. So total asymptotic behavior of solution is 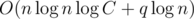 iterations and
iterations and 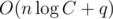 additional memory.
additional memory.
Let's describe the greedy algorithm, which allows to solve the problem for every k > 2 for every string S.
Let's think, that we always reverse some prefix of the string S (may be with length equals to one). Because we want to minimize lexicographically the string it is easy to confirm that we will reverse such a prefixes, which prefix (after reversing) is equals to the minimal lexicographically suffix of the reverse string S (let it be Sr) — this is prefix, which length equals to the length of the minimum suffix Sr (the reverse operation of the prefix S equals to change it with suffix Sr).
Let the lexicographically minimal suffix of the string Sr is s. It can be shown, that there are no 2 entries s in Sr which intersects, because of that the string s will be with period and minimal suffix will with less length. So, the string Sr looks like tpsaptp - 1sap - 1tp - 2... t1sa1, where sx means the concatenation of the string s x times, a1, a2, ..., ap — integers, and the strings t1, t2, ..., tp — some non-empty (exclude may be tp) strings, which do not contain the s inside.
If we reverse some needed prefix of the string s, we will go to the string S', and the minimal suffix s' of the reversing string S'r can't be lexicographically less than s, because of that we need to make s' equals to s. It will helps us to increase prefix which look like sb in the answer (and we will can minimize it too). it is easy to show, that maximum b, which we can get equals to a1 in case p = 1 и 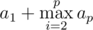 (in case if p \geq 2$). After such operations the prefix of the answer will looks like sa1saitisai - 1... sa2t2. Because t_{i} — non-empty strings we can not to increase the number of concatenations s in the prefix of the answer. The reversing of the second prefix (sai...) can be done because k > 2.
(in case if p \geq 2$). After such operations the prefix of the answer will looks like sa1saitisai - 1... sa2t2. Because t_{i} — non-empty strings we can not to increase the number of concatenations s in the prefix of the answer. The reversing of the second prefix (sai...) can be done because k > 2.
From the information described above we know that if k > 2 for lost string we need always reverse prefix, which after reversing is equals to the suffix of the string Sr which looks like sa1. To find this suffix every time, we need only once to build Lindon decomposition (with helps of Duval's algorithm) of the reverse string and carefully unite the equals strings. Only one case is lost — prefix of the lost string does not need to be reverse — we can make the concatenation of the consecutive reverse prefixes with length equals to 1.
Because for k = 1 the problem is very easy, we need to solve it for k = 2 — cut the string on the two pieces (prefix and suffix) and some way of their reverse. The case when nothing reverse is not interesting, let's look on other cases:
Prefix do not reverse. In this case always reversing suffix. Two variants of the string with reverse suffix we can compare with O(1) with helps of z-function of the string Sr#S.
Prefix reverse. To solve this case we can use approvals from the editorial of the problem F Yandex.Algorithm 2015 Round 2.2 which was written by GlebsHP and check only 2 ways of reversing prefix. We need for them to brute the reverse of suffixes.
It is only need in the end to choose from 2 cases better answer. Asymptotic behavior of the solution is O(|s|).
Hello, Codeforces!
I'd like to invite you to Codeforces Round #322 (Div. 2). It'll be held on Monday, September 28 at 12:00 MSK and as usual Div. 1 participants can join out of competition. Note that round starts in the unusual time!
This round is held on the tasks of the school stage All-Russian Olympiad of Informatics 2015/2016 year in city Saratov. They were prepared by me and recently returned from army Edvard Davtyan (Edvard).
Great thanks to Maxim Akhmedov (Zlobober) for helping me preparing the contest, to Maria Belova (Delinur) for translating the statements into English, to Mike Mirzayanov (MikeMirzayanov) for the great Polygon platform and ideas of some problems and to Vladimir Petrov (vovuh) for writing solutions.
It will be a little unusual round — you will be given six problems and two hours to solve them. The scoring distribution will be announced later. Good luck everyone!
UPD The scoring distribution today will be 500-1000-1500-2000-3000-3000.
UPD2 Editorial
UPD3 Congratulations to the winners!
581A — Vasya the Hipster
The first number in answer (number of days which Vasya can dress fashionably) is min(a, b) because every from this day he will dress one red sock and one blue sock.
After this Vasya will have either only red socks or only blue socks or socks do not remain at all. Because of that the second number in answer is max((a - min(a, b)) / 2, (b - min(a, b)) / 2).
Asymptotic behavior of this solution — O(1).
581B — Luxurious Houses
This problem can be solved in the following way. Let's iterate on given array from the right to the left and will store in variable maxH the maximal height if house which we have already considered.Then the answer to house number i is number max(0, maxH + 1 - hi), where hi number of floors in house number i.
Asymptotic behavior of this solution — O(n), where n — number of houses.
581C — Developing Skills
This problem can be solved in many ways. Let's consider the most intuitive way that fits in the given time.
In the beginning we need to sort given array in the following way — from two numbers to the left should be the number to which must be added fewer units of improvements to make it a multiple of 10. You must add at least one unit of energy to every of this numbers. For example, if given array is {45, 30, 87, 26} after the sort the array must be equal to {87, 26, 45, 30}.
Now we iterate on the sorted array for i from 1 to n. Let's cur = 10 - (aimod10). If cur ≤ k assign ai = ai + cur and from k subtract cur else if cur > k break from cycle.
The next step is to iterate on array in the same way.
Now we need only to calculate answer ans — we iterate on array for i from 1 to n and assign ans = ans + (ai / 10).
Asymptotic behavior of this solution — O(n * log(n)) where n is the number of hero skills.
581D — Three Logos
This problem can be solved in many ways, let's consider one of them.
The first step is to calculate sum of squares s of given rectangles. Then the side of a answer square is sqrt(s). If sqrt(s) is not integer print -1. Else we need to make the following.
We brute the order in which we will add given rectangles in the answer square (we can do it with help of next_permutation()) and for every order we brute will we rotate current rectangle on 90 degrees or not (we can do it with help of bit masks). In the beginning on every iteration the answer square c in which we add the rectangles is empty.
For every rectangle, which we add to the answer square we make the following — we need to find the uppermost and leftmost empty cell free in answer square c (recall that we also brute will we rotate the current rectangle on 90 degrees or not). Now we try to impose current rectangle in the answer square c and the top left corner must coinside with the cell free. If current rectangle fully placed in the answer square c and does not intersect with the some rectangle which has already been added, we need to fill by the required letter appropriate cells in the answer square c.
If no one of the conditions did not disrupted after we added all three rectangles and all answer square c is fully filled by letters we found answer and we neeed only to print the answer square c.
Else if we did not find answer after all iterations on the rectangles — print -1.
For random number of the rectangles k asymptotic behavior — O(k! * 2k * s) where s — the sum of squares of the given rectangles.
Also this problem with 3 rectangles can be solved with the analysis of the cases with asymptotic O(s) where s — the sum of squares of given rectangles.
581E — Kojiro and Furrari
Let's f — the position of start, and e — the position of finish. For convenience of implementation we add the gas-station in point e with type equals to 3.
Note: there is never a sense go to the left of the starting point because we already stand with a full tank of the besr petrol. It is correct for every gas-station in which we can appear (if in optimal answer we must go to the left in some gas-station pv, why not throw out all the way from pv to current gas-station v and back and after that the answer will be better). Now let's say about algorithm when we are in some gas-station v.
The first case: on distance no more than s there is the gas-station with quality of gasoline not worse, than in the current gas-station. Now we fix nearest from them nv (nearest to the right because go to the left as we understand makes no sense). In that case we refuel in such a way to can reach nv and go to nv.
The second case: from the current gas-station we can reach only gas-station with the worst quality (the type of the current gas-station can be 2 or 3). If we are in the gas-station of type 2 we need to refuel on maximum possiblevalue and go in the last achievable gas-station. If we are in the gas-station with type 3, we need to go in the farthest gas-station with type 2, but if there is not such gas-station we need to go to the farthest gas-station with type 1. This reasoning are correct because we first need to minimze the count of fuel with type 1, and the second to minimize the count of fuel with type 2.
This basic reasoning necessary to solve the problem. The next step — calc dynamic on all suffixes i of gas-stations — the answer to the problem if we start from the gas-station i with empty tank. We need to make updates, considering the above cases. For update the dynamic in v we need to take the value of dynamic in nv and make update in addiction of the case. If the case is equals to 1, we need to add to appropriate value the distance d from v to nv. If this case is equals to 2 and we are in the gas-station with type equals to 2 we need to add s to the second value of answer, and from the first value we need to substract s–d. If it is the case number 2 and we are in the gas-station with type equals to 3, we need to substract from the value, which determined by the type of the gas-station nv, s–d.
Now to answer on specific query of the starting position we nned to find the first gas-station which is to the right of the startiong position, make one update and take the value of dynamic, which already calculated, and recalculate this value in accordance with the above.
Asymptotic behavior — O(n logn) or O(n) in case how we find position in the list of gas-stations (the first in case of binary search, the second in case of two pointers).
To this solution we need O(n) memory.
581F — Zublicanes and Mumocrates
Let the number of leavs in tree (vertices with degree 1) is equal to c. It said in statement that c is even. If in given graph only 2 vertices the answer is equal to 1. Else we have vertex in graph which do not a leaf — we hang the three on this vertex.
Now we need to count 2 dynamics. The first z1[v][cnt][col] — the least amount of colored edges in the subtree rooted at the vertex v, if vertex v already painted in color col (col equals to 0 or to 1), and among the top of the leaves of the subtree v must be exactly cnt vertices with color 0. If we are in the leaf, it is easy to count this value. If we are not in the leaf — we count value with help of dynamic z1[v][cnt][col]: = z2[s][cnt][col], where s — the first child int the adjacency list of vertex v.
We need the second dynamic z2[s][cnt][col] to spread cnt leaves with color 0 among subtrees of childs of vertex v. To calc z2[s][cnt][col] we brute the color of child s — ncol and the number of childs i with color 0, which will be locate in subtree of vertex s and calc the value in the following way — z2[s][cnt][col] = min(z2[s][cnt][col], z2[ns][cnt–a][col] + z1[s][a][ncol] + (ncol! = col)), where ns — the next child of vertex v after the child s. Note, that it is senselessly to take a more than the number of leaves in the subtree s and to take more than the number of vertices in subtree — sizes (because in that case it will not be enough leaves for painting).
The upper bound of asymptotic for such dynamics O(n3). We show that in fact it works with asymptotic O(n2). Let's count the number of updates: 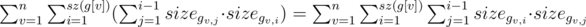 . Note, that every pair of vertices (x, y) appears in the last sum (x, y) exactly once when v = lca(x, y). So we have no more than O(n2) updates.
. Note, that every pair of vertices (x, y) appears in the last sum (x, y) exactly once when v = lca(x, y). So we have no more than O(n2) updates.
Asymptotic behavior of this solution: O(n2).
Hello, Codeforces!
Previously, my contribution to the development of Codeforces was limited only by rounds preparation (Codeforces Round 288 (Div. 2), Codeforces Round 293 (Div. 2), Codeforces Round 297 (Div. 2)). But a month ago, I joined the wonderful Codeforces team led by Mike Mirzayanov (MikeMirzayanov). Traditionally, to understand all the niceties of this project, my work begun from Polygon system. I would like to tell you about its changes.
Polygon is a system for the preparation of programming problems. All Codeforces rounds and many other olympiads prepared in Polygon. Everyone at any time can use this system.
To edit the files in Polygon now used Ace Editor. It has a nice looking syntax highlighting and autocompletion (you have to press Ctrl + Space). Soon planned to implement this editor in Codeforces.
Hello, Codeforces!
I'd like to invite you to Codeforces Round #311 (Div. 2). It'll be held on Tuesday, June 30 at 18:00 MSK and as usual Div. 1 participants can join out of competition. Note that round starts in the unusual time!
Great thanks to Maxim Akhmedov (Zlobober) for helping me preparing the contest, to Maria Belova (Delinur) for translating the statements into English, to Mike Mirzayanov (MikeMirzayanov) for the great Polygon platform and ideas of some problems and to my friends Ilya Los (IlyaLos) and Danil Sagunov (danilka.pro) for writing solutions.
The scoring distribution will be announced later. Good luck everyone!
UPD The scoring distribution will be standard today 500-1000-1500-2000-2500.
UPD2 Competition completed! Thank you all!
UPD3 You can find editorial here.
557A — Ilya and Diplomas
This problem can be solved in the different ways. We consider one of them — parsing cases.
If max1 + min2 + min3 ≤ n then the optimal solution is (n - min2 - min3, min2, min3).
Else if max1 + max2 + min3 ≤ n then the optimal solution is (max1, n - max1 - min3, min3).
Else the optimal solution is (max1, max2, n - max1 - max2).
This solution is correct because of statement. It is guaranteed that min1 + min2 + min3 ≤ n ≤ max1 + max2 + max3.
Asymptotic behavior of this solution — O(1).
557B — Pasha and Tea
This problem can be solved in different ways too. We consider the simplest solution whici fits in the given restrictions.
At first we sort all cups in non-decreasing order of their volumes. Due to reasons of greedy it is correct thatsorted cups with numbers from 1 to n will be given to girls and cups with numbers from n + 1 to 2 * n will be given to boys.
Now we need to use binary search and iterate on volume of tea which will be poured for every girl. Let on current iteration (lf + rg) / 2 = mid. Then if for i from 1 to n it is correct that mid ≤ ai and for i from n + 1 to 2 * n it is correct that 2 * mid ≤ ai then we need to make lf = mid. Else we need to make rg = mid.
Asymptotic behavior of this solution — O(n * log(n)) where n — count of cups.
557C — Arthur and Table
This problem can be solved as follows. At first we need to sort all legs in non-descending order of their length. Also we need to use array cnt[].
Let iterate on length of legs (which will stand table) from the least. Let this lenght is equals to maxlen. Count of units of energy which we need for this we will store in variable cur.
Obviously that we must unscrew all legs with lenght more than maxlen. For calculate count of units of energy for doing it we can use array with suffix sums, for exapmle. Then we add this value to cur.
If count of legs with length maxlen is not strictly greater than the number of the remaining legs then we need to unscrew some count of legs with length less than maxlen. For this we can use array cnt[]. In cnt[i] we will store count of legs with difficulty of unscrew equals to i. In this array will store information about legs which already viewed.
We will iterate on difficulty of unscrew from one and unscrew legs with this difficulties (and add this difficulties to variable cur) while count of legs with length maxlen will not be strictly greater than the number of the remaining legs.
When it happens we need to update answer with variable cur.
Asymptotic behavior of this solution — O(n * d), where n — count of legs and d — difference between maximal and minimal units of energy which needed to unscrew some legs.
557D — Vitaliy and Cycle
To solve this problem we can use dfs which will check every connected component of graph on bipartite. It is clearly that count of edges which we need to add in graph to get the odd cycle is no more than three.
Answer to this problem is three if count of edges in graph is zero. Then the number of ways to add three edges in graph to make odd cycle is equals to n * (n - 1) * (n - 2) / 6 where n — count of vertices in graph.
Answer to this problem is two if there is no connected component with number of vertices more than two. Then the number of ways to add two edges in graph to make odd cycle is equals to m * (n - 2) where m — number of edges in graph.
Now we have one case when there is at least one connected component with number of vertices more than two. Now we need to use dfs and try to split every component in two part. If for some component we can't do it that means that graph already has odd cycle and we need to print "0 1" and we can now finish our algorithm.
If all connected components in graph are bipartite then we need to iterate on them. Let cnt1 is the count of vertices in one part of current component and cnt2 — count of vertices in the other part. If number of vertices in this component more than two we need to add to answer cnt1 * (cnt1 - 1) / 2 and cnt2 * (cnt2 - 1) / 2.
Asymptotic behavior of this solution — O(n + m), where n — number of vertices in graph and m — number of edges.
557E — Anya and Half-palindrome
This problem can be solved with help of dynamic programming.
At first we calculate matrix good[][]. In good[i][j] we put true, if substring from position i to position j half-palindrome. Else we put in good[i][j]false. We can do it with iterating on "middle" of half-palindrome and expanding it to the left and to the right. There are 4 cases of "middle" but we omit it because they are simple enough.
Now we need to use Trie and we will put in it suffixes of given string. Also we will store array cnt[]. In cnt[v] we will store number of half-palindromes which ends in vertex v of our Trie. Let now we put in tree suffix which starts in position i, current symbol of string which we put is in position j and we go in vertex v of out Trie. Then if good[i][j] = true we add one to cnt[v].
Now with help of dfs let calculate for every vertex sum[v] — sum of numbers which stored in array cnt[] for vertex v and for vertices in all subtrees of vertex v.
It is left only to restore answer. Start from root of our Trie. We will store answer in variable ans. In variable k store number of required substring. Let now we in vertex v, by letter 'a' we can go in vertex toa and by letter 'b' — in vertex tob.
Then if sum[toa] ≤ k we make ans + = 'a' and go in vertex toa of our Trie. Else we need to make as follows: k — = sum[toa], ans + = 'b' and go in vertex tob of our Trie.
When k will be ≤ 0 print resulting string ans and finish algorithm.
Asymptotic behavior of this solution — O(szalph * n2) where szalph — size of input alphabet (in this problem it equals to two) and n — length of given string.
Hello, Codeforces!
I'd like to invite you to Codeforces Round #297 (Div. 2). It'll be held on Thursday, March 26 at 19:30 MSK and as usual Div. 1 participants can join out of competition.
Great thanks to Maxim Akhmedov (Zlobober) for helping me preparing the contest, to Maria Belova (Delinur) for translating the statements into English, to Mike Mirzayanov (MikeMirzayanov) for the great Polygon platform and ideas of some problems and to my old friends Pavel Kholkin (HolkinPV), Ilya Los (IlyaLos), Vitaliy Kudasov (kuviman) and Arthur Svechnikov (ikar) for writing solutions.
The scoring distribution will be announced later. Good luck everyone!
UPD The scoring is smooth dynamic (with steps of 250 points). More information about this can be found here. Tasks will be arranged in order of ascending supposed difficulty.
UPD2 Competition completed! Thank you all!
UPD3 You can find editorial here.
UPD4 Congratulations to the winners!
525A — Vitaliy and Patty
To solve this problem we need to use array cnt[]. In this array we will store number of keys of every type, which we already found in rooms, but didn't use. Answer will store in variable ans.
Now, we iterate on string. If current element of string si is lowercase letter (key), we make cnt[si]++. Else if current element of string si uppercase letter (door) and cnt[tolower(si)] > 0, we make cnt[tolower(si)]--, else we make ans++. It remains only to print ans.
Asymptotic behavior of this solution — O(|s|), where |s| — length of string s.
525B — Pasha and String
At first we need to understand next fact — it doesn't matter in wich order make reverses, answer will be the same for all orders.
Let's numerate elements of string from one. To solve given problem we need to count how many reverses will begin in every position of string. Then we need to count array sum[]. In sum[i] we need to store count of reverses of substrings, which begin in positions which not exceeding i.
Now iterate for i from 1 to n / 2 and if sum[i] is odd swap si and sn - i + 1. After that it remains only to print string s.
Asymptotic behavior of this solution — O(n + m), where n — length of string s, m — count of reverses.
525C — Ilya and Sticks
This problem can be solved with help of greedy. At first count array cnt[]. In cnt[i] will store how many sticks with length i we have.
Now iterate for len from maximal length of sticks to minimal. If cnt[len] is odd and we have sticks with length len - 1 (that is cnt[len - 1] > 0), make cnt[len]-- and cnt[len - 1]++. If cnt[len] is odd and we have no sticks with length len - 1 (that is cnt[len - 1] = 0), make cnt[len]--.
In this way we properly done all sawing which we need and guaranteed that all cnt[len] is even. After that iterate similary on length of sticks and greedily merge pairs from 2 sticks with the same length in fours. It will be length of sides of sought-for rectangles, left only summarize their squares in answer. In the end can left 2 sticks without pair, we must not consider them in answer.
For example, if cnt[5] = 6, cnt[4] = 4, cnt[2] = 4, we need to merge this sticks in following way — (5, 5, 5, 5), (5, 5, 4, 4), (4, 4, 2, 2). Two sticks with length 2 are left, we must not count them.
Asymptotic behavior of this solution — O(n + maxlen - minlen), where n — count of sticks, maxlen — maximal length of stick, minlen — minimal length of stick.
525D — Arthur and Walls
To solve this problem we need to observe next fact. If in some square whith size 2 × 2 in given matrix there is exactly one asterisk, we must change it on dot. That is if in matrix from dots and asterisks is not square 2 × 2 in which exactly one asterisk and three dots, then all maximum size of the area from dots connected by sides represent rectangles.
Now solve the problem with help of bfs and this fact. Iterate on all asterisks in given matrix and if only this asterisk contains in some 2 × 2 square, change this asterisk on dot and put this position in queue. Than we need to write standart bfs, in which we will change asterisks on dots in all come out 2 × 2 squares with exactly one asterisk.
Asymptotic behavior of this solution — O(n * m), where n and m sizes of given matrix.
525E — Anya and Cubes
To solve this problem we need to use meet-in-the-middle. At first sort given array in increasing order and divide it in two parts. In first part must be first n / 2 elements, in second part — other.
Iterate all submasks of all masks of elements from first part. That is iterate which cubes from first part we take and on which from them we paste exclamation marks. In this way we iterated all possible sums, which we can get with cubes from first part. Let for current submask we get sum sum_lf and use tlf exclamation marks. To store all such sums we use associative arrays map < long long > cnt[k + 1], where k — count of exclamation marks which we have in the beginning.
After that similary iterate all submasks of all masks of elements from second part. Let for current submask sum is sumrg and number of used exclamation marks is trg. Then from first part we need to get sum (s - sumrg) and we can use only (k - trg) exclamation marks, where s — sum which we must get by condition of the problem. Then iterate how many exclamation marks we will use in first part (let it be variable cur) and increase answer on cnt[cur][s - sumrg]. To accelerate our programm we may increase answer only if cnt[cur].count(s - sumrg) = true.
For submasks in iterate we can cut off iteration on current sum for submask (it must be less or equal to given s) and on current count of exclamation marks (it must be less or equal to given k). Also we should not paste exclamation marks on cubecs with numbers larger than 18, because 19! more than 1016 — maximal value of s.
Asymptotic behavior of this solution — O(3((n + 1) / 2) * log(maxcnt) * k), where n — count of cubes, maxcnt — maximal size of associative array, k — count of exclamation marks.
517A — Vitaly and Strings
To solve this problem we can, for example, find string next, which lexicographically next to string s and check that string next is lexicographically less than string t. If string next is lexicographically smaller than string t, print string next and finish algorithm. If string next is equal to string t print No such string.
To find string next, which lexicographically next to string s, at first we need to find maximal suffix of string s, consisting from letters 'z', change all letters 'z' in this suffix on letters 'a', and then letter before this suffix increase on one. I.e. if before suffix was letter, for example, 'd', we need to change it on letter 'e'.
Asymptotic behavior of this solution — O(|s|), where |s| — length of string s.
517B — Tanya and Postcard
To solve this problem at first will count array cnt[], where cnt[c] — how many times letter c found in string t. We will count two numbers ans1 and ans2 — how many times Tanya will shouts joyfully YAY! and how many times Tanya will says WHOOPS.
Let's iterate on string s and if cnt[s[i]] > 0, then increase ans1 on one and decrease cnt[s[i]] on one.
Then let's again iterate on string s. Let c is letter which equal to s[i],but in the opposite case for it. I. e. if s[i] = 'w', then c = 'W'. Now, if cnt[c] > 0, then increase ans2 on one and decrease cnt[с] on one.
Now, print two numbers — ans1 and ans2.
Asymptotic behavior of this solution — O(|s| + |t|), where |s| — length of string s and |t| — length of string t.
517C — Anya and Smartphone
To solve this problem we will store two arrays — a[] and pos[]. In array a[] will store current order of icons, i. e. in a[i] store number of application, icon which stay on position i. In array pos[] will store on which place in list stays icons, i. e. in pos[i] store in which position of array a[] stay icon of application number i. We will count answer in variable ans.
Let's iterate on applications which we need to open. Let current application has number num. Then to ans we need add (pos[num] / k + 1). Now, if icon of application number num doesn't stay on first position in list of applications, we make the following — swap a[pos[num]] and a[pos[num] - 1] and update values in array pos[] for indexes of two icons which numbers a[pos[num]] and a[pos[num] - 1] .
Asymptotic behavior of this solution — O(n + m), where n — number of applications, m — number of requests to start applications.
517D — Ilya and Escalator
To solve this problem let's use dynamic programming. We will store two-dimensional array z[][] with type double. In z[i][j] will store the likelihood that after i seconds j people are on escalator.
In dynamic will be following transitions. If j = n, i. e. all n people already on escalator then we make transition z[i + 1][j] + = z[i][j]. Else, or person number j go to escalator in i + 1 second, i. e. z[i + 1][j + 1] + = z[i][j] * p, or person number j stays on his place, i. e. z[i + 1][j] + = z[i][j] * (1 – p).
Now we need to count answer — it is sum on j from 0 to n inclusive z[t][j] * j.
Asymptotic behavior of this solution — O(t * n), where t — on which moment we must count answer, n — how many people stay before escalator in the beginning.
517E — Arthur and Questions
At first let's take two sums a1 + a2 + ... + ak and a2 + a3 + ... + ak + 1. It is correct that a1 + a2 + ... + ak < a2 + a3 + ... + ak + 1. If move from right to left all elements apart from ak + 1, all of them will reduce and will left only a1 < ak + 1. If write further all sums we will obtain that sequence disintegrate on k disjoint chains: a1 < ak + 1 < a2k + 1 < a3k + 1..., a2 < ak + 2 < a2k + 2 < a3k + 2..., ..., ak < a2k < a3k....
We will solve the problem for every chain separately. Let's iterate on first chain and find all pair of indexes i, j (i < j), that a[i] and a[j] are numbers (not questions) in given sequence, and for all k from i + 1 to j - 1 in a[k] stay questions. All this questions we need to change on numbers so does not violate the terms of the increase and minimize sum of absolute values of this numbers.
Between indexes i and j stay j - i - 1 questions, we can change them on a[j] - a[i] - 1 numbers. If j - i - 1 > a[j] - a[i] - 1, then we need to print Incorrect sequence and finish algorithm. Else we need to change all this questions to numbers in greedy way.
Here we have several cases. Will review one case when a[i] > = 0 and a[j] > = 0. Let current chain (3, ?, ?, ?, 9), i = 1, j = 5. We need to change questions on numbers in the following way — (3, 4, 5, 6, 9). In other cases (when a[i] < = 0, a[j] < = 0 and when a[i] < = 0, a[j] > = 0) we need to use greedy similary to first so does not violate the terms of the increase and minimize sum of absolute values of this numbers.
Asymptotic behavior of this solution — O(n), where n — count of elements in given sequence.
517F — Pasha and Pipe
At first let's count two two-dimensional arrays of prefix sums sumv[][] and sumg[][]. In sumv[i][j] store how many grids are in column j beginning from row 1 to row i. In sumg[i][j] store how many grid are in row i beginning from column 1 to column j.
Let's count ans0 — how many pipes without bending we can pave. Count how many vertical pipes — we can pave. Iterate on j from 2 to m — 1 and, if sumg[n][j] — sumg[n][0] = 0 (i. e. in this column zero grids), increase ans0 on one. Similary count number of horizontal pipes.
Let's count ans1 — how many pipes with 1 bending we can pave. We need to brute cell, in which will bending. There are four cases. Let's consider first case, others we can count similary. This case — pipe begin in left column, go to current cell in brute and then go to top row. If brute cell in row i and column j then to ans1 we need to add one, if (sumg[i][j] — sumg[i][0]) + (sumv[i][j] — sumv[0][j]) = 0.
Let's count ans2 — how many pipes with 2 bendings we can pave. Let's count how many tunes begin from top row and end in top or bottom row and add this number to ans2. Then rotate our matrix three times on 90 degrees and after every rotate add to ans2 count of pipes, which begin from top row and end in top or bottom row. Then we need divide ans2 to 2, because every pipe will count twice.
How we can count to current matrix how many pipes begin from top row and end in top or bottom row? Let's count four two-dimension arrays lf[][], rg[][], sumUp[][], sumDown[][]. If i — number of row, j — number of column of current cell, then in position (i, lf[i][j]) in matrix are nearest from left grid for cell (i, j), and in position (i, rg[i][j]) in matrix are nearest from right grid for cell (i, j). sumUp[i][j] — how many columns without grids are in submatrix from (1, 1) to (i, j) of given matrix. sumDown[i][j] — how many columns without grids are in submatrix from (i, 1) to (n, j) of given matrix. Then let's brute cell in which will be the first bending of pipe (pipe goes from top row and in this cell turned to left or to right), check, that in column j above this cell 0 grids, with help of arrays lf and rg find out as far as pipe can go to left or to right and with help of arrays sumUp and sumDown carefully update answer.
Now print number ans1 + ans2 + ans3.
Asymptotic behavior of this solution — O(n * m * const), where n — hoew many rows in given matrix, m — how many columns in given matrix, const takes different values depending on the implementation, in solution from editorial const = 10.
Hello, Codeforces!
I'd like to invite you to Codeforces Round #293 (Div. 2). It will be held on Tuesday, February 24 at 19:30 MSK and as usual Div. 1 participants are invited to join out of competition.
Great thanks to Maxim Akhmedov (Zlobober) for helping me preparing the contest, to Maria Belova (Delinur) for translating the statements into English, to Mike Mirzayanov (MikeMirzayanov) for the great Polygon platform and ideas of some problems and to my dear friends Pavel Kholkin (HolkinPV), Arthur Svechnikov (ikar) and Vitaliy Kudasov (kuviman) for writing solutions.
It will be a little unusual round — you will be given six problems and two and half hours to solve them.
UPD Score distribution will be 500-1000-1500-2000-2500-2500. Good luck everyone!
UPD2 Competition completed! Thank you all!
UPD3 You can find editorial here.
UPD4 Congratulations to the winners!
508A — Pasha and Pixels
To solve this problem let's create matrix with type bool and dimensions n on m. Cell (x, y) of this matrix is true — if this cell painted in black color.
Let on move number k Pasha paints pixel in position (i, j). Then game ending on this move, if square 2 × 2 formed from black cells appears, and cell (i, j) will upper-left, upper-right, bottom-left or bottom-right of this squares. Only this squares we need to check on current move. If we haven't such squares after k moves, print 0. Asymptotic behavior of this solution — O(k), where k — number of moves.
508B — Anton and currency you all know
Because of specified number is odd (that mean that last digit of this number is odd) we need to swap last digit with some even digit. How to maximize number after this swap?
If number consists only from odd digits print - 1.
Else, we need to find first even digit, which less than last digit if we will iterate from most significant digit. If we find such digit — swap it with last digit and we have an answer.
Else, we need to find first even digit, which more than last digit if we will iterate from less significant digit. If we find such digit — swap it with last digit and we have an answer.
Asymptotic behavior of this solution — O(n), where n — count of digits in specified number.
508C — Anya and Ghosts
This problem can be solved with help of greedy algorithm. Let's iterate on moments when ghosts will appears.
We need to use use array, in wich we will mark moments of time, in wich we lighted candles (for example, put in corresponding positions 1). Than for every new ghost will count how many candles lights in time of his visit from our array.
If ghost appears in moment of time wi, iterate on out array from wi - 1 to wi - t, where t — count of seconds, which candle burns, and count the number of ones. If this count is not less than r, continue iterating on ghosts. Else, iterate on our array from wi - 1 to wi - t, and, if in current second candle didn't lighted — make it, and put in this position in array 1. We need to do such operation, while count of ones in this section of our array will not be equals to r. If we can't do this fore some ghost, we can print - 1.
Answer to this problem — count of ones in our array. Asymptotic behavior of this solution — O(mt), where m — count of ghosts, t — the duration of a candle's burning.
508D — Tanya and Password
At first, let's convert data from input in directed graph. Vertexes in this graph will all strings with length equals to 2 and consisting of uppercase and lowercase letters of the latin alphabet. For all 3-letters strings from input — si's, let's add edge from vertex si[0]si[1] to si[1]si[2].
Now we need to find in this graph Euler path. For this we can use Fleury's algorithm. It is worth noting, that Euler path consists, if count of vertexes, in wich in-degree and out-degree differs by one, less then 3, and in-degree and out-degree of others vertexes — even. If we can't find Euler path — print NO. Asymptotic behavior of this solution — O(m), where m — count of different 3-letters strings from input. It equals to number of edges in graphs.
508E — Arthur and Brackets
This problem can be solved with help of dynamic dynamic programming. Let's create squre matrix Z with sizes n × n, where n — count of open brackets in sequence. Main hint — if open bracket is in position l, and corresponding for her close bracket — in position r, than from position l + 1 to position r - 1 must stay a regular bracket sequence.
In array Z first parametr lf — number of open bracket, second parametr rg — number of last open bracket, which can be in a regular bracket sequence, which will exists between open bracket with number lf and corresponding for it close bracket.
Z[lf][rg] = true if it is possible to construct such sequence. Otherwise Z[lf][rg] = false.
For current lf and rg let's iterate on cnt — how many open brackets and corresponding them close brackets in a regular bracket sequence will stay between open bracket number lf and corresponding for it close bracket. If this count falls in the given interval for open bracket lf, recurcively run dynamic from two segments — (lf + 1, lf + cnt) and (lf + cnt + 1, rg).
If for both segments we can construct regular bracket sequences, appropriate to data-in from input, put in Z[lf][rg] value true. To restore answer, we must move from segment (lf, rg) in segments (lf + 1, lf + cnt) and (lf + cnt + 1, rg), if for both this segments we can construct regular bracket sequences and recursively restore asnwer. If Z[0][n - 1] equals to false, print IMPOSSIBLE. Asymptotic behavior of this solution — O(n3).
UPD This problem can be solved with help of griddy algorithm. Asymptotic behavior of this solution — O(n). Here is example of such solution, participant matrix.
| Name |
|---|










