| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 164 |
| 1 | maomao90 | 164 |
| 3 | Um_nik | 163 |
| 4 | atcoder_official | 160 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 8 | Dominater069 | 154 |
| 8 | nor | 154 |
Всем привет!
Недавно задумался как решить такую задачу: Есть корень дерева, за каждый ход игрок может у любого листа дерева создать либо левого потомка (с вероятностью p), либо правого (с вероятностью 1 - p). Какого математическое ожидание высоты дерева после n ходов игрока?
UPD: Лист выбирается равновероятно.
Лист -- эта вершина с количеством потомков меньше 2.
Лист выбирается равновероятно?
Да
Можешь сформулировать условие по-точнее. Что есть лист в данной задаче? Вершина, у которой строго меньше 2-ух потомков? я правильно понял? Интересно было бы узнать откуда задача.
Кстати (предположение) при равновероятном выборе (не полной, без 2-ух потомков) вешины и добавлении потомка — ответ на задачу не должен зависеть от того левого или правого мы добавляем.
Вообще-то вроде вы правы. Задача просто придуманная во время неинтересной пары. Насчет выбора листа -- да, равновероятно.
В таком случае, как я понимаю интерес представляет следующая задача: Сначала мы (в зависимости от вероятности p) выбираем "левую" или "правую" вершину мы будем добавлять, а затем среди всех возможных вершин, к которым можно прицепить "левого" или "правого" потомка (в зависимости от сделанного ранее выбора) выбираем равновероятно.
В такой формулировке по крайней мере есть явная зависомость от p.
p = 0 или 1 : ans = n;
p = 0.5 :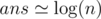
;