Привет всем! Есть такая задача: Необходимо найти сумму Минковского для двух почти выпуклых многоугольников, где почти выпуклый многоугольник — многоугольник, полученный из выпуклого многоугольника путем замены некоторых ребер дугами с углом от 0 до PI радиан. (Сумма Минковского для двух многоугольников (a), (b) равна многоугольнику, полученному путем прибавления каждой точки многоугольника (a) к каждой точке многоугольника b.)
В идеале асимптотика O(n + m), где n — количество вершин первого почти выпуклого многоугольника, m — количество вершин второго почти выпуклого многоугольника.
Для просто выпуклых многоугольников сумма Минковского тривиальна, но задача с заменой некоторых ребер дугами меня ставит в тупик. Прошу помочь советом/идеей/какой-либо литературой/решением. Заранее благодарен!
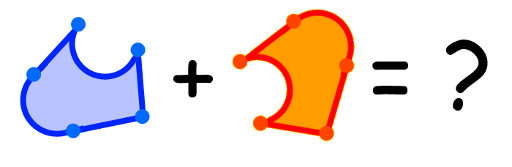











Задача весьма интересная. А откуда Вы ее взяли?
UPD. Гуглинг по запросу "сумма Минковского для невыпуклых многоугольников" дает ссылку на эту статью. Этой статьи уже достаточно, чтобы построить рабочий алгоритм для Вашего случая.
Похоже без аппроксимации дуги в дофига отрезков фиг сделаешь... :(