Всем привет!
Вчера состоялся финал ABBYY Cup 3.0! Хочется сказать большое спасибо всем-всем: кто решал контест, кто помогал его готовить, авторам задач и еще много кому! О том, как прошел День открытых дверей ABBYY, мы расскажем позже, а пока разборы:
Задача A
Утверждение: если прогулка начинается с дерева i и заканчивается в дереве j, то нужно выпилить все деревья до i, все деревья после j и все деревья с отрицательной эстетической привлекательностью между i и j. Для решения подзадачи A1 достаточно для каждой пары деревьев с одинаковой эстетической привлекательностью воспользоваться утверждением и выбрать максимум; ограничения позволяли сделать это хоть за O(n2), хоть за O(n3). Для решения подзадачи A2 требуется такое утверждение: сколько бы ни было деревьев с одинаковой эстетической привлекательностью, нам всегда выгодно рассматривать только пару из самого левого и самого правого таких деревьев. Тогда количество различных рассматриваемых пар сократится до O(n) (с O(n2)), дальше можно делать что угодно, например, считать частичные суммы или брать сумму на отрезке.
Задача B
Для решения подзадачи B1 требовалось проэмулировать поведение Брабобрея в точности так, как описано в условии. Для решения подзадачи B2 достаточно для каждого завершающего бобра хранить взведённый флаг-единичку. Назовём завершающим бобром такого бобра i, что справа от него нет бобра i + 1 (то есть в случае запроса, включающего бобров i и i + 1 придётся запускать Брабобрей ещё один раз). Тогда при обмене пары бобров i и j местами будет всего четыре кандидата, где состояние флага может измениться: i - 1, i, j - 1, j. Ответ на запрос — это просто количество завершающих бобров на отрезке, что уже является классической задачей.
Задача C
Для решения подзадачи C1 можно либо посчитать динамику, либо жадно вычитать наибольшую цифру — несложно доказывается, что всегда требуется вычитать именно наибольшую цифру. Для подзадачи C2 достаточно посчитать динамику для первого миллиона, разбить мысленно число на две группы цифр — старшие разряды и младшие — и выполнять не одно вычитание, а целую серию вычитаний, чтобы мгновенно минимизировать младшие разряды. Для решения подзадачи C3 необходимо уйти от желания хранить в параметрах динамики само число, а хранить лишь количество разрядов.
Задача D
Совершенно очевидно, что судьба бобрактора такова: либо мы пройдём по стрелкам и выберемся, либо уткнёмся в цикл. Во втором случае необходимо найти длину цикла l, но тогда нам нужен лишь остаток от деления времени на длину цикла. Таким образом, мы мысленно избавились от второго случая. Для решения подзадачи D1 достаточно проэмулировать поведение бобрактора, сохраняя на каждом шаге время последнего посещения текущей точки (чтобы определить длину цикла, когда мы на него наступим второй раз). Для решения подзадач D2 и D3 требовалось построить граф перемещений бобрактора, а затем обработать каждый из тестов мультитеста, причём в D2 граф можно построить в лоб, да и найти ответ на каждый тест — пройти по графу в лоб. В D3 предлагается использовать логарифмические структуры данных. В целом, идея решения лежит на поверхности; задача представляет интерес именно с технической точки зрения.
Задача E
Для решения подзадачи E1 необходимо прийти к следующему утверждению: если на ребре x → y есть пометки x и y, идущие подряд, то такое ребро может генерировать искомый путь. Назовём такое ребро инициирующим. Несложно понять, что, зафиксировав инициирующее ребро, дальнейший путь в обе стороны восстанавливается однозначно. Теперь надо понять, что достаточно рассматривать только инициирующие рёбра. Рассмотрим любой требуемый путь в графе. Он содержит p вершин и p - 1 рёбер. Но тогда по принципу Дирихле хотя бы одно ребро должно содержать как минимум две пометки. Пусть какое-то ребро x → y содержит пометки a b, (a, b) ≠ (x, y). Но тогда разрежем этот путь на два по ребру x → y и заметим, что тогда какой-то из двух подпутей уж точно содержит больше пометок, чем есть рёбер. Рассуждая подобным образом можно прийти к выводу, что найдётся хотя бы одно ребро x → y с пометками x и y. Если ни одного инициирующего ребра нет, то искомого пути не существует. Путь, сгенерированный инициирующим ребром — это кратчайший валидный путь для данного инициирующего ребра. К нему можно дописывать входящие и исходящие хвосты так, чтобы путь становился длиннее. Хвосты не должны содержать инициирующих рёбер, потому что инициирующие рёбра генерируют свои пути. Любой валидный путь — это путь из троек ("входящий хвост", "путь инициирующего ребра", "исходящий хвост"), соединённых между собой рёбрами без пометок. Для решения подзадачи E2 можно предподсчитать все хвосты и все сгенерированные инициирующими рёбрами пути, а затем динамикой посчитать количество путей фиксированной длины.











Over 100 lines of code became a single sentence :)
I don't understand the explanation for C[23] at all. Is it just me or is this explanation a bit too short? I'd also have a hard time understanding B just using this explanation, if I hadn't solved it by myself.
Yeah, it is. This editorial ignores the large gaps in ideas for different subtasks — it focuses on the first subtask and only briefly mentions the other ones.
For example, the "logarithmic data structures": what are we supposed to store in those? It says almost nothing at all.
At least, my solution for D is:
in D2, we form a directed graph, whose nodes are states of Beaveractor's movement (x,y coordinates and direction) and one other node corresponds to "outside the campus"; each node has outdegree of 1. This means the graph splits to components, where each component contains at most 1 cycle. We determine those components, for each cycle its length and for every node its distance from the cycle and the node which we get to from this one after passing through b edges — using a BFS. Now, for each query where we go around a cycle, we can in O(1) time jump to the first node on a cycle that we get to, then apply "modulo cycle length" on t (which skips all the traversals of the cycle except the last one), which gives us t <= b^2. Now, while t > b, we jump by b edges, and then by 1 edge, which gives time O(b) per query with O(b^2) pre-computation. This is enough if we have a 6s time limit.
in D3, we can't store the entire graph, so we only remember ends of arrows as nodes. That's enough, because from any point, Beaveractor goes straight ahead until it comes out of the campus or hits an arrow, in which case it'll go straight ahead again until it hits a node (end of an arrow). Using the fact that there's at most 1 turn between any 2 nodes (and we can find where it happens using the mentioned logarithmic structures — an interval tree for vertical arrows — an arrow is an interval of y-coordinates and we remember there, which x-coordinate it has — in which I traverse the path from root to the x-coordinate of the given node and try to find a lower bound on x-coordinates of the intervals I see there and similarly for horizontal intervals), we can easily determine the position between any 2 nodes; the edges are weighted and for every node, we remember the distance and the node we get to after passing 1,2,4,8...2^20 edges (as there some less than 10^6 nodes in the graph), so we can make the skips not in O(sqrt(graph size)), but in O(log(graph size)) time.
Thanks for the nice explanation :) Can somebody explain the idea for C3 as well?
Let me try. First of all, in C2 we can do what's written in the editorial: split the number in two parts(6 digits each), now while the first part is fixed, all we need to know about it is the biggest digit. So we calculate two arrays: cnt[dig][n] — how many operations we need to get to negative number if we can subtract maximum of dig and biggest digit of n, and decr[dig][n] — what is the first negative number we reach this way(here 0 ≤ dig < 10, 0 ≤ n < 106). After that, we can decrease first part by one in O(1) time and that's it.
C3's solution is almost the same, we calculate arrays cnt and decr again using memoization, but we split the number into the first digit and remainder.
Thanks, this was helpful :)
^ Will you please explain "decrease first part by one". I did not get that.
http://codeforces.me/contest/331/submission/4317755 thanks for mmaxio's useful comment . this is a nice problem ... since we are using gready to subtract ... we can use dp. dp state :
dp[i][j]represents that the maximum digit of the previous digits is i, the number is j , the meaning of the state is the minimum number of time needed to make j become a non positive integer. Suppose we've got a number "NOW",eg (NOW=285678, j=85678) we also need to know what is the negative number "decr" that j will become and then subtract the absolute value|decr|from200000. every time , now's highest digit will decrease by 1 ,and this is our state transitionHow do you prove that the greedy algorithm is correct?
I'm just curious and bad at proving. :(
Let f(n) be the minimum number of moves needed to reduce the number n to zero by repeated subtraction of one of its digits.
Let D(n) be the set of digits of a number n. We have the recurrence f(0) = 0,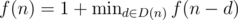 .
.
I will prove to you by induction that f(n) is monotonically increasing, which means that subtracting more is always better, which implies that the greedy approach is correct.
Claim: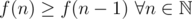
Base case: Obviously f(1) = 1 ≥ 0 = f(0), so the claim holds for n = 1
Inductive step: Let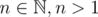 and
and 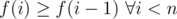 (so f is monotone on the set {0, ..., n - 1}). Let k be the largest digit of n. By a simple case analysis, we can see that n - 1 has a digit l ≥ k - 1. Using the monotonicity of f, we conclude
(so f is monotone on the set {0, ..., n - 1}). Let k be the largest digit of n. By a simple case analysis, we can see that n - 1 has a digit l ≥ k - 1. Using the monotonicity of f, we conclude
In addition, we know that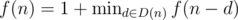 . Since k = max D(n) and because we assumed the monotonicity of f on the set {0, ..., n - 1}, we know that f(n) = 1 + f(n - k). Combined with the above inequality, this gives us f(n) ≥ f(n - 1).
. Since k = max D(n) and because we assumed the monotonicity of f on the set {0, ..., n - 1}, we know that f(n) = 1 + f(n - k). Combined with the above inequality, this gives us f(n) ≥ f(n - 1).
Честно говоря — ничего не понял!
I hate this editorial, just like Meg.