Задача G. "Очередь"
Данная задача имеет несколько возможных решений, но я расскажу 2 возможных подхода:1. Декартово дерево (дуча, treap или дерамида)
Будем считать, что читатели знакомы с этой структурой (если это не так, то советую почитать тут). Самое простой по логике подход использует неявное декартово дерево, и этот алгоритм действует так: будем добавлять людей по очереди, в порядке их прихода. В вершине дерева, кроме служебной информации, будем поддерживать число maxValue, равное максимальному значению из чисел ai в этом дереве.Бинарным поиском переберем возможную позицию нового человека, пусть он имеет номер k, pos от 0 до ck (для удобства нумерацию введем с конца очереди). Человек достигнет этой позиции тогда и только тогда, когда среди чисел ai, 0 ≤ i < pos не существует ни одного, большего числа ak. Это можно проверить, отщепив от декартова дерева поддерево размера pos, и проверив у него число maxValue. Таким образом мы найдем значение pos, и в эту позицию вставим нового человека. Построив полную очередь, нужно вывести ответ. Но это очень простая операция, не будем ее обсуждать. Асимптотика такого решения
 . Замечу, что это решения является неоптимальным, и вполне возможно, что оно не всегда пройдет по времени, поэтому модифицируем его:
. Замечу, что это решения является неоптимальным, и вполне возможно, что оно не всегда пройдет по времени, поэтому модифицируем его:избавимся от бинарного поиска. Для этого можно сразу отщепить от дерева поддерево размера ck с начала дерева, и найти в нем такую максимальную позицию pos, что все числа ai (0 ≤ i < pos) меньше ak. Это делается с помощью одного обхода вниз по дереву, где на каждой вершине мы смотрим, надо ли закончить спуск, или надо выбрать одного из сыновей и продолжить. В процессе такого пути накапливаем количество вершин, оставляемых слева от текущей. Потом вставляем нового человека в найденную позицию, и восстанавливаем дерево обратно. Подумайте сами, как это реализовать, это не очень сложно. Асимптотика нового решения уже составляет
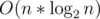 .
. 2. Использование метода  -декомпозиции.
-декомпозиции.
Пусть 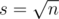 . Тогда мы заведем s двусвязных списков, которые и будут представлять очередь, только разбитую на части. Так же, как и в предыдущем решении, будем добавлять по одному человеку в очередь в порядке их прихода.
. Тогда мы заведем s двусвязных списков, которые и будут представлять очередь, только разбитую на части. Так же, как и в предыдущем решении, будем добавлять по одному человеку в очередь в порядке их прихода.Будем хранить для каждого списка также число maxValue, равное максимальному значению из чисел ai в этом списке. Тогда добавление происходит так: будем искать подходящее место для нового человека, для этого пропустим все списки, суммарной длиной, меньшей ck, причем во всех этих списках числа maxValue должны быть меньше, чем ak. Если мы возьмем первый такой список, где это условие не выполняется, или ck стало меньше, чем длина пропущенных список плюс длина текущего, то мы по такому списку пробежимся "в лоб", то есть по каждому элементу от начала до конца, проверим выполнение условий, и добавим нового человека на найденное место.
Давайте оценим, сколько времени требует текущее решение. В худшем случае, оно будем всех людей добавлять в один и тот же список, и при добавлении нового "в лоб" пробегаться от его начала до конца, таким образом в неудачном случае, время работы составит O(n2), что нам не очень годится.
Тогда применим следующую хитрость: в момент, когда какой-либо список станет больше, чем 2 * s элементов, то сделаем перераспределение людей в очереди. Из списков, которые содержат более s элементов, будем проталкивать их в следующую очередь. Таким образом мы нормируем списки, и они станут достаточно короткие - всего не более s элементов в каждом.
Оценим время работы в новом случае. Теперь добавление нового человека требует
 времени. Нормализация требует O(n) времени, но выполняется она не чаще, чем раз в
времени. Нормализация требует O(n) времени, но выполняется она не чаще, чем раз в  операций добавления, что в сумме даст
операций добавления, что в сумме даст 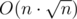 операций.
операций.Значит, наше решение работает за
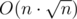 .
.










Судя по табличке сданных решений, корневая оптимизация здесь ещё и короче пишется, чем большинство деревьев.
Лучше использовать deque.
Но vector<vector<int> > - все равно плохая конструкция. Лучше использовать vector<int>[] если возможно.