Disclaimer: This problem is from a contest on Hackerearth(hiring for intern) held on 13th April.
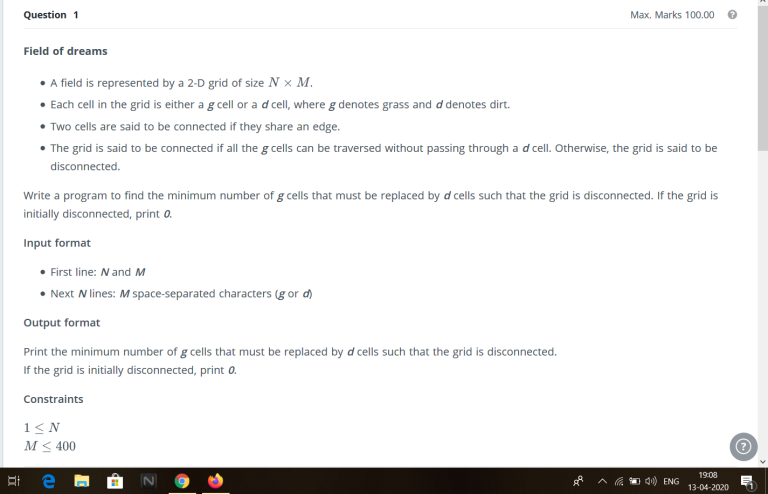
I was unable to solve this problem, can anyone help how to solve it? Can it be solved greedily or we need to use some graph algo?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
Disclaimer: This problem is from a contest on Hackerearth(hiring for intern) held on 13th April.


I was unable to solve this problem, can anyone help how to solve it? Can it be solved greedily or we need to use some graph algo?
| Name |
|---|



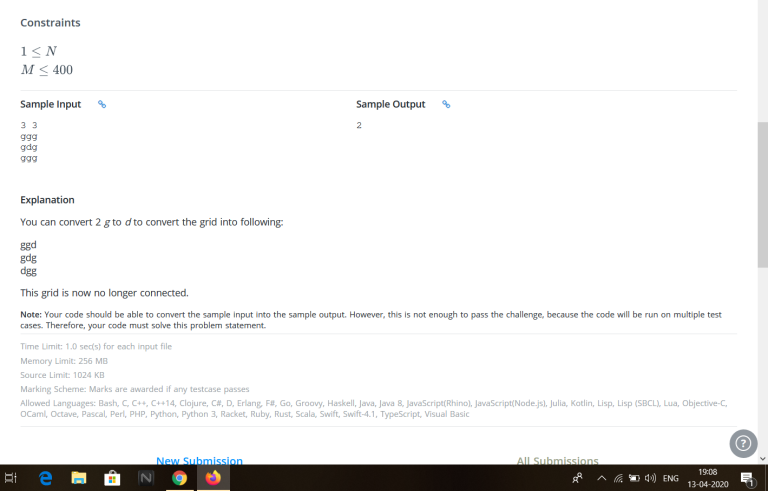
The answer doesn't exceed 2. When the answer is 0, grid is already disconnected. When the answer is 1... , I don't have so good solution, but I'm glad if you read this.
First, if there is a cycle made of G, grid can't be disconnected by this part. Find them by searching Ds which don't touch edges of the grid, then replace all D in the cycle.
Second, find G which have several relatives like followings.
The grid has no cycles, so replacing this G will disconnect the grid.
One more solution which i guess is correct:
1) if grid is already disconnected, answer is 0.
2) if it has an articulation point then answer 1.
3) else answer is 2 (because we can always isolate some corner g by placing 2 d's).
Special case: if there is exactly 1 g then answer is obviously 1.
if there is exactly 1 g, or exactly 2 connected g, then answer is obviously NO SOLUTION
Why no solution, we can replace those g's by d and the grid is disconnected.
also the problem doesn't mention anything like NO SOLUTION.
https://en.wikipedia.org/wiki/Vacuous_truth
What do you expect from HackerEarth?
Oh wow! I didn't knew this before. Thanks for the link.
But that means either the author assumes that if there are all d's then it is disconnected or the problem statement lacks this information.
Because the condition "all the g cells can be traversed ... " literally holds.