Сегодня на контест мы дали задачку про обратный рюкзак.
Мы, кроме того, умеем почти так же решать обычный рюкзак с бесконечными предметами, если решить его для отрезка [1..m], то есть получить многочлен с коэффициентами 1 там, где можно получить такую сумму и 0 — там где нельзя. К этому многочлену нужно на отрезкок [m+1..2m] добавить единицы в те позиции, где есть предметы. Потом полученный многочлен возвести в квадрат. Тогда мы решили задачу за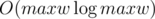 
. Мне интересно, это боян?
UPD: это все бред, недостаточно просто возводить в квадрат =(
UPD: но достаточно два раз возвести в квадрат!
Я не очень хорошо понял.
1) коэффициенты, которые мы хотим получить, видимо не 1, а больше 0.
2) можно подробней пояснить про то, как строится полином, и если мы только на отрезок [m+1..2m] добавляем единицы, у нас ведь не появится ненулевых коэффициентов на отрезке [1..m]?
Решение за
Возьмем многочлен, где единицы стоят на местах, соответствующих весу предметов. Возведем его в m-тую степень (или в любую большую). (будем возводить в квадрат и отбрасывать лишнее).
1) да, мы все, что больше нуля приведем к 1 (но чисел меньших 1 не будет, по идее) 2) ну да, я немного не прав в посте. рассмотрим суммы на отрезке [m+1..2m] она может быть скомбинирована из нескольких сумм на [0..m] или одного предмета из отрезка [m+1..2m] и ровно одной суммы из отрезка [0..m]. Поэтому, если мы возведем в m-тую степень многочлен для [0..m] (возведем в квадрат, отбросим лишнее итд), а потом допишем единицы в коэффициенты, соответствующие весам предметов и возведем еще раз в квадрат, то все будет хорошо. Но это, увы, тоже
. Я почему-то решил, что можно возводить только в квадрат. Надо подумать, может я что-то забыл.
ОК.
Еще я не понимаю, зачем нам нужно [m+1..2m], нам ведь нужно только для элементов <= m знать, могут ли они быть представимы в виде суммы элементов из входа.
не, ну у меня двойное тут обозначение получилось. мы начинаем с m = 1 и удваиваем его, пока оно не станет больше maxw
Аааа... Ну это видимо тогда O(MlogM).
я вдруг понял, что если у нас в некоторый момент есть предмет 2*m/3 и мы допишем единичек, а потом возведем в квадрат, то у нас получится, что сумма 2*m может быть недоступна. То есть, чтобы удваивать, нужно изначально половинку возводить в какую-то степень. Вроде бы, в константную, но не в первую. Этот момент надо аккуратнее продумать.
Можно понять, что на каждом шаге достаточно просто два раза возводить в квадрат.
Потому что, если число представимо в виде более чем 4 чисел, то два минимальных должны в сумме давать > m, иначе можно уменьшить количество чисел в представлении. А это значит, что второе по минимальности > (m / 2), что значит что сумма > (2 * m).
О, да, действительно, спасибо
Это тоже самое что и Rotate the optimization problem здесь ?
Я, честно говоря, не совсем понял, что там имеется в виду, но, вроде, не это.