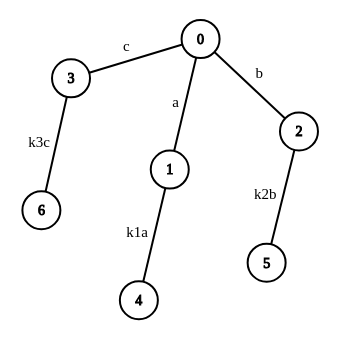
Is there a well known trick in max-flow, in which after entering a node or edge the flow through it multiplies by some constant k, which can be different for each node. Something like described in the image above.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |

Is there a well known trick in max-flow, in which after entering a node or edge the flow through it multiplies by some constant k, which can be different for each node. Something like described in the image above.
| Name |
|---|



If you are just doing multiplications at each node rather than additions, you can just take the log of each weight and the problem is reduced to a normal max-flow. For example ln(a*k1) = ln(a)+ln(k1). So just solve the graph using logs, then your final answer e to the answer that you get from that process. (Though this of course introduces lots of rounding error and may not be acceptable for the application)
But by this method, i think every time you have two or more incoming edges, their net flow will multiply instead of adding, eg log(a) + log(b) = log(ab).
Ah, I was imagining finding 1 path at a time and then removing the used edges but I guess that general algorithms use augmenting paths, so having 2 incoming edges will be a problem. I'm not sure what you're talking about adding constant flow, unless you're talking about a different problem than max-flow... maybe I just don't understand the problem well enough without formal statement.
For example in the above picture, whenever an incoming flow(say a) flows through an vertex, than outgoing flow is increased by by constant k and becomes(a+k)(only when a is non-zero). As you said the problem doesn't actually comes under max-flow statement since incoming flow != outgoing flow for a non source-sink vertex, but i was wondering if it could be converted into one, through some other modeling.
Ok, I see what you mean more now. I don't think my method will work at all if addition is involved. I still am unclear about a few things of the statement though. Are we trying to maximize flow out of the source or into the sink? And when does constant flow get added? Is it just when you enter a node? Also, you say flow can be multiplied after entering a node or edge. One observation is that this is equivalent to just being multiplied after entering an edge (since we can just multiply the 'leaving a node' cost by the 'entering a node' cost).
Besides, can you share how you add an extra constant flow, whenever you enter a node(say A), ofcourse we can add an extra edge from source to node but that would increase the flow by the constant k, even when netflow through A was 0 previously, but that is undesired in my case.
I believe not. Find another modeling.
Thanks, i too was thinking of the same.