Butskhrikidze's blog

Stern–Brocot tree
By Butskhrikidze, history, 6 years ago, In English

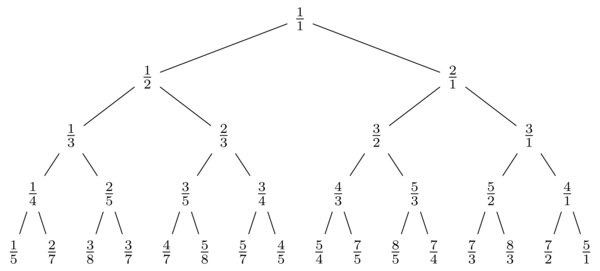
see tutorial about stern-brocot's tree Tutorial. this is infinity binary tree which nodes are irreducible fractions. enumerate nodes of tree using BFS. it is given one number n and one fraction . Your task is to determine what fraction is written on the node LCA(n, ) where LCA is Lowest Common Ancestor of nodes n and . (in first case node is defined by its number and in second case node is defined by fraction). 0 < a, b < 109 and 0 < n < 1018.

what is efficient method for finding what fraction is written on the node by its fraction and vice versa?

see example of tree

  • Vote: I like it
  • +2
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it -10 Vote: I do not like it

Auto comment: topic has been updated by Butskhrikidze (previous revision, new revision, compare).

→ Reply
»
6 years ago, # |
  Vote: I like it -18 Vote: I do not like it

can anyone help me?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For finding what fraction corresponds to some numbered node you can look at GCD for some ideas. If we have some a,b, we can get the parent by determining the smaller of the two and subtracting it from the larger. With a,b <= 10^9 we could have 1, 10^9 and therefore take 10^9 steps to get to the base of the tree, so we should instead group those. Say we have some b >= xa. That means that we must have taken x steps in the same direction in the tree, so we can push x moves right or left into our path.

For the reverse it's much simpler. if we consider this tree as a BIT then each bit 1 or 0 in N except its most significant bit corresponds exactly to one move to our left or right child. Since there's at most 64 bits in N we can quickly and easily generate our a/b pair by following those steps.

→ Reply