Hey! I have a question. If I have to calculate a pow b modulo mod, with b>mod, is it the same with a pow (b % (mod-1)?
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
10:39:41
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
10:39:41
Зарегистрироваться »
*есть доп. регистрация
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 06:55:20 (l3).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











By Euler's Theorem, if gcd(a, n) = 1,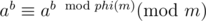 . If m happens to be a prime, then phi(m) = m - 1.
. If m happens to be a prime, then phi(m) = m - 1.
If "gcd(a,n)=1", you mean gcd(a,m)=1? I can not see the n
Upps, sorry. You're right, that was meant to be an m :)
Thanks!
Even when gcd(a, n) > 1, the following holds: If b ≥ φ(m),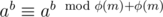 . When m is large and you cannot efficiently factor it to compute φ(m) and b is given in decimal form, you can still use fast exponentiation. Process digits of b one by one starting from the most significant one and use a10b + c = (ab)10 × ac.
. When m is large and you cannot efficiently factor it to compute φ(m) and b is given in decimal form, you can still use fast exponentiation. Process digits of b one by one starting from the most significant one and use a10b + c = (ab)10 × ac.