После раунда я увидел несколько интересных ссылок в комментариях.
Задача С: https://www.quora.com/What-is-the-radius-of-the-circle-surrounding-a-circle-if-all-the-surrounding-circles-are-equal — ну тут без комментариев :/
Задача F: Из условия поймем, что нам нужно найти "подмножество с максимальным XOR`ом" на отрезке с L по R. Эту подзадачу очень легко загуглить (https://www.geeksforgeeks.org/find-maximum-subset-xor-given-set/)
Такая же задача: https://blog.csdn.net/ShadyPi/article/details/79939990
Можно увидеть много успешных посылок с этой же идеей :|
Problem E: https://www.geeksforgeeks.org/assign-directions-to-edges-so-that-the-directed-graph-remains-acyclic/ — такая же идея с тем, что-бы ориентировать ребра в порядке топологической сортировки.
Спасибо Rinne and M_H_H_7 за ссылки в комментариях (https://codeforces.me/blog/entry/64495?#comment-484476, https://codeforces.me/blog/entry/64495?#comment-484418).
A bit notorious.
It would be useful to enclose the spoilers in spoiler tags.
We have discussed the problem D with similar constraints (actually, they doesn't matter) in our math training session. Also, the solution was exactly the same as the tutorial.
I found the link while writing this comment, check 091 here: http://olympiads.win.tue.nl/imo/soviet/RusMath.html
Maybe it is only my problem, but why are you trying so hard to google the problems? Both C and E are faster to solve by yourself than find the solution on the internet.
About F: article from geeksforgeeks doesn't tell you how to solve the problem (maybe its because geeksforgeeks is trash? idk). There are some words about Gaussian elimination but I don't think that you can understand that unless you already know that XOR is sum of vectors in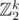
. And about the same problem — it is in Chinese! Do you think that problemsetters must learn Chinese? Even the guy who wrote the original comment about that problem existence mentioned that it is 100% coincidence.
About D from comments: the problems are not the same. This is how problemsetting works: you take something already existing and change it to get new problem.
Problems are same, actually. The ASU problem is solved by finding the algorithm.
Rooks are moving by chess rules instead of jumping to any point. This one is enough for problems to be different. Algorithms maybe the same, but the proofs that it works are different.
I didn't google this problems. Links were in the comments.
The fact remains. Person who is not able to solve this problems can simply google them.