IOI 2018 tasks webpage (multiple languages).
→ Pay attention
Before contest
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
4 days
Register now »
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
4 days
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/26/2024 19:54:38 (j2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Isn't it possible to solve the first task with only N — 1 switches?
By making a heap-like tree of switches and connecting output of leaf switches to the corresponding triggers, and connecting output of triggers to the root of the tree.
Switches need to be returned to X by the end.
Since all the switches have to return back to state X we will need a perfect binary tree. This will result in 2n switches. With this approach I got 53 points in contest
What's the solution for Meeting Points
The task is quite hard. You need some nice ideas and it took me quite long to implement. My solution can probably be simplified.
For a fixed range [l, r] consider the Cartesian tree of H[l..r] and do some dp on it.
Computing the Cartesian tree each time is slow, but we can deduce all dp-values except the last one if we precompute the dp for Cartesian trees of all prefixes and suffixes.
Doing that is still quadratic, but we can speed it up by doing scanline and querying offline. The dp transitions are a bunch of linear functions where dependencies change at most O(n) time. This reduces the runtime to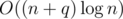 .
.
Break ties between equal elements by their position.
Lets first consider a single query range [l, r]. The the solution can be computed by a DP on the max-Cartesian tree of H[l..r]: For a node n let DP[n] be the answer for its subtree. The computations then is as follows
as n is the root of its subtree, hence maximal, so it does not make sense to meet at n, so we meet in one of the subtrees and the nodes from the other subtree need to cross n.
Building the Cartesian tree for each query range is to slow. To speed it up, note that for a fixed n, the subtree of n.r in the Cartesian tree of H[1..r] is the same as the subtree of n.r in the Cartesian tree of H[l..r]. Symmetric things hold for n.l in H[l..end]. Hence we only need to precompute prefixes and suffixes and do one transition step to compute DP[n]. (n can be found by range maximum query.)
The Cartesian trees of prefixes can be built incrementally by adding elements from left to right. (Wikipedia)
After adding a new element, we need to recompute the dp on the right (left for suffixes) spine of the tree. There might be Θ(n) nodes on it, so we can't do it naively.
Lets look at the dp transition again and focus on the case where n is in the right spine.
We can write this as
where a and b wont change during the scanline. Lets call nodes where a + n.r.size·n.H is smaller L-nodes and nodes where DP[n.r] + b is strictly smaller R-nodes. On the right spine, lets call a maximum contiguous subset of R-node followed by an L-node a block.
One observation is that when adding more nodes, an L-node might change to an R-node but not the other way around. (If a node was added and n is still on the spine, the its H was smaller than n.H, so the increase in DP[n.r] is smaller than the increase of n.H in n.r.size·n.H.) Newly added nodes are always L-nodes.
For a block with L-node n, the dp values are linear with slope n.H. For every block, we thus just have to maintain every nodes value and constant term in the dp (in a
std::deque)and a global slope and a global constant offset. For the L-node we store the whole node. The blocks are then stored in astd::set, sorted by their order on the spine.The time where a L-node becomes a R-node can be computed as the intersection between two lines. I maintain all these times as events in a priority queue. As every such event reduces the number of block, there are at most n such events. When an event happens, two blocks get merged. We can merge the smaller block into the larger one by adjusting the global offset and merging the deques. This takes amortized time.
time.
When looking for a node to answer a query, just binary search in the set to find the block, then binary search in the block to find the node.
Overall, the scanline loop looks like this:
My solution passes in 3.5s on the Yandex mirror (limit is 4.5s). The total runtime is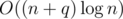 with O(n + q) memory.
with O(n + q) memory.
Mirror for Day 2 is up!
Editorials and tests for both contest days are up at https://ioi2018.jp/competition/tasks/!