#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin >> n;
int a, b, c, d;
cin >> a >> b >> c >> d;
int S = a + b + c + d;
int Ans = 1;
for(int i = 2; i <= n; i++)
{
cin >> a >> b >> c >> d;
if(a + b + c + d > S)
{
Ans++;
}
}
printf("%d\n",Ans);
return 0;
}
#include <bits/stdc++.h>
using namespace std;
long long ar[4];
char c1[4] = {'0', '0', '1', '1'};
char c2[4] = {'0', '1', '0', '1'};
int main() {
int n;
cin >> n;
string a, b;
cin >> a >> b;
for(int i = 0; i < n; i++){
for(int j = 0; j < 4; j++){
if(c1[j] == a[i] && c2[j] == b[i]){
ar[j]++;
}
}
}
cout << ar[0] * ar[2] + ar[0] * ar[3] + ar[1] * ar[2] << endl;
return 0;
}
#include <bits/stdc++.h>
using namespace std;
#define MAXN 100000
#define rint register int
inline int rf(){int r;int s=0,c;for(;!isdigit(c=getchar());s=c);for(r=c^48;isdigit(c=getchar());(r*=10)+=c^48);return s^45?r:-r;}
int n, L, A[MAXN+5];
int main()
{
n = rf();
L = (int)sqrt(n);
for(rint i = 1, o = n, j; i <= n; i += L)
for(j = min(i+L-1,n); j >= i; A[j--] = o--);
for(rint i = 1; i <= n; i++)
printf("%d%c",A[i],"\n "[i<n]);
return 0;
}
#include <bits/stdc++.h>
using namespace std;
#define MAXN 100000
#define rint register int
inline int rf(){int r;int s=0,c;for(;!isdigit(c=getchar());s=c);for(r=c^48;isdigit(c=getchar());(r*=10)+=c^48);return s^45?r:-r;}
int Wu[4096], f[64][64][104], g[4096][104], w[16], m, n, q, E, K, B = 6, L = 63, H = 4032; char _[16];
int main()
{
m = rf();
n = rf();
q = rf();
generate(w,w+m,rf);
E = 1<<m;
for(rint S = 0, j; S < E; S++)
{
for(j = 0; j < m; j++)
S&1<<j?:Wu[S]+=w[j];
Wu[S] = min(Wu[S],101);
}
for(rint i = 1, j, S; i <= n; i++)
{
scanf("%s",_+1);
for(S = 0, j = m; j; j--)
S = S<<1|(_[j]^'0');
for(j = 0; j < 64; j++)
++f[(S&H)>>B][j][Wu[((j^(S&L))|H)&~-E]];
}
for(rint S = 0, a, b, j; S < E; S++)
{
for(j = 0; j < 64; j++)
for(a = 0, b = Wu[(((j<<B)^(S&H))|L)&~-E]; b <= 100; a++, b++)
g[S][b] += f[j][S&L][a];
partial_sum(g[S],g[S]+101,g[S]);
}
for(rint i = 1, j, S; i <= q; i++)
{
scanf("%s",_+1);
for(S = 0, j = m; j; j--)
S = S<<1|(_[j]^'0');
printf("%d\n",g[S][rf()]);
}
return 0;
}
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define rint register int
inline int rf(){int r;int s=0,c;for(;!isdigit(c=getchar());s=c);for(r=c^48;isdigit(c=getchar());(r*=10)+=c^48);return s^45?r:-r;}
//=====Computational Geometry Definitions
struct Vec
{
int x,y; Vec(){} Vec(int _x, int _y){x=_x,y=_y;} inline Vec operator + (Vec b){return Vec(x+b.x,y+b.y);}
inline Vec operator - (Vec b){return Vec(x-b.x,y-b.y);} inline Vec operator - (){return Vec(-x,-y);}
inline ll operator * (Vec b){return (ll)x*b.x+(ll)y*b.y;} inline ll operator % (Vec b){return (ll)x*b.y-(ll)b.x*y;}
inline ll operator ~ (){return (ll)x*x+(ll)y*y;} inline bool operator < (const Vec &b)const{return x^b.x?x<b.x:y<b.y;}
inline bool operator ==(Vec b){return x==b.x&&y==b.y;} inline bool operator !=(Vec b){return x^b.x||y^b.y;}
}; typedef Vec Pt; inline bool ToLeft(Vec a, Vec b){return b%a>0;} inline bool Para(Vec a, Vec b){return !(a%b);}
Pt LTL; inline bool cmpltl(Pt a, Pt b){a = a-LTL; b = b-LTL; return Para(a,b) ? ~a<~b : ToLeft(b,a);}
typedef vector<Pt> Poly; Poly A, B, C, D; typedef vector<ll> Str; Str T, S; int n, m; vector<int> nex;
//=====
void CH(Poly &A, Poly &R)
{
R.push_back(Pt());
LTL = *min_element(A.begin(),A.end());
sort(A.begin(),A.end(),cmpltl);
for(rint i = 0; i < (int)A.size(); i++)
{
for(; R.size()>2&&!ToLeft(A[i]-R.back(),R.back()-R[R.size()-2]); )
R.pop_back();
R.push_back(A[i]);
}
R[0] = R[R.size()-1];
R.push_back(R[1]);
}
void CTOS(Poly &p, Str &s)
{
s.push_back(0);
for(rint i = 1; i < (int)p.size()-1; i++)
{
s.push_back(~(p[i]-p[i-1]));
s.push_back((p[i]-p[i-1])%(p[i+1]-p[i]));
}
}
void CalNex()
{
nex.resize(m+1);
for(rint i = 2, j = 1; i <= m; i++)
{
for(; j>1&&S[i]^S[j]; )
j = nex[j-1]+1;
j += S[i]==S[j];
nex[i] = j-1;
}
}
bool KMP()
{
for(rint i = 1, j = 1; i <= n; i++)
{
for(; j>1&&(j>m||T[i]^S[j]); )
j = nex[j-1]+1;
j+=T[i]==S[j];
if(j>m)
return true;
}
return false;
}
int main()
{
A.resize(rf()); B.resize(rf());
for(rint i = 0, s = (int)A.size(); i < s; i++)
A[i].x = rf(), A[i].y = rf();
CH(A,C);
CTOS(C,T);
n = T.size()-1;
for(rint i = 0, s = (int)B.size(); i < s; i++)
B[i].x = rf(), B[i].y = rf();
CH(B,D);
CTOS(D,S);
m = S.size()-1;
for(rint i = 1, s = (int)T.size(); i < s; i++)
T.push_back(T[i]);
n <<= 1;
CalNex();
puts(KMP()?"YES":"NO");
return 0;
}
#pragma comment(linker, "/STACK:512000000")
#define _CRT_SECURE_NO_WARNINGS
//#include "testlib.h"
#include <bits/stdc++.h>
using namespace std;
#define all(a) a.begin(), a.end()
using li = long long;
using ld = long double;
void solve(bool);
void precalc();
clock_t start;
int main() {
#ifdef AIM
freopen("/home/alexandero/CLionProjects/ACM/input.txt", "r", stdin);
//freopen("/home/alexandero/CLionProjects/ACM/output.txt", "w", stdout);
//freopen("out.txt", "w", stdout);
#else
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
#endif
start = clock();
int t = 1;
#ifndef AIM
cout.sync_with_stdio(0);
cin.tie(0);
#endif
cout.precision(20);
cout << fixed;
//cin >> t;
precalc();
while (t--) {
solve(true);
}
cout.flush();
#ifdef AIM1
while (true) {
solve(false);
}
#endif
#ifdef AIM
cerr << "\n\n time: " << (clock() - start) / 1.0 / CLOCKS_PER_SEC << "\n\n";
#endif
return 0;
}
//BE CAREFUL: IS INT REALLY INT?
template<typename T>
T binpow(T q, T w, T mod) {
if (!w)
return 1 % mod;
if (w & 1)
return q * 1LL * binpow(q, w - 1, mod) % mod;
return binpow(q * 1LL * q % mod, w / 2, mod);
}
template<typename T>
T gcd(T q, T w) {
while (w) {
q %= w;
swap(q, w);
}
return q;
}
template<typename T>
T lcm(T q, T w) {
return q / gcd(q, w) * w;
}
template <typename T>
void make_unique(vector<T>& vec) {
sort(all(vec));
vec.erase(unique(all(vec)), vec.end());
}
template<typename T>
void relax_min(T& cur, T val) {
cur = min(cur, val);
}
template<typename T>
void relax_max(T& cur, T val) {
cur = max(cur, val);
}
void precalc() {
}
#define int li
//const li mod = 1000000007;
//using ull = unsigned long long;
struct Point {
int x, y;
Point() {}
Point(int x, int y) : x(x), y(y) {}
Point operator - (const Point& ot) const {
return Point(x - ot.x, y - ot.y);
}
int operator * (const Point& ot) const {
return x * ot.y - y * ot.x;
}
void scan() {
cin >> x >> y;
}
bool operator < (const Point& ot) const {
return make_pair(x, y) < make_pair(ot.x, ot.y);
}
int sqr_len() const {
return x * x + y * y;
}
long double get_len() const {
return sqrtl(sqr_len());
}
int operator % (const Point& ot) const {
return x * ot.x + y * ot.y;
}
};
struct Polygon {
vector<Point> hull;
Polygon(int n) {
vector<Point> points(n);
for (int i = 0; i < n; ++i) {
points[i].scan();
}
sort(all(points));
vector<Point> up, down;
for (auto& pt : points) {
while (up.size() > 1 && (up[up.size() - 2] - up.back()) * (pt - up.back()) >= 0) {
up.pop_back();
}
up.push_back(pt);
while (down.size() > 1 && (down[down.size() - 2] - down.back()) * (pt - down.back()) <= 0) {
down.pop_back();
}
down.push_back(pt);
}
hull = up;
for (int i = (int)down.size() - 2; i > 0; --i) {
hull.push_back(down[i]);
}
}
int sqr_len(int pos) const {
return (hull[(pos + 1) % hull.size()] - hull[pos]).sqr_len();
}
int size() const {
return (int)hull.size();
}
long double get_angle(int pos) const {
auto a = hull[(pos + 1) % hull.size()] - hull[pos], b = hull[(pos + hull.size() - 1) % hull.size()] - hull[pos];
long double co = (a % b) / a.get_len() / b.get_len();
return co;
}
};
void solve(bool read) {
vector<Polygon> polys;
int n[2];
cin >> n[0] >> n[1];
for (int i = 0; i < 2; ++i) {
polys.emplace_back(n[i]);
}
if (polys[0].size() != polys[1].size()) {
cout << "NO\n";
return;
}
vector<long double> all_lens;
int m = polys[0].size();
for (int i = 0; i < m; ++i) {
all_lens.push_back(polys[0].sqr_len(i));
all_lens.push_back(polys[0].get_angle(i));
}
all_lens.push_back(-1);
for (int j = 0; j < 2; ++j) {
for (int i = 0; i < m; ++i) {
all_lens.push_back(polys[1].sqr_len(i));
all_lens.push_back(polys[1].get_angle(i));
}
}
/*for (int x : all_lens) {
cout << x << " ";
}
cout << "\n";*/
vector<int> p(all_lens.size());
for (int i = 1; i < p.size(); ++i) {
int j = p[i - 1];
while (j > 0 && all_lens[i] != all_lens[j]) {
j = p[j - 1];
}
if (all_lens[i] == all_lens[j]) {
++j;
}
p[i] = j;
if (p[i] == 2 * m) {
cout << "YES\n";
return;
}
}
cout << "NO\n";
}
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define uint unsigned int
#define rint register int
inline int rf(){int r;int s=0,c;for(;!isdigit(c=getchar());s=c);for(r=c^48;isdigit(c=getchar());(r*=10)+=c^48);return s^45?r:-r;}
bitset<100000032> _b; int n; uint A, B, C, D, Ans;
inline uint f(int p){
return((A*p+B)*p+C)*p+D;
}
inline int cnt(int p, int n){
int r=0;
for(;n/=p;r+=n);
return r;
}
inline auto b(int i)->decltype(_b[0]){
return _b[(i&1)&&(i%6!=3)?i/6<<1|((i%6)>1):0];
}
inline auto b2(int i)->decltype(_b[0]){
return _b[i/6<<1|1];
}
inline auto b3(int i)->decltype(_b[0]){
return _b[i/6<<1];
}
int main()
{
n = rf();
A = rf();
B = rf();
C = rf();
D = rf();
_b[0] = 1;
Ans = cnt(2,n)*f(2)+cnt(3,n)*f(3);
for(rint i = 5, j, z, c, w; i <= n; i += 4){
if(!b2(i))
{
Ans += cnt(i,n)*f(i);
if(i <= 20000){
w = i + i;
c = w % 6;
z = (i * i) % 6;
if(c == 0){
if(z == 1){
for(j = i * i; j <= n; j += w){
b3(j) = 1;
}
}else if(z == 5){
for(j = i * i; j <= n; j += w){
b2(j) = 1;
}
}
}else if(c == 2){
if(z == 1){
for(j = i * i; j <= n; j += w){
b3(j) = 1;
j += w + w;
if(j <= n){
b2(j) = 1;
}
}
}else if(z == 5){
for(j = i * i; j <= n; j += w + w){
b2(j) = 1;
j += w;
if(j <= n){
b3(j) = 1;
}
}
}
}else if(c == 4){
if(z == 1){
for(j = i * i; j <= n; j += w + w){
b3(j) = 1;
j += w;
if(j <= n){
b2(j) = 1;
}
}
}else if(z == 5){
for(j = i * i; j <= n; j += w){
b2(j) = 1;
j += w + w;
if(j <= n){
b3(j) = 1;
}
}
}
}
}
}
i += 2;
if(i <= n && !b3(i))
{
Ans += cnt(i,n)*f(i);
if(i <= 20000){
w = i + i;
c = w % 6;
z = (i * i) % 6;
if(c == 0){
if(z == 1){
for(j = i * i; j <= n; j += w){
b3(j) = 1;
}
}else if(z == 5){
for(j = i * i; j <= n; j += w){
b2(j) = 1;
}
}
}else if(c == 2){
if(z == 1){
for(j = i * i; j <= n; j += w){
b3(j) = 1;
j += w + w;
if(j <= n){
b2(j) = 1;
}
}
}else if(z == 5){
for(j = i * i; j <= n; j += w + w){
b2(j) = 1;
j += w;
if(j <= n){
b3(j) = 1;
}
}
}
}else if(c == 4){
if(z == 1){
for(j = i * i; j <= n; j += w + w){
b3(j) = 1;
j += w;
if(j <= n){
b2(j) = 1;
}
}
}else if(z == 5){
for(j = i * i; j <= n; j += w){
b2(j) = 1;
j += w + w;
if(j <= n){
b3(j) = 1;
}
}
}
}
}
}
}
printf("%u\n",Ans);
return 0;
}
#include <bits/stdc++.h>
using namespace std;
typedef unsigned int ll;
const ll maxn=4e8;
const ll maxp=sqrt(maxn)+10;
ll f[4][maxp],g[4][maxp];
ll n,m,A,B,C,D,ans,res,tmp,rt;
ll p1(ll x){
ll y=x+1; if (x%2==0) x/=2; else y/=2;
return x*y;
}
ll p2(ll x){
long long y=x+1,z=x*2+1;
if (x%2==0) x/=2; else y/=2;
if (z%3==0) z/=3; else if (x%3==0) x/=3; else y/=3;
return (ll)x*y*z;
}
ll p3(ll x){
ll y=p1(x);
return y*y;
}
bool is_prime(ll x){
for (ll i=2;i*i<=x;i++) if (x%i==0) return false;
return true;
}
ll solve(ll n)
{
ll i,j,rt,o[4];
for (m=1;m*m<=n;m++) {
f[0][m]=(n/m-1);
f[1][m]=(p1(n/m)-1)*C;
f[2][m]=(p2(n/m)-1)*B;
f[3][m]=(p3(n/m)-1)*A;
}
for (i=1;i<=m;i++) {
g[0][i]=(i-1);
g[1][i]=(p1(i)-1)*C;
g[2][i]=(p2(i)-1)*B;
g[3][i]=(p3(i)-1)*A;
}
for (i=2;i<=m;i++) {
if (g[0][i]==g[0][i-1]) continue;
o[0]=1; for (int w=1;w<4;w++) o[w]=o[w-1]*i;
for (j=1;j<=min(m-1,n/i/i);j++)
for (int w=0;w<4;w++)
if (i*j<m) f[w][j]-=o[w]*(f[w][i*j]-g[w][i-1]);
else f[w][j]-=o[w]*(g[w][n/i/j]-g[w][i-1]);
for (j=m;j>=i*i;j--)
for (int w=0;w<4;w++)
g[w][j]-=o[w]*(g[w][j/i]-g[w][i-1]);
}
for (int i=1;i<=m+1;i++) f[0][i]*=D,g[0][i]*=D;
rt=0;
for (ll i=1;n/i>m;i++) {
for (int w=0;w<4;w++) rt+=(f[w][i]-g[w][m]);
//cout<<"H"<<rt<<endl;
}
return rt;
}
int main()
{
//freopen("input.txt","r",stdin);
ll n; cin >> n >> A >> B >> C >> D;
ans=solve(n);
for (ll i=2;i<=m;i++){
if (is_prime(i)){
res=A*i*i*i+B*i*i+C*i+D; tmp=n;
while (tmp){
ans+=res*(tmp/i);
tmp/=i;
}
}
}
cout << ans << endl;
return 0;
}
#include <bits/stdc++.h>
using namespace std;
const int MAX = 1e5 + 10;
bool black[MAX]; // is it vertex black now
vector<int> vec[MAX]; // main edges
bool old_black[MAX]; // to remember the tree before block
const int MAX_BLOCK_SIZE = 600;
int t[MAX], v[MAX]; // queries
bool used[MAX]; // is in mini-tree
vector<pair<pair<int, int>, int> > v2[MAX]; // mini-tree edges (son, number of white vertices, dist)
int push[MAX]; // push of the i-th vertex in mini-tree
bool clear[MAX]; // do we need to clear first
void dfs_1(int pos, int prev = -1, int white = 0, int dist = 0){
if(used[pos]){
if(prev != -1){
v2[prev].push_back(make_pair(make_pair(pos, white), dist));
}
for(int a : vec[pos]){
dfs_1(a, pos, 0, 0);
}
}else{
if(!black[pos]){
white++;
}
for(int a : vec[pos]){
dfs_1(a, prev, white, dist + 1);
}
}
}
void make_1(int pos){
if(!black[pos]){
black[pos] = true;
return;
}
push[pos]++;
for(auto a : v2[pos]){
if(a.first.second + 1 <= push[pos]){
make_1(a.first.first);
}
}
}
void make_2(int pos){
black[pos] = false;
push[pos] = 0;
clear[pos] = true;
for(auto &a : v2[pos]){
a.first.second = a.second;
make_2(a.first.first);
}
}
void dfs_2(int pos, int p = 0, bool cl = false){
if(used[pos]){
p = push[pos];
cl |= clear[pos];
}else{
black[pos] = old_black[pos];
if(cl){
black[pos] = false;
}
if(!black[pos] && p){
black[pos] = true;
p--;
}
}
for(int a : vec[pos]){
dfs_2(a, p, cl);
}
}
int main(){
ios_base::sync_with_stdio();
cin.tie(0);
cout.tie(0);
int n, q;
cin >> n >> q;
for(int i = 2; i <= n; i++){
int a;
cin >> a;
vec[a].push_back(i);
}
for(int i = 1; i <= q; i++){
cin >> t[i] >> v[i];
}
int root = 1;
for(int i = 1; i <= q; i += MAX_BLOCK_SIZE){
for(int j = 1; j <= n; j++){
used[j] = false;
v2[j].clear();
old_black[j] = black[j];
push[j] = 0;
clear[j] = false;
}
for(int j = 0; j < MAX_BLOCK_SIZE && i + j <= q; j++){
used[v[i + j]] = true;
}
dfs_1(root);
for(int j = 0; j < MAX_BLOCK_SIZE && i + j <= q; j++){
int t = ::t[i + j];
int v = ::v[i + j];
if(t == 1){
make_1(v);
}else if(t == 2){
make_2(v);
}else{
cout << (black[v] ? "black" : "white") << "\n";
}
}
dfs_2(root);
}
return 0;
}
#include <bits/stdc++.h>
using namespace std;
#define MAXN 200000
#define MOD 998244353
#define rint register int
inline int rf(){int r;int s=0,c;for(;!isdigit(c=getchar());s=c);for(r=c^48;isdigit(c=getchar());(r*=10)+=c^48);return s^45?r:-r;}
int n, m, q, B, C, T, fac[MAXN+5], efac[MAXN+5], Ans[MAXN+5], A[MAXN+5], t[MAXN+5], c[MAXN+5];
int mp[MAXN+5], rv[480], h[480][100032], _init[MAXN+5], d[105][100032]; bitset<100032> b[480];
typedef pair<int,int> pii; pii S[MAXN+5]; struct QU{int u,l,r,k,i;}Q[MAXN+5];
inline bool cmpi(const QU &a, const QU &b)
{
return a.i<b.i;
}
inline bool cmpm(const QU &a, const QU &b)
{
return a.u^b.u?a.u<b.u:a.u&1?a.r<b.r:a.r>b.r;
}
//fastpow
inline int fxp(int s, int n=MOD-2){int a=1;for(;n;n&1?a=1ll*a*s%MOD:0,s=1ll*s*s%MOD,n>>=1);return a;}
inline void Init(int k)
{
if(_init[k]) return;
_init[k] = ++C;
int *D = d[C], s = 1ll*m*k%MOD;
D[0] = 1;
for(rint i = 1; i <= n; i++)
D[i] = 1ll*D[i-1]*(s+i)%MOD;
}
inline int dxp(int a, int b)
{
return 1ll*fac[a]*efac[a-b]%MOD;
}
inline int DXP(int k, int l)
{
return d[_init[k]][l];
}
void insert(int x)
{
--h[t[x]][c[x]++];
++h[t[x]][c[x]];
S[++T] = pii(t[x],c[x]);
}
void erase(int x)
{
--h[t[x]][c[x]--];
++h[t[x]][c[x]];
S[++T] = pii(t[x],c[x]);
}
inline int calc(int k)
{
int _ = T; T = 0;
for(rint i = 1; i <= _; i++)
if(!b[S[i].first][S[i].second]&&h[S[i].first][S[i].second])
S[++T] = S[i], b[S[i].first][S[i].second] = 1;
int Ans = 1;
for(rint i = 1; i <= T; i++)
{
b[S[i].first][S[i].second] = 0;
Ans = 1ll*Ans*fxp(dxp(rv[S[i].first]+k,S[i].second),h[S[i].first][S[i].second])%MOD;
}
return Ans;
}
int main()
{
n = MAXN;
for(rint i = fac[0] = 1; i <= n; i++)
fac[i] = 1ll*i*fac[i-1]%MOD;
efac[n] = fxp(fac[n]);
for(rint i = n; i; i--)
efac[i-1] = 1ll*i*efac[i]%MOD;
n = rf();
m = rf();
q = rf();
B = n/sqrt(q*2/3)+1;
for(rint i = 1; i <= n; i++)
++t[A[i]=rf()];
for(rint i = 1, c = 0; i <= n; i++)
mp[t[A[i]]]?:rv[mp[t[A[i]]]=++c]=t[A[i]];
for(rint i = 1; i <= m; i++)
t[i] = mp[t[i]];
for(rint i = 1, l, r, k; i <= q; i++)
{
l = rf();
r = rf();
k = rf();
Init(k);
Q[i] = {~-l/B,l,r,k,i};
}
sort(Q+1,Q+q+1,cmpm);
for(rint i = 1; i <= n; i++)
++h[t[A[i]]][0];
for(rint i = 1, l = 1, r = 0; i <= q; i++)
{
for(; l > Q[i].l; insert(A[--l]));
for(; r < Q[i].r; insert(A[++r]));
for(; l < Q[i].l; erase(A[l++]));
for(; r > Q[i].r; erase(A[r--]));
Ans[Q[i].i] = calc(Q[i].k);
}
sort(Q+1,Q+q+1,cmpi);
for(rint i = 1; i <= q; i++)
printf("%d\n",1ll*DXP(Q[i].k,n-(Q[i].r-Q[i].l+1))*Ans[i]%MOD);
return 0;
}
#pragma comment(linker, "/STACK:512000000")
#include <bits/stdc++.h>
using namespace std;
#define all(a) a.begin(), a.end()
typedef long long li;
typedef long double ld;
void solve(__attribute__((unused)) bool);
void precalc();
clock_t start;
#define FILENAME ""
int main() {
#ifdef AIM
string s = FILENAME;
// assert(!s.empty());
freopen("/home/alexandero/ClionProjects/cryptozoology/input.txt", "r", stdin);
//freopen("/home/alexandero/ClionProjects/cryptozoology/output.txt", "w", stdout);
#else
// freopen(FILENAME ".in", "r", stdin);
// freopen(FILENAME ".out", "w", stdout);
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
#endif
start = clock();
int t = 1;
#ifndef AIM
cout.sync_with_stdio(0);
cin.tie(0);
#endif
precalc();
cout.precision(10);
cout << fixed;
//cin >> t;
int testNum = 1;
while (t--) {
//cout << "Case #" << testNum++ << ": ";
solve(true);
}
cout.flush();
#ifdef AIM1
while (true) {
solve(false);
}
#endif
#ifdef AIM
cout.flush();
auto end = clock();
usleep(10000);
print_stats(end - start);
usleep(10000);
#endif
return 0;
}
template<typename T>
T binpow(T q, T w, T mod) {
if (!w)
return 1 % mod;
if (w & 1)
return q * 1LL * binpow(q, w - 1, mod) % mod;
return binpow(q * 1LL * q % mod, w / 2, mod);
}
template<typename T>
T gcd(T q, T w) {
while (w) {
q %= w;
swap(q, w);
}
return q;
}
template<typename T>
T lcm(T q, T w) {
return q / gcd(q, w) * w;
}
template <typename T>
void make_unique(vector<T>& a) {
sort(all(a));
a.erase(unique(all(a)), a.end());
}
template<typename T>
void relax_min(T& cur, T val) {
cur = min(cur, val);
}
template<typename T>
void relax_max(T& cur, T val) {
cur = max(cur, val);
}
void precalc() {
}
#define int li
const int mod = 998244353;
struct Query {
int l, r, id;
};
vector<int> res;
vector<int> a;
int n;
int TIMER = 0;
const int C = 200500;
int used[C];
int cur_cnt[C];
int rev[C];
map<int, vector<int>> down;
vector<int> init;
void kill(vector<Query>& all_q, int block_size, int k) {
vector<vector<Query>> by_block(n / block_size + 1);
for (auto& cur_q : all_q) {
by_block[cur_q.l / block_size].push_back(cur_q);
}
for (int i = 0; i < by_block.size(); ++i) {
++TIMER;
auto& q = by_block[i];
sort(all(q), [&] (const Query& o1, const Query& o2) {
return o1.r < o2.r;
});
int cur_l = min(n, (i + 1) * block_size);
int cur_r = cur_l;
int cur_prod = 1;
auto add_item = [&] (int val) {
if (used[val] != TIMER) {
used[val] = TIMER;
cur_cnt[val] = 0;
}
int cur_k = k + init[val];
++cur_cnt[val];
cur_prod = cur_prod * (cur_k - cur_cnt[val] + 1) % mod;
};
auto remove_item = [&] (int val) {
int cur_k = k + init[val];
cur_prod = cur_prod * rev[cur_k - cur_cnt[val] + 1] % mod;
--cur_cnt[val];
};
for (auto& cur_q : q) {
while (cur_r < cur_q.r) {
add_item(a[cur_r++]);
}
while (cur_l > cur_q.l) {
add_item(a[--cur_l]);
}
while (cur_r > cur_q.r) {
remove_item(a[--cur_r]);
}
while (cur_l < cur_q.l) {
remove_item(a[cur_l++]);
}
res[cur_q.id] = cur_prod * down[k][n - cur_q.r + cur_q.l] % mod;
}
}
}
void solve(__attribute__((unused)) bool read) {
for (int i = 1; i < C; ++i) {
rev[i] = binpow(i, mod - 2, mod);
}
int m, Q;
//read = false;
if (read) {
cin >> n >> m >> Q;
} else {
n = 50000;
m = 100000;
Q = 50000;
}
a.resize(n);
init.assign(m, 0);
for (int i = 0; i < n; ++i) {
if (read) {
cin >> a[i];
--a[i];
} else {
a[i] = rand() % m;
}
++init[a[i]];
}
map<int, vector<Query>> q;
for (int i = 0; i < Q; ++i) {
int l, r, k;
if (read) {
cin >> l >> r >> k;
} else {
do {
l = rand() % n + 1;
r = rand() % n + 1;
} while (l > r);
k = rand() % 100;
}
--l;
q[k].push_back({l, r, i});
down[k] = vector<int>();
}
res.assign(Q, 0);
for (auto& item : down) {
int init_val = (item.first * m) % mod;
auto& vec = item.second;
vec.assign(n + 1, 1);
for (int i = 1; i < vec.size(); ++i) {
vec[i] = vec[i - 1] * (init_val + i) % mod;
}
}
for (auto& item : q) {
int k = item.first;
auto& cur_q = item.second;
int block_size = std::max((int)(n / sqrt((int)cur_q.size())), 1LL);
kill(cur_q, block_size, k);
}
for (int i = 0; i < Q; ++i) {
cout << res[i] << "\n";
}
}
Bonus Problem
It is the previous D1E and its standard solution is hacked. Can you solve it?
Legend
How can the man in the high castle, Abendsen, escape so many times? Because he has a full plan of escaping —— with his films.
The map of the cities can be described as a tree (i.e. connected graph with n vertices and n - 1 edges) rooted at node 1 —— where Abenden lives.
When he starts his escaping, he plans at most k travels: one travel is a simple path between two (not necessarily different) vertices. So he goes from 1 to some vertex v1, and then goes from v1 to v2, and so on ...
When he is visiting a vertex (even though he has visited this vertex before) he will get some films. But in some vertexes, he has to give some films. Note that Abendsen \textbf{can} have a negative amount of films. But after every travel, he has to have a non-negative amount of films. Note that when Abendsen is starting a new travel, he is visiting the starting vertex too. It sounds weird but it is a different world!
At first, Abendsen does not have any films.
He wants to maximize the number of the films he gets after the escape. So please help him find out the maximized films number he can get.
Input Format
The first line two contains two integers n and k (1 ≤ n ≤ 1000, 1 ≤ k ≤ 106) —— the number of vertices and the maximum number of travels allowed.
The second line contains n integers w1, w2, ..., wn (|wi| ≤ 108) —— how many films will Abendsen get (or give if wi is negative) if he visits the i-th vertex.
Each of the next n - 1 lines contains two integers ui and vi (1 ≤ ui, vi ≤ n, ui ≠ vi) —— vertices connected by the i-th edge.
It is guaranteed that the input data describes a correct tree.
Output Format
Print one integer, the maximum number of films he can get.










Can someone explain the technique used to hash the convex hull in this solution? http://codeforces.me/contest/1017/submission/41357754
Just because I didn't come up with the idea of doubling the sequence of A (dA) and running KMP...
At first I thought of multiplying all of these lengths and angles. However, this is obviously incorrect; considering that the multiplication of these numbers can be very large, I used logarithm to convert multiplications into additions.
In this solution len[i] is the i-th length and rot[i] is the i-th angle (rotation), and these two numbers are correlated. I thought that it's hard that hashes log(len+rot) collide (this implements the multiplication of (len[i]*233+rot[i])), so... that's my solution.
More specifically, if the two convex hulls don't match, there must be some pairs of data (length, rotation) differ. While pair (length, rotation) changes, hash value (len*233+rot) changes.
Now I'm working on implementation without doubles :-)
Can someone prove why for a unique permutation of hash values (len[i]*233+rot[i])), only one polygon is possible?
Suppose W, X, Y, Z are hash values of a particular quadrilateral, then prove that there cannot be a quadrilateral with hash values Y, X, W, Z.
So here is my solution without doubles. It uses another hash function but works as well. 41434197 I just have such struct:
And then this hash function:
Where
Works pretty good.
Auto comment: topic has been updated by Magolor (previous revision, new revision, compare).
Problem F can be solved by precalc answer for n, which are divided by X, where X ~ 200000.
That is how I did it (41368570). I was very surprised when the other solution in my room wasn't this, since I thought the memory limit was way tighter than it was :P
for problem C, why does L=⌊√n⌋ always work? I eventually used that result but only from intuition and writing examples in the paper.. Does L=⌈√n⌉ not work?
nevermind, got it!
Can you explain the solution , I did not get what the editorial said.
Can you explain it to me?
This theorem states that any permutation of a sequence with at least (x-1)^2+1 distinct elements have an increasing/decreasing subsequence of length x. Take any input n and find maximum x such that (x-1)^2+1 <= n, you'll find that ⌊√n⌋ always works. So, just assume LIS (could be LDS) to be ⌊√n⌋ and build the permutation in such a way that minimizes LDS, this lead to the small increasing chunks construction and thus to LDS=n/⌊√n⌋.
I am not able to get the part where you say "⌊√n⌋ will always work". Please be more verbose about it.
These are the questions I have in mind for your second statement : 1. Take any input n , this is perhaps the length of the permutation, If I am correct ? 2. How will I find the maximum x such that (x-1)^2+1 <= n ? 3. How does the conclusion '⌊√n⌋ always works' is related to the previous findings related to x. Should x be ⌊√n⌋ ?
I am not able to figure out the concept as whole, little hints might help.
yes
just try every x=1...+inf . You will see that the maximum x you can use is sqrt(n). Take n=9, for example, (3-1)^2+1 <= 9 is valid (x=3), but (4-1)^2+1 <= 9 is not (as with any other x>3).
yes, x=⌊√n⌋
If any permutation we make has an increasing or decreasing subsequence of size x (from the theorem) and you have found x=⌊√n⌋, then you know that any permutation you build will have either LIS=⌊√n⌋ or LDS=⌊√n⌋. So just assume one, LIS for example, and make the permutation in such a way that LDS is also minimal.
Sorry if I can't make it more clear.
If LIS is ⌊√n⌋ and we make little chunks of it , as shown in the editorial for example 22 , then LDS would be n/ ⌊√n⌋ . If I am correct ? The question was a very intuitive one , if someone who did not know the theorem already
Another approach for problem F: 41353364
Find all the primes up to and then, using those primes, run the sieve in blocks of size M (here M = 8·220). Even without using bitsets, you can achieve under 1MB of memory usage without sacrificing much of the speed.
and then, using those primes, run the sieve in blocks of size M (here M = 8·220). Even without using bitsets, you can achieve under 1MB of memory usage without sacrificing much of the speed.
Another approach for problem D : 41362569
I converted 01 string in binary.
There are atmax 2n (4096) distinct 01 strings stored count of all of them in an array.
Whenever a query is made I first checked this String is already processed.
If no then calculated answers for all values of K in O(n * 2n)
Worst case Time Complexity O(n * 4n) ~ (Edit) (2e8).
That's 2e8 actually :D
Thanks. Updated.
I don't like the question F to limit my memory use. in fact, I get the answer quickly, but I spent all of my time until the contest end. If we match for algorithm, why limit others?
There is also a
O(2^(2N))solution for D which worked for the given constraints (perhaps even better than the provided solution?), by simply pre-calculating all (s,t) wu results.Checkout my comment above. Sol : 41362569 Extra n in complexity is included to account for time taken to match two strings. I didn't pre processed but evaluted when only needed.
You code may be faster if you replace map with binary search and sort.
I haven't used map. I'm using array with index as no. as val. So there is no need to sort it also.
aryanc403 I have also done the same thing but I get TLE, can you tell how to improve it. I precalculate the result for all (s,t) pairs 84729180 .
its never supposed to be. At least i can't pass........
My first submission should be a WA (by simply mistake) but not a TLE
Solution for G?
I was thinking of a HLD solution
initialize all nodes with -1.
query 1, add 1 to that node
query 2. make value of all nodes in the subtree -1.Also if query 3 on this node gives non negative value, add -1*(ans to query 3)-1 to the node
query 3. find max non empty suffix sum from that element to root. if negative , white otherwise black.
Can someone validate??
It's correct
Does this mean that you take all positive values on the chains up to root?
I would like to understand the HLD solution.
Could someone tell me why we should maintain segment-tree like this: mx[v] = max(mx[v<<1^1], sm[v<<1^1] + mx[v<<1]);? This bothered me for a day.
I think I see. This can help to maintain max suffix sum.
How do you make values of all nodes in subtree of a vertex in HLD?
HLD is also a Euler tour.
Don't understand you. As I assume, HLD is a set of paths with a data structure built on each. What does it have to do with Euler tour? Elaborate pls.
Check Here
Wow. Thanks!
Tnx for the great contest Magolor
how to solve G ?!
is it a HLD problem ?
Could somebody point out to me why this 41374761 gives TLE? Isn't its complexity: (2^n * (2^n + 100) + q * n)?
Your soln — 41375264 . I have replaced n with 15 . It gives AC because
Time take to compare i with constant (15) is less that variabe(n)Thank you. But shouldn't such complexity pass easily in 2 seconds? what's the difference between my solution and 41356297 The 2 codes are almost identical. Edit: Also seems like it only passed by luck. I resubmitted the exact code you got AC with (with replacement of variable (n) with 15) and I got TLE 41377553
As I have mentioned in my comments above. Time complexity is O(n * 4n). For n=12. This is around 2e8. Hence It just passes TL. There are some highly optimised solns with this time complexity which takes around 500 ms.
No, it shouldn't. It is actually living on the edge.
But if you used bitmasks/BITSET I think you can cut down runtime dramatically.
I did use bitmasks. What confuses me the most is that after the contest I got inspired by this 41356297 submission and my 41374761 submission are almost identical except for maybe using vectors instead of arrays. but the AC solution passes in 1300 ms and mine can't run below 2s :/ I really can't spot the difference between the 2 codes.
Try to only run the dp when necessary (whenever you encounter a new mask) and keep track of whichs masks you've seen. It should now cut it to something like a bit over 1 second.
I've seen that in other solutions but it's really bothering me how the AC solution 41356297 — which I almost copied — still runs in below 1.3s without having to do that. What's the key for the quick runtime there?
Speedups/observation:
Arrays vs Vectors (arrays faster)
Array Indexing:
Basically if you look at his code all of the index sizes are increasing order. This actually can run way faster (something with memory access)
It seems making V a global variable (outside of main) is a big speedup, not sure why though.
UPD1: http://codeforces.me/contest/1017/submission/41379154
Got it to pass by using more arrays instead of vectors, increasing index, and making 'v' a global variable.
This is still far from 1200 ms though.
UPD2: Found the culprit. You use endl instead of '\n' which is slower becaus it does extra stuff.
Your code is actually way faster lol: http://codeforces.me/contest/1017/submission/41379280
Thank you very much for your effort. Much appreciated and noted these things down! never using endl; again! :D
You can use
#define endl '\n'for that.It's because you use
cout << ... << endl;.endlis a newline and a flush; it's the same ascout << ... << '\n' << flush;. In other words, your code is attempting to write to disk 500,000 times, which is not going to finish in 2 seconds.Waw, thanks so much!
In C, why is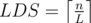 minimal for a given LIS = L?
minimal for a given LIS = L?
Because you can order the array in L chunks. Depending on if the elements within the chunk are increasing or decreasing, the i'th element of some chunk will be strictly less then or greater than the i'th element of the next chunk.
So if LIS or LDS is L (amount of chunks), the other N/L (size of chunk)
Example: 1 2 3 4 5 6, L = 2
{4 5 6 } {1 2 3}
4 > 1, 5 > 2, 6 > 3, so it can be clear LDS = 2
4 < 5 < 6, and 1 < 2 < 3 so the LIS = 3
Thanks, the algorithm is clear (I solved the problem exactly this way), but I actually asked a different question. I was wondering how to prove that one cannot construct a permutation with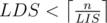 .
.
Oh, I am sorry for restating the obvious.
Here it is:
([x] is a sequence of x increasing numbers)
LDS is the amount of chunks [LIS][LIS][LIS]...[< LIS]
As you can see, the amount of chunks is the LDS, and here the amount of chunks is (amount of [LIS] chunks) + 1
Amount of [LIS] chunks is "how many LIS fit into N" which is floor(N/LIS), and we also add 1 to include the smaller leftover chunk.
Among the integers, floor(x)+1 = ceil(x)
So it's ceil(N/LIS).
Now imagine it is a perfect square. Then rounding doesn't matter.
Hope this helps.
I think that what he need is a proof of the optimality, but you just provide an algorithm and calculate the [LIS]+[LDS] without proving that this algorithm is optimal.
Assume a permutation with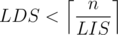 exists. Assign pairs
exists. Assign pairs 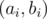 to all elements such that ai denotes the length of a LIS and bi denotes the length of a LDS ending at position i. It follows that all pairs must be different (why?) and we have
to all elements such that ai denotes the length of a LIS and bi denotes the length of a LDS ending at position i. It follows that all pairs must be different (why?) and we have
as well as
Thus, there are less than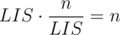 pairs and two of them must be equal by pigeonhole principle. Contradiction.
pairs and two of them must be equal by pigeonhole principle. Contradiction.
Note: This is the same proof idea used in Erdős–Szekeres theorem.
This is brilliant. Can't thank you enough!
and (how, why)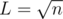 always work ?
always work ?
This problem basically simplifies to a much easier problem because A*B = N (you must use all elements 1 to N).
So imagine you have a number N and you want to minimize A + B where A*B = N.
Actually in this case A = B = sqrt(N).
For example:
A,B values for 16
(1,16) (2,8) (4, 4)
The best A,B is in the "middle" of the factors, which is sqrtN.
how you convert the problem from A + B to A × B ?
We want to minimize (A+B) so that A*B = n.
So for 16, the minimum A+B = 8, because we have A = 4, B = 4, and 4*4 = 16.
yes, why ?!!
https://codeforces.me/blog/entry/61061?#comment-450032
Look at the problem discussion. I'm sorry but I can't say much more than "drawing it out".
You will notice that if you split it into K blocks (with increasing values between blocks) you will notice a LIS is contained within block while LDS is contained across the blocks. (or other way around, either is fine)
7 8 9 ||| 4 5 6 ||| 1 2 3
thanks so much, now i understand somehow
Why A*B=N ?
I can’t get it.(sad)
Actually, since we have to minimize L + ceil(n/L) (L = length of the LIS)
So, we have to minimize f(x) = x + ceil(n/x) or simply minimize x + n/x
Find out it's minima point by differentiation of f(x)
On solving we get x = sqrt(n).
We want to make a permutation of size N, so we can use divide our answer into A increasing blocks of size B. A*B must equal N to use every single numbers from 1 to N.
In problem C, how does Dilworth's theorem relate to LIS and LDS in a permutation?
I have the same question!
Trying to understand the relationship between LIS and LDS with Dilwort's theorem I found this paper (http://math.mit.edu/~cb_lee/18.318/lecture8.pdf).
Theorem (Dilworth 1950): Let P be a poset. Then there exists an an-tichain A and a chain decomposition C satisfying |C|=|A|.
Someone can explain the relationship between the theorem, LIS and LDS?
What is an an-tichain A and what is chain decomposition , sounds greek to , can some one please care to explain , if they are related to problem c.
I think I got it.
Let's assume that we are given some permutation of numbers 1 ... N.
Then let's define a relation
i«j
as "i is smaller than j and it occurs earlier in the given ordering".
Then we apply the Dilworth theorem in terms of this relation. A longest antichain corresponds to the longest decreasing subsequence. If LDS has length L then by the theorem statement we know that the partially ordered set cannot be partitioned into fewer than L chains. Chanis correspond to increasing subsequences and thus LIS cannot be shorter than ceil(N/L).
We are supposed to come up with the construction algorithm and the Dilworth theorem helps prove that it matches the lower bound for LDS+LIS.
IMO this problem was more difficult than its score! :\
Problem C
Looking at Erdos lap number the other day and came through this theorem.
https://en.wikipedia.org/wiki/Erd%C5%91s%E2%80%93Szekeres_theorem Edros Theorem says any permutation of n^2 + 1 distinct numbers has a increasing/decreasing sub sequence of n+1.
And one more solution for D: 41376803 It has O(22n + q * n) complexity and the most interesting part — it doesn't use that k is relatively small.
First, as in mouse_wireless's solution, we want to count Wu value for all possible masks and create a vector prew containing pairs (Wuvalue, mask). Then we sort this vector in increasing order and now we are ready to another precalc)
For each possible string t we build a vector based on prev: we just change mask to ( ), which will represent s string needed to get this mask. Now we have to iterate over new vector once again to do following: we will change second value in every pair (ex-mask and ex-(
), which will represent s string needed to get this mask. Now we have to iterate over new vector once again to do following: we will change second value in every pair (ex-mask and ex-( )) to number of string in S, for which Wuvalue doesn't exceed current Wuvalue (in current pair). We can do this by simple dp.
)) to number of string in S, for which Wuvalue doesn't exceed current Wuvalue (in current pair). We can do this by simple dp.
Now, for answering a query, all we need is binary search a vector related to given t. It is the part which has a O(q * n) complexity.
Unfortunately, during the contest I got TL4 with this solution beacause of slow IO. Thanks to SHAMPINION, who advised me to add two stirngs of code, which make IO faster and after that the solution passed in 1.7 s.
I had a similar solution to D, with two differences:
1) Rather than sort the list of (Wuvalue, mask) tuples, it's actually possible to use a Dijkstra-like approach to save a sorting step. This is only a minor speedup though, since computing this list only needs to be done once.
2) Rather than use binary search, I sorted the queries by k and then iterated in order of increasing Wuvalue's and k's. This saves quite a bit of memory, since you don't have to memoize the results.
AC in 607ms! 41379365
In problem E, I have understood that after getting the hulls of the 2 engines, we will represent each hull using a string of edge lengths and angles. After this, Double one of the two strings, and then check that the string which is not doubled exists in the doubled string.
Edge lengths would not change between 2 isomorphic hulls, but angles could change. So, how to normalize angles of the two hulls such that their KMP matching becomes rotation invariant?
EDIT: Never mind, I got it.
For problem E, Magolor's solution differs from Kostroma's solution in this input:
Output should be "No", since reflection is not allowed.
For 1017E - Сверхзвуковая ракета, many of the accepted submissions (around one-third?) actually fail on this test case:
I wrote up a detailed explanation of what's going on in this post: https://codeforces.me/blog/entry/61086
Can we add this case to the practice version of the problem?
EDIT: Looks like ivanzuki above has the same idea and I was a bit slow. That's what I get for writing a long post :)
For problem D,I use O(q × 2n) "solution" and passed it.
my code:http://codeforces.me/contest/1017/submission/41379865
Can you explain your solution please? And also I cannot view the code and I don't know why.
Now you can read it.
I think that Problem F can also be dealt with easily should one know about the technique of Extended Eratosthenes Sieve.
That is, we can even solve the problem for n ≤ 1011 without the memory limit. :)
My code: 41366266
By the way, Problem E can also be done by finding the minimal string rotation of two convex hulls and compare them with brute force.
Please briefly explained problem B.
Do you understand the problem statement? Let everyone know and we may have further explanation.
Yes but I couldn't understand the solution in tutorial.
Let me explain an intuitive and naive solution this way.
There are some notes:
ORoperator (assume it isA | B = C) will make the result become1ifAorBis1or bothAandBare1.Look at these two binary numbers:
Notice that, in each column of the representation of the two numbers above, if you make a pair of one element from number A and one from B, you will have these "vertical" pairs:
00,01,10,11(assigning namesp00,p01,p10,p11)The first digit in each pair comes from
A, and the second digit in each pair comes fromB.Because the problem is about swapping two different elements in
Aso that it makes change whenORis done, in each pair above, the first digit will be the one which is swapped with another first digit in another pair, and the second digit will stay still.Also by the notes, when we make a change (i.e. a swap of two different elements in
A), the one digit we take has to be different from the other digit we take to perform the swap, otherwise the swap become nonsensical because no any elements are changed. In another word, for a pair of positions, there must be a pair of different elements inA, or bothAandB. So we can say that the swap for thesepmake sense:p00withp10p00withp11p01withp10p01withp11p10withp00p10withp01p11withp00p11withp01Notice that we have to put each
pvertically in actual representation.Look more closely at such pairings above, by notes again, we notice something redundant in some pairs:
p00withp10(OK:OR=01before &10after swap)p00withp11(OK:OR=01before &11after swap)p01withp10(OK:OR=11before &10after swap)p01withp11(NO:OR=11both before & after swap -> no change)p10withp00(OK: Same as the first one)p10withp01(OK: Same as the third one)p11withp00(OK: Same as the second one)p11withp01(NO: Same as the fourth one)Now that we get these pairs left and they are OK:
p00withp10p00withp11p01withp10Therefore the result as shown by the tutorial writer.
I hope this would help you.
Sorry for my
English because this may not such a long explanation like this.Thanks for your very good explanation ....
I came up with the solution of A~G but I made mistakes in my segment tree and failed to pass G...
My solution of problem D~G:
D:
Let f(i, s, k) be how many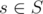 can be gotten by changing s[i, n) with a cost not greater than k.
can be gotten by changing s[i, n) with a cost not greater than k.
When k < 0, f(i, s, k) = 0, otherwise:
f(n, s, k) is the count of s in S;
When i < n,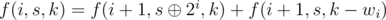 .
.
The answer of a question is f(0, t, k).
Complexity: O(2nnk).
E:
The problem is equivalent to checking if two point sets' convex hull is the same by shifting and rotating one of them.
If two convex hulls' size are different, the answer is NO. Otherwise, let k be their size, and number the points of each convex hull 0, 1, ..., k - 1 clockwise. Let Pi be point i in the first convex hull and Qi be point j in the second convex hull.
Enumerate which point Qi is corresponding to point P0, and check if for each j = 0, 1, ..., k - 1:
The answer is YES if and only if there is an i satisfying this condition.
To avoid floating point operations, we use
instead of $\lvert P_{i}P_j\rvert$ and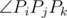 , among them Pi(xi, yi). The absolute value of these numbers are not greater than 2 × 1016, we can use 64-bit integer to store them.
, among them Pi(xi, yi). The absolute value of these numbers are not greater than 2 × 1016, we can use 64-bit integer to store them.
I use string hash to solve it. Initialize the prefix and suffix hash value of sequence
Then checking one i costs O(1) time.
After calculating the convex hulls, the complexity is O(n). The total complexity is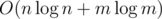 .
.
F:
Let P = {p1, p2, ...} be the prime set(pi < pi + 1). The answer is
When $p\le\sqrt{n}$, we can calculate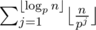 by brute force.
by brute force.
When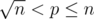 ,
, 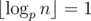 , so now we need to calculate
, so now we need to calculate 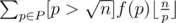 .
.
Consider Eratosthenes sieve, let f(n, m, k) be the sum of k-th power of the rest numbers after deleting all pix (i ≤ m,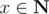 , x > 1) from 2, 3, ..., n, while 0 ≤ k ≤ 3.
, x > 1) from 2, 3, ..., n, while 0 ≤ k ≤ 3.
Obviously,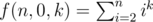 , it can be calculated in O(1) time.
, it can be calculated in O(1) time.
If pm2 > n, f(n, m, k) = f(n, m - 1, k).
Else,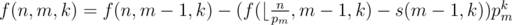 ,
, 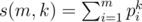 .
.
Then we can get the sum of k-th power of the primes in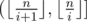 , it's
, it's 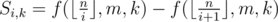 (pm2 > n). Summing
(pm2 > n). Summing 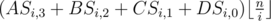 up and we can get the answer.
up and we can get the answer.
Because the first parameter is always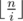 ,
,  , and pm2 ≤ n, the time complexity of calculating f is
, and pm2 ≤ n, the time complexity of calculating f is 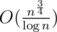 . Scrolling the array can optimize the memory.
. Scrolling the array can optimize the memory.
Time complexity: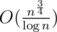 .
.
Memory complexity: .
.
G:
Let f(v) be how many operations 1 are operated on vertex v, then f(v) = max{f(pv) - 1, 0} + c(v), c(v) is the count of direct operation on v, i.e. "1 v".
If f(v) > 0, v is black, otherwise v is white.
We can use heavy-light decomposition and segment tree to maintain f. Consider a chain 0 - 1 - 2 - ... - n, if the status of 1, 2, ..., n is known, f(n) can be described as a function of f(0): f(n) = max{f(0) + a, b}. When using segment tree to maintain the heavy-light decomposition, each node storages the a, b of its interval. Then for an operation "3 v", we can query the value of f(v) in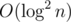 time.
time.
For single vertex v (leaves of the segment tree), at first its a = - 1, b = 0. After an opeartion "1 v", increases its a, b by 1.
After an operation "2 v", decreases v's a, b by f(v) (current value), and restore the subtree v (not contain v) to a = - 1, b = 0. Because the value of f(v) is increasing before restoring, this algorithm is correct.
Complexity: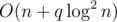 .
.
UPD: H can be solved simply by Mo's algorithm, but I didn't open this problem at all...
What is Dilworth's Theorem? How do I learn it? Do I need to know anything else before learning it?
https://www.youtube.com/watch?v=S8mXDhGs_pg It's from Codechef's Indian Programming Camp 2016. This might help you learn it if you want to start from scratch.
This helped to understand the actual explanation of the approach used. Thanks.
Another simple way to check convex hull isomorphism in problem E is to simply check the relations between consecutive triplets of points (as if you are checking triangles congruency). In this way, angles will be implicitly considered.
This code is not O(N^2), because matches between triplets cannot be dense, and the inner loop will not take so long before it breaks. However, I couldn't formally prove it.
Edit: From the reply of Kostroma
This code is O(N*M), where M is the maximal number of equal edges in a convex polygon, which can't be that big due to the constrains on the coordinates.
Here is my accepted submission: 41392476
actually the convex hull with integer points will only have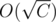 in size, so the complexity of checking the same would be O(C)
in size, so the complexity of checking the same would be O(C)
I am really interested in this conclusion. Could you provide proof or more detail about it?
I learned it from a competitive programming camp.
I couldn't memorize the proof well, but it's just something like every adjacent edges won't be colinear, so there won't be too much points on the convex hull.
p.s. why downvoting me...
This code IS n^2. It's just weak tests.
Wanna give a test or just unproven cock-a-rats? I believe it works in O(n·M), where M is maximal number of equal edges in a convex polygon, which can't be that big with these constraints on coordinates surely.
Maybe I'm misunderstanding his solution, but IMO if the two polygons are the same, except one vertex, then it will have O(N^2) running time.
I think that almost all iterations of the outer loop will be short, because there can't be many long equal parts in two convex polygons with vertices in integer points.
In my understanding, his solution checks if the triangles created by 3 adjacent vertices are coincident.
If that's what it does, then by having the same polygon twice, just moving 1 vertex by a little, the inner loops running times will be 1,2,3,...,n which summed is O(N^2).
If the two polygons are the same (except for maybe one side), the inner loop will NOT be O(n) for all the iterations of the outer loop.
Because if the two polygons look similar when v1[0] corresponds to (coincides with) v2[0], it doesn't mean that they will look similar when v1[0] correspond to v2[1].
The only exception is when the two polygons are somehow close to regular polygons, as many matches will occur no matter how you rotate the polygon's vector. In this case the code will really be O(N^2). However, you cannot have a regular polygon with many sides given the constrains of the problem.
Can anyone explain the solution of problem D in the editorial? I solve D with another solution, but didn't understand the provided solution. Why f[S1][S2][j], and what is it going to do with g[S][k]?
The complexity in F is just too BS. Setting the limit of N to just 1e8 would make a lot of us see that this complexity works, but 3e8 just makes alot of people says: It's not gonna pass.
Вот бы завезли более подробный разбор на русском языке
I think problem G can be solved by using Segment Tree Beats. This is my solution: https://codeforces.me/problemset/submission/1017/41447852
Can you tell me what pii lz[N<<1] do ?
you can search info about it before asking me
each node in my segment tree doesn't maintain the value of 1 range. A node has value if only if its range is a position
Could somebody point out to me why this gives TLE? https://codeforces.me/contest/1017/submission/41443492
Failing G on test 6, but can't seem to find my bug. Could someone help? Thanks in advance!
http://codeforces.me/contest/1017/submission/41515637
UPD: Accepted.
In div2C: I want to answer why sqrt(n) will always work: I won't talk about the statement that: if lis = L then optimal lds = n/L (1) Because it has been proved severel ways. But lets for now believe the above statement(1) and use it. We know that secret_number = lis + lds = lis + n/lis. Then we have secret_number as a pure function in lis. Now we want rewrite as f(lis) = lis + n/lis Know we want to minimize the above function. In other words we need the optimal lis that minimizes f(lis). And here some calculus will answer us : differentating a function is equavelent to getting its slope of tangent to the function curve wrt to its independent variable(lis), we may notice that when a tangent to a curve is parallel to x-axis at some point x then: at this x the function is at a peek (minimum or maximum). So we set the function derivative to zero (slope is 0 when tangent is parallel to x-axis) and solve for Lis, the obtained lis is the one that minimzes the function. F'(lis) = 1 + n / (lis^2) Setting f'(lis) = 0 ===> lis = sqrt(n).
In problem E, the first official solution fails on this case:
which is actually test case #55 in the judge system (so weird).
The solution outputs YES, when the answer is NO.
This is due to all cross products of consecutive sides being the same (1 or -1), and the sequences of sides' square length are 2,1,2,1 and 1,2,1,2 respectively. So when we duplicate the second-one (without losing generality), we get 1,2,1,2,1,2,1,2 and it can be seen that it contains the first-one as a substring (starting on position 2).
I think this is because of the use of the cross product. I think dot product should be used instead, because it will characterize the angle between two consecutive sides of the hull better than the cross product, which is in fact characterizing the area of the triangle.