Given 3 points in 3D, is there a way to calculate the area of the triangle made by them in O(1), considering the Cross Product will need to use the square root to calculate the magnitude of the vector produced by the cross product?
→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 164 |
| 1 | maomao90 | 164 |
| 3 | Um_nik | 163 |
| 4 | atcoder_official | 160 |
| 5 | -is-this-fft- | 158 |
| 6 | adamant | 157 |
| 6 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 8 | nor | 154 |
| 10 | djm03178 | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 13.11.2024 05:47:45 (k1).
Десктопная версия, переключиться на мобильную.
При поддержке
There is no difference in the formula for 3D: abs(CrossProduct(P1 — P0, P2 — P0) / 2) should work again.
You need the square root function to compute the abs of the CrossProduct, isn't O(1).
I think it is impossible, because in any way you need to know the length of some vector or segment
Also if it was possible, how could we find the area of a triangle if it was of form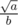
.
There is a way to do that in 2D, which is applicable for all polygons by applying the following formula to all the polygon edges:
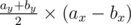
Which is O(1) for a triangle.
Imagine the points (0, 0, 0), (0, 0, 1) and (2, 1, 1). The area of the triangle, formed by them is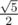
. So if there was is a formula to exactly compute the area, then it should be able to somehow compute 
.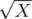