Problem was solved!
Input is consist of 1 ≤ q ≤ 2 * 104 queries every of which are described with single positive integer n not exceeding 4 * 106.
Output is to print for each query: 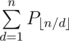
Where:
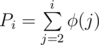
⌊x⌋ = whole part of number, i.e. max integer which's ≤ x
φ(x) is Euler Totient Function
OK, I can previously calculate phis of all numbers from 1 to 4 * 106 and Pi for any i, 1 ≤ i ≤ 4 * 106 in O(nlogn), but what's then? I don't know how to further optimize solution, because it is TLE with O(n) complexity per query.
Please, help me!











Hint: How many different possible values for floor(n / d) exist?
Not more than 2 * sqrt(N).
for each d < sqrt(n), we get two values (n / (n / d) = d, n / d)
for every value d > sqrt(n) , n / d will be less than sqrt(n), so if it is possible to obtain this value, we already obtained it when d < sqrt(n).
What next?
for each of these 2 * sqrt(n) values, find out how many times it occurs and calculate it's answer in O(1).
Wow, thank You very much, I thought it's fact only when d|n, is it so with a lot of other concepts, too? If it is, can You please provide some examples, I'm very grateful for your response.
Sorry I didn't understand what you meant by:
If you want a formal proof take a look at this
Thank You!
I meant: 'I thought there're ≤ 2sqrt(n) only divisors of n and that's the only thing which we can find in O(sqrt(n))'.
Can You please provide some other similar examples?
There are ~2sqrt(n) (the ones I mentioned) values that might be divisors for n, some of them can be actual divisors and some not, thats why there are ≤ 2sqrt(n) divisors for n.
Wonderful!
Do You think if there exists solution faster than O(qsqrt(n)logsqrt(n))? Or is it just me so silly and straightforward?
It can be done in O(Qsqrt(n)).
Let's look at n = 25
n / 1 = 25 , n / 2 = 12
So for any value d between 13 and 25, n / d would be 1. So 1 occurs (25 - 12) times.
Similarly, n / 3 = 8, so 2 occurs (12 - 8) times. And so on for all other values.
Amazing!
I thought about such approach too, but didn't get to the end.
I'd like to first implement O(Qsqrt(N)logsqrt(N)) solution. But there's one trouble...
I understood that I didn't understand nothing at all... (maybe it makes You sad too in a meaning of such waste of time on me, I'm very sorry if it is).
Can You please explain it to me one more time! And to find out gaps as fast as possible, I'll try to show You how much I didn't get.
Let n = 10
Then I just go to its root floored down -> 3
And there, I consider pairs and update their occurrences:
(1, 10)
(2, 5)
(3, 3) // but don't add second time, since they're equal
Here's what I get:
Occurrences: 1 1 1 0 1 0 0 0 0 1
___Numbers: 1 2 3 4 5 6 7 8 9 10
But result should be:
Occurrences: 10 5 3 2 2 1 1 1 1 1
____Numbers: 1 2 3 4 5 6 7 8 9 10
What I do wrong?
n = 10
the numbers that occur are 1,2,3,5,10
the number of occurrences are:
1: 10-5 = 5
2: 5-3 = 2
3: 3-2 = 1
5: 2-1 = 1
10: 1-0 = 1
Thank You very very extremely much!
I understood concept after a few hours on paper! And I finally solved it in O(Qsqrt(N) + NlogN)!
My solution: 39462553. I missed some stuff there and original problem asked to calculate
But however, by understanding concept I could further generalize it and solve, thank You very much again!
Awesome! glad I could help :D
I have a little problem that i could not solve but is related... So you have a grid of N * N and have to color some of the squares that so you have no 2, let them be (x1, y1) and (x2, y2), with proportional coordinates(x1 * k = x2, y1 * k = y2). U have to output the number of ways to color them. I think it is a real-cool problem
What is a constraint for n?
If I understood statement right, problem asks You to calculate:
doesn't it?
It can be rewritten as:
N is at maximum 12 000 000 and limit is 1 second. The site where this problem is stated gives TLE like crazy. Even the oficial solution gives TLE....
Solution is:
And this can be further optimized until O(sqrt(n)logsqrt(n)), since there are at most 2sqrt(n) unique values of n / d, among all 1 ≤ d ≤ n
You didn't understand the problem. For every (x, y) such that x is coprime with y you can only have one ore 0 of (x, y) (2 * x, 2 * y) etc.
You didn't say anything about co-primeness between x and y. If it's easier for You to speak and write in Russian, do it. I can speak Russian, too. Can You please explain to me problem's statement again, please. (if more preferable for You, in Russian). And please, give some samples with explanations, if possible.
I don't speak russian but I can provide you examples. The official statement is in mongolish. U can print the answer module 1e9 + 7. Example 1 : for n 1 the answer is 2. For n 2 example is 12. The pairs are: {}, {(1, 1)}, {(1, 1), (1, 2)}, {(1, 1), (2, 1)}, {(1, 1), (1, 2), (2, 1)}, {(2, 2)}, {(2, 2), (1, 2)}, {(2, 2), (2, 1)}, {(2, 2), (1, 2), (2, 1)}, {(1, 2)}, {(2, 1)}, {(1, 2), (2, 1)}.
Auto comment: topic has been updated by prudent (previous revision, new revision, compare).