There are q<=5*10^5 online queries of 2 types for a set of integers:
- Add an integer 1<=x<=10^9 to the set
- Remove an integer from the set
- Find the minimum element >=x that isn't present in the set
Is there a way to efficiently process these queries?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
There are q<=5*10^5 online queries of 2 types for a set of integers:
Is there a way to efficiently process these queries?
| Name |
|---|



If you can answer in offline, then just compress X in all queries and use simple segment tree with sum on a range of fenwick tree. If you must answer in online then use implicit segment tree.
Can you kindly provide more information?
And would your idea work with answering interval query?
in other words, suppose you have array of N items and Q queries and you want to find the MEX in each [L, R].
n, a[i] <= 1e5.
Come on, think before asking. I get that the comment above was terse but at least this should be clear:
If you can find the smallest element that is not in the set and is at least $$$L$$$, then of fucking course you can find the smallest element that is not in the set and is at least $$$L$$$ and at most $$$R$$$. Either the answer is the same or it doesn't exist in the second case.
Huh, I thought he was asking about a querying the MEX of a subarray, not about the problem from the blog but with ">=x" replaced by ">=x and <=y".
Oh shit, okay. In that case I'll be annoyed by asking not really relevant questions instead of not thinking.
In your previous version, you did not mention that you can remove elements.
So my approach will work when you just add elements and query.
When I am adding x to set, I will:
1. Unite the clusters of x, x-1 if x-1 is present in set
2. Unite the clusters of x,x+1 if x+1 is present in set
When doing the unite, maintain the global max of that cluster.
The ans for 2nd query will be then the global max of its cluster + 1.
You have 5 * 10^5 queries, so answer is less than 5 * 10^5. So you can make a set2, where you keep integers that are not in your set. Answer will be set2.min
Sorry if the title confused you, query 3 wants the mex >= x, where x can be anything.
a simple lower_bound on the set2 will do that...wont it?
EDIT: kinda messed up here :P....x can be large
The added elements can range from 1 to 10^9, so unless for query 3 x is always 0, set2 has to start with all integers from 1 to 10^9.
ah right...i messed up there...just use a dynamic segment tree then..
You only need to consider all numbers x and x+1 such that x is a number from the queries. So, it will work.
Oh, I missed it, sorry) So you can do smth like this with dynamic segment tree Or if your problem is offline, you can make "compressison of coordinates" and use my trick with lower_bound, If problem is online you also can do it, in this case you need to keep set of segments(if you added 1,5 and 7 to your set, your set 2 will contain (2,4), (6, 6) and (8, 10^9). Now you can do lower_bound again)
You can also maintain a dynamic segment tree on the values (x)..store frequencies of 'x' maybe even count of numbers (store 1 if frequency of 'x'>=1)...this is probably an overkill for your problem but will allow even queries like kth element >=x which isn't present in the set (do a binary search integrated in the segtree...still log(x) ). So yeah might give you little more flexibility. Might not be super good memory wise though...
Use Treap that accumulates following data:
Maintaining such a prefix isn't that challenging. If prefix of left subtree equals to size of left subtree AND maximum of left subtree + 1 equals to key of current node then the prefix of current node is prefix(left) + 1 else it's just prefix(left). If prefix(left) + 1 = prefix(this) then you should inspect the right subtree: if min(right) - 1 = key(this) then prefix(this) = prefix(left) + 1 + prefix(right).
Now to answer queries:
Given x you should split you treap by key x. Now, right tree after split contains all integers greater than x. If min(splitright) - 1 > x then the answer is just x + 1, otherwise you should split splitright by count(not key), where count = prefix(splitright). The answer will be max(split - by - countleft) + 1.
Time complexity per query(any) : O(log(Q)), Space complexity: O(Q), Q = 5 * 105.
Nonetheless, Treap is not the fastest data structure so do not expect this solution to be blazing fast.
The fastest way is Fenwick tree with length 5*10^5 (as the answer can't exceed 5*10^5).
Sorry if the title confused you, query 3 wants the mex >= x, where x can be anything.
Can you share the link of the problem from any online judge?
I think the best solution would be to have a BBST (Treap, Splay...) where each node contains the closest node with a count of 0.
When you insert a value at x, make sure to add a dummy node with count 0 at (x+1).
When you are removing, simply subtract the counts by 1.
When you are querying, first check if the query element exists. If it does not exist, then the answer is simply that, otherwise use the nodes in the tree to binary search for it.
let's say we have an ordered-set (but here we can keep frequencies in map).
Now insertion and deletion into o-set is straightforward.
For finding smallest y such that y>=x and y is not present in the o-set we can binary search on y in the range [x,infinity].
1 : it will work in O(logn)
2 : it will work in O(logn)
3 : it will work in O(logn*log(range))
Please point out if you find any mistake or flaw in the logic.
Store your current collection as a union of intervals. For example, if your actual set is S = {1,2,3,7,10,11}, store it as [1,4), [7,8), [10,12). You can easily use a standard C++ set for this.
Operation 1: Add a one-element interval [x,x+1). Check whether you need to merge it with the previous and/or next interval.
Operation 2: Using set::upper_bound, find the interval that contains your x. Remove it from the set, split it into two smaller intervals and reinsert them if they are not empty.
Operation 3: Using set::upper_bound, find whether x is in your set. If it isn't, return x. If it is, return the upper bound of the interval that contains x.
Each operation runs in O(log n) and you don't need to implement any trees.
My idea:
Create a set of intervals S. If the interval [l, r] is present in S, that means that the elements l, l + 1, l + 2, ..., r are in S. Adding an element x is handled like this: If [whatever, x - 1] is present in the set, remove it and add [whatever, x]. Likewise, if [x + 1, whatever] is in the set, remove it and add [x, whatever]. Removals are handled in this way: Find the interval containing x. Split it in two intervals [start, x - 1], and [x + 1, end]. MEX queries are handled similarly: Find the interval containing x. Output end + 1. This can be implemented using 2
std::set<std::pair<int, int>>in C++. The first set indexes pairs by the first element (i.e. left end), and the second one by their second element (i.e. right end).This gives WA in some cases. https://atcoder.jp/contests/hhkb2020/submissions/17318696 Can we do it without the use of
std::optionalas well?Indeed,
{p2->first, p1->first}should be{p1->second, p2->second}: https://atcoder.jp/contests/hhkb2020/submissions/17323306what about the
std::optional?? It is not available in c++-14You could use
std::pair<T, bool>instead ofstd::optional<T>.You can also use a bit trie — this is a trie made of bits of your numbers, thus it is represented as a binary tree (since there are only two types of bits — 0 and 1), and its depth is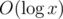 .
.
When you add a number, you mark the vertex that representing this particular number as a full binary tree, and then you recursively go over its parents marking them as full binary trees if their left and right children are both full binary trees as well.
When you remove a number, you unset the "full binary tree" mark and do so for all its parents.
When you want to get mex, you should do the DFS towards x, avoiding visiting subtrees which are marked as full (because there are no free values in such subtrees), and attempt to visit a left subtree first if you are allowed to by the x restriction.
I admit that there are better solutions above for this particular problem, but it's good to know about that function of a bit trie: for example, you can perform both "find mex" and "xor all the values" operations with a single data structure. This structure was even proposed to be implemented once on Open Olympiad (check the latest problem).
This method is really awesome.
you can use ordered set from library, it's enough for your problem
You can solve it with 2 sets. Keep one set of values that are in the set, and one set of "next values that aren't in the set". So if x is in the set and x+1 isn't in the set, x+1 is in the second set. Query can be answered by checking if x is in the first set, if it is the answer is the lower bound of the second set otherwise the answer is x.
a single treap is enough
Problem link?