Блог пользователя mayankp

IOI 2011 Elephants
Автор mayankp, история, 7 лет назад, По-английски

I have heard that the following problem that came on the 2011 IOI had a solution with O(log n) queries rather than O(sqrt(n)) queries by using link-cut trees. What is that solution?

  • Проголосовать: нравится
  • +3
  • Проголосовать: не нравится

»
7 лет назад, # |
  Проголосовать: нравится +10 Проголосовать: не нравится

Implicit treap magic. I don't remember how exactly it went, there's a comment in Russian somewhere here explaining it.

I implemented that solution a year ago, it was a fucking nightmare to get it right.

→ Ответить
  • »
    »
    7 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    Yup, I guess KOTEHOK told us this right after a contest. It goes something like this: let's take a look at the greedy algorithm. Basically, for each elephant we have a pointer to the first elephant after it which should come in the next block. This structure is a rooted tree, and answer for the problem is depth of a specific vertex in that tree. Now a modification query is something about moving vertexes in that tree. If we store that tree as an Euler tour in an implicit treap, it can be performed efficiently.

    → Ответить
    • »
      »
      »
      7 лет назад, # ^ |
      ← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

      Just to point out something nontrivial here — if we do this exactly as you said then moving one elephant may require O(n) changes of edges in that tree which is kinda troublesome. However dacin21 already explained below how to deal with this issue in a tricky way.

      → Ответить
»
7 лет назад, # |
← Rev. 2   Проголосовать: нравится +11 Проголосовать: не нравится

For each elephant at position x we keep a black node at position x and a white node at position x + L and connect the black node to the white node. Every white node is connected to the node with the next larger position (Break ties by the indices of the elephants.). If we maintain all nodes in set, we can find that node in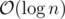 . This construction guaranties that every node has a degree of at most 3. (One edge from the next lower white node, one edge from a black node and one edge to the next node.)

To do queries, we keep an imaginary white node at  - ∞ and an imaginary white node at  + ∞ (which is the only white node that has no edge to a node at a larger position). The minimal number of cameras is given by the number of black nodes on the path from  - ∞ to ∞ (The greedy algorithm would place a camera starting at each black node on that path.). This is path-aggregate which can be computed in a link-cut tree in .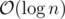

When an elephant moves, we need to delete it's black node and white node. For each of those nodes, at most one node may have an edge leading to it, so we need to fix the edges of at most 2 white nodes. Then we add it's black and white node at the new position, once again fix the edges of at most 2 white nodes and add the edge from it's white node. Adding or removing edges takes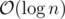 time in a link-cut tree, so the total runtime is .

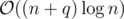There were some slides in an Asian language with some nice figures of the resulting tree of black and white nodes somewhere in the Internet, but I couldn't them the anymore.

→ Ответить