AtCoder Regular Contest 082 / Beginner Contest 072 will be held on Saturday (time). The writer is sigma425.
The point values will be
ABC: 100 — 200 — 300 — 400
ARC: 300 — 400 — 700 — 700
Let's discuss problems after the contest.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
AtCoder Regular Contest 082 / Beginner Contest 072 will be held on Saturday (time). The writer is sigma425.
The point values will be
ABC: 100 — 200 — 300 — 400
ARC: 300 — 400 — 700 — 700
Let's discuss problems after the contest.
| Name |
|---|



There's ARC from 21:00 JST and ends at 22:40 JST.
There's Topcoder Warsaw Regional Online Mirror (Fun SRM) from 22:00 JST and it is rated.
I like Atcoder problems and Topcoder problems very much, and both of them are my favorite contest site. So I want to participate both of them. I have to solve all problems of ARC within 60 minutes...
EDIT: Where did I get "rated" information from, is from topcoder slack.
Where do you find the information that the Fun SRM is rated? The TC emails don't even mention about the mirror contest...
What am I doing wrong? #pIn0Zm
(ConvexScore)
What do you calculate in the DP? I guess you find number of subsets of collinear points, but in a strange way.
Nope, I just calculate the thing from statement. I choose the bottom left point of the polygon, sort other possible vertices around it and calculate dp[vlast - 1][vlast] since any polygon with this bottom left point traversed clockwise can be constructed as subsequence of this array.
Answer is . This correction make it AC in
. This correction make it AC in 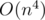 and
and  .
.
In the editorial for F, what do you mean by "Since the set of functions of the form above is closed under functions g1 and g2, ft is always of this form."?
It means that if before a step, the function is of this form, then after either applying the function g1 or g2, it will still be of this form.
Also, the constant a, b, c doesn't necessary to be the same for every t, right? Then, how can we calculate these constant while simulating the process?
You only need to calculate it at times t = t_i or t = r_i, for some i.
Between two of these consecutive times, either you apply g1 k times, or g2 k times. However, g_1(y) = max(y-1,0) composed k times is max(y-k,0).
I really can't understand the meaning of a,b,c :( :(
I will try to explain in a (hopefully) different way.
Consider the amount of sand in A (with a fixed starting value). When A is on top, this value decreases by one, unless it is already at 0. Similarly, if A is on top, it goes up by 1 unless it is at X.
Now let's look at the sequence of numbers (s_0, s_1, ... s_X), where s_v is the amount of sand if we started with v sand in A. Then look at how this sequence changes after each step. Here is an example with X = 7:
You can see that the sequences always looks like (a,a,a,a+1, a+2, ..., b-1, b, b) or similar and you just need to keep track of the values of a and b as well as where they start and end.
Did somebody solve F with sqrt decomposition and binsearch in O(n·sqrt(n)·log(sqrt(n)))? It's almost 109 operations in worst case in my code, but it passed in 0.5s.
I think there is mistake in English Editorial in F
"is either g1(y) = max(y − 1, 0) (in case A is above B) or g2(y) = max(y + 1, X) (in case B is above A)"
I think g2(y) should be min(y+1,X)
Here is a generalization of E (ConvexScore).
Can someone please elaborate more on the solution in editorial of E:ConvexStore?
I am unable to understand how only counting the sets which doesn't contain a subset of collinear points enough to calculate the answer.
As is common on Atcoder, this problem also features a very nice (maybe easy to some, but I couldn't figure during contest) if-and-only-if observation. Note that the problem is trivially equivalent to counting, for each convex set (defined in the statement), the number of subsets of the set of points lying inside or on it except the vertices themselves (2n - S). As is to be expected, this is counted differently for the solution. It says that it is sufficient to count sets for which the convex hull has a positive area. Formally the problem requires us to count pairs (X, U) such that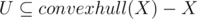 . But consider
. But consider 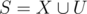 . From this we can uniquely determine X = points - in - convex - hull(S), U = S - X. This works as suppose we can add another element from U to X, then X contain a superfluous element, which by definition (no collinear points) are not allowed. On the other hand, (X, U) obviously uniquely determines
. From this we can uniquely determine X = points - in - convex - hull(S), U = S - X. This works as suppose we can add another element from U to X, then X contain a superfluous element, which by definition (no collinear points) are not allowed. On the other hand, (X, U) obviously uniquely determines 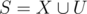 , proving that S → (X, U) is a bijection, thus their cardinalities are the same.
, proving that S → (X, U) is a bijection, thus their cardinalities are the same.
Next, note that all such S are nothing but all sets with positive area of convex hull, each counted only once, as S obviously have positive area of convex hull, and each set with positive convex hull can be used to write such an S.
Now to count convex hulls with positive area, it is necessary to opposite-count, thats is count sets with 0 area, and that is trivial.
It is a very nice problem, and it was completely non-obvious to me at first. I was like "what a terrible contest, C and D are super easy and E looks like very ugly geometry and F is some segment-tree bullshit". But both problems turned out to be interesting and relatively straightforward implementation-wise.
And I really really hoped that I'll be double red this weekend, but ... well ... 2798 :-D
First, note that we don't really need to know how much sand there is in bulb B since it's just X minus the amount of sand in bulb A. Every time bulb A is on top, it loses 1 unit of sand each second, until it has 0 sand left. Similarly, when it is at the bottom, it gains 1 unit of sand each second, until it has X units of sand left.
Let f(x) denote the amount of sand bulb A will contain if it starts with x units of sand. We'll keep track of this function every time we flip the bulb.
The key is to note that the function f can always be defined by 4 integers (actually one of them can be computed from the other 3 but we'll keep all 4 for convenience), mn, mx, l, r. f(x) = mn if x < l, f(x) = mn + x - l if l ≤ x ≤ r and f(x) = mx if x > r.
Initially, f(x) = (0, X, 0, X).
Let's see how the function change when we flip the sandglass after v seconds. Suppose before we flip the sandglass, bulb A is losing sand. Thus, bulb A will lose v units of sand in total during this period. Suppose previously f(x) = (mn, mx, l, r).
If v ≤ mn, then the new function is g(x) = (mn - v, mx - v, l, r), as it's just the entire function shifted down by v units.
If v > mn, then the values l, r might change, since the function goes below 0 after shifting down by v units and we need to make the front part become 0 again. You can check that in this case, the new function is g(x) = (0, max(mx - v, 0), min(l + v - mn, X), max(min(l + v - mn, X), r)).
If bulb A gains sand for v seconds, we can update the function in a similar manner.
Thus, we can update the function in O(1) for each time period.
Now, to answer each query (t, v), where t is the amount of time passed and v is the initial amount of sand in bulb A, let's binary search to find the largest time y ≤ t where the sandglass is last flipped. Plug in v into the function at time y (which we precomputed in the beginning for all moments we flip the sandglass) to get the amount of sand in bulb A after y seconds in O(1). Then, depending on the parity of the number of flips performed, we add or subtract the amount of sand in bulb A by t - y (taking max with 0 or min with X if needed) to get the final amount of sand in bulb A. Thus, each query can be answered in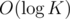 time.
time.
can u pls explain what mn, mx, l, r denote??
The parameters that define the function. f will be defined as a function equal to
mn if x < l
mn + x - l if l ≤ x ≤ r
and mx if x > r.
i meant to ask why initially (mn, mx, l, r) = (0, X, 0 ,X)??
f(x) = x for all 0 ≤ x ≤ X before we flip anything.