Georeth's blog

A Tree Problem Made By Me
By Georeth, history, 8 years ago, In English

Hello, I made a very classic tree problem. I want to get some clean solutions, because my solution seems very complicated. I made this problem on Polygon, but cannot make it public to every one. So I publish this problem here.

I hope you can give me good solutions (maybe by ideone.com / or join my group).

I create a group called "problem sharing" at http://codeforces.me/group/t0m8sIZmgT. You can join this group to solve this problem.

Maximum weight vertex for a fixed distance
time limit per test
2 seconds
memory limit per test
64 megabytes
input
standard input
output
standard output

Given a tree with n vertices and a positive integer D. Vertices are numbered from 1 to n. Each vertex u has a positive weight wu.

For each vertex u, compute ans[u] = max{wv: dist(u, v) = D}. if such vertex v does not exist, ans[u] =  - 1.

Where dist(u, v) is length of shortest path between u and v.

Input

First line contains integer n and D. (1 ≤ n ≤ 100000, 1 ≤ D ≤ 100).

Second line contains n integers w1, w2, ..., wn. (1 ≤ wi ≤ 109)

Then (n - 1) lines follow. Each line contains two integer u and v, which means there is an edge (u, v).

Output

Output n intergers in a single line. i-th of them should be ans[i].

Examples
Input
5 2
1 3 4 2 5
1 2
2 3
3 4
4 5
Output
4 2 5 3 4
Input
5 2
1 3 7 2 5
1 5
2 5
3 5
4 5
Output
7 7 3 7 -1
  • Vote: I like it
  • +55
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it +6 Vote: I do not like it

Well there is a pretty neat and easy solution in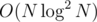 with centroid decomposition and a segment tree or Fenwick for prefix maximum. And it will work for any value of D.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +8 Vote: I do not like it

    Yes，but I have an O(N*D) solution just use tree DP. So I make a constraint for D.

    Plz submit your solution. I want to see your code.

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +24 Vote: I do not like it

    Actually, the approach using the centroid decomposition can be simply implemented to run in time. No need for segment tree.

    → Reply
»
8 years ago, # |
← Rev. 4   Vote: I like it +5 Vote: I do not like it

I submitted a solution using Centroid Decompsition, it took 311 ms

The idea was to store for each centroid an array of sets, the kth set correspond to nodes at distance k from the centroid and of course, the array size is <= D

The query checks the greatest value in the sets of the centroids it visits on its way up the tree

I also used a sparse table to calculate lca(u, v) in O(1)

The same idea can be used to solve Timus — Tree2

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I have got 4 accepted submissions.

3 of them use centroid decomposition O(N log N) or O(N log2 N). Another uses a O(N * D) DP Technique and is cleaner than my own solution.

Thanks.

→ Reply