Итак, начнём разбор.
219A - k-String
Давайте для каждой буквы l посчитаем, сколько раз она встретилась в строке --- массив c[l]. Подсчет осуществляется примерно так: c[s[i]]++. Если количество вхождений какой-то буквы не кратно k, то мы уже сразу понимаем, что составить нужную нам строку невозможно. Теперь построим строку p: добавим в неё 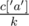 букв 'a',
букв 'a', 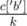 букв 'b', и так далее. Выведем полученную строку k раз.
букв 'b', и так далее. Выведем полученную строку k раз.
219B - Special Offer! Super Price 999 Bourles!
Переберем количество девяток на конце числа от 1 до 18. Пусть эта величина равна k. В таком случае максимальное число не превосходящее заданное p можно получить так:
- сотрем последние k цифр числа x: = p / 10k
- добавим справа k девяток y: = x·10k + 10k - 1
- если значение y больше p, то уменьшим число x (то, что идет до k девяток) на 1 и к результату допишем k девяток y: = (x - 1)·10k + 10k - 1
Если получившееся y > = p - d, то обновим ответ значением k.
219C - Color Stripe
Разберём 2 два случая:
- k равно 2. Тогда нам подходят только две строки — чередующиеся буквы 'A' и 'B'. Выбираем из них тот, который требует меньшего числа перекрасок.
- k больше 2. Возьмем самый левый блок из одинаковых букв. Пусть его длина равна k, тогда надо не менее k / 2 перекрашиваний, чтобы избавиться от соседних одинаковых клеток в этом блоке. Если k нечетно, то можно каждую вторую клетку в блоке перекрасить в любой из цветов, отличных от цвета блока. Если k четно, то можно делать тоже самое, но аккуратнее выбрать цвет: он должен отличаться не только от цвета блока, но и от цвета следующей клетки за блоком. Это всегда возможно сделать, так как количество цветов больше 2.
219D - Choosing Capital for Treeland
Для того, чтобы решить эту задачу посчитаем для каждого города количество ребер, которые надо переориентировать, чтобы данный город стал столицей.
В задаче были достаточно большие ограничения, поэтому нельзя было просто посчитать все эти значения n обходами в глубину. Авторское решение запускает только два обхода в глубину. Первым обходом в глубину посчитаем ответ для города номер 1. Заметим, что если посчитан ответ для вершины x, то ответ для вершины y, которая соединена с x, можно посчитать за O(1). А именно, ans(y) = ans(x) - direction(x, y) + (1 - direction(x, y)), где direction(x, y) — равно 1, если ребро (x, y) ориентировано не так как во входных данных, и равно 0, иначе.
Пользуясь описанным фактом, можно посчитать все значения ans(v) одним обходом, зная ans(1).
Итоговая ассимптотика решения O(n).
219E - Parking Lot
Будем поддерживать две структуры: множество отрезков свободных парковочных мест, в котором отрезки отсортированы по их началу, и множество отрезков свободных парковочных мест отсортированных по размеру. Такие структуры должны поддерживать операцию быстрого поиска первого больше либо равного элемента, удаление элемента и его вставку, нахождениe максимума и следующего по величине элемента.
В языке C++, авторское решение использовало set <pair<int,int>> и map <int, set<int>>. Set отрезков и Map из длины отрезка в набор отрезков с заданной длиной. Операция поиска больше либо равного элемента в этих структурах называется lower_bound.
Научимся поддерживать эти структуры от операции к операции. Для того, чтобы определить автомобилиста на стоянку, нужно взять свободный отрезок с максимальной длиной или с (максимальной длиной минус один), который не упирается в начало или конец стоянки, и попробовать определить автомобилиста на свободное парковочное место в середину этого отрезка (если точной середины нет, то в ближайшую к ней клетеку). Среди всех таких позиций нужно выбрать наилучшую (в смысле условия задачи). После нахождения лучшей позиции надо разрезать соотвествующий отрезок свободных позиций на два и обновить обе структуры (удалить старый отрезок и вставить два новых).
Чтобы удалить автомобилиста со стоянки нужно добавить новый отрезок свободных парковочных мест длины один в структуру. Предварительно нужно удалить смежные с этим отрезком отрезки в структуре. Соединить их с нашим отрезком и добавить один большой отрезок в структуру.
Отдельные случаи возникает при рассмотрении крайних отрезков.
Итоговая сложность решения O(m log n)











спасибо) хороший контест)
А ведь контест и правда отличный) Спасибо авторам) Очень понравилась Д)
Я на Д для каждого ребра добавлял по единичке для всех вершин либо в поддереве, либо во всем остальном графе, в зависимости от направления ребра. O(NlogN), правда...:)
В C можно было написать двумерную динамику. Где dp[i][j] — минимальное количество перекрашиваний в полоске длины i, оканчивающейся на символ j.
Сложность O(n*k^2). Правда заходит на грани TL :)
Ну можно заметить, что нам из предыдущего столбца нужен минимум только, а если минимум в той же букве что и текущая, то второй минимум, а это за линию предпосчитывать можно, итого O(n*k). 2054589
Я считал минимум на префиксе и минимум на суффиксе. То есть для j-го символа брал минимум из префикса длины j — 1 и суффикса, начинающегося в позиции j + 1. 2059006. Некоторые моменты, конечно, можно сделать попроще.
все извращались как могли
Если я правильно понял пояснение к задаче про цены, то там опечатка. Из пояснения видно, что к — максимальное количество 9 на конце и оно же выводится в ответ "обновим ответ значением k", но в ответ требуется y. Поправьте меня если я не прав.
Да, похоже должно быть "обновим значеним у")
В задаче D:
Асимптотика должна быть O(N log N) из-за сортировки ответа, разве нет? (Опечатка в тексте — асимптотика с одним 'с' )
P.S. Вот я неудачник, у меня она упала как раз из-за того, что забыл sort в конце. И кроме того, мой текущий рейтинг — 1699.
Для поиска минимума в массиве изобретён более эффективный алгоритм. Почитайте Кормена.
"Во вторую строку выведите все возможные способы выбрать столицу — последовательность номеров городов в порядке возрастания."
Для сортировки натуральных чисел от 1 до n изобретён более эффективный алгоритм. Почитайте Кормена.
Уговорил. Читать Кормена вовсе не обязательно.
Уговорил. Не читай Кормена.
Можно обойтись без этого, если перебирать вершины в порядке возрастания номера.
O RLY?
Классный контест! Мне очень понравился! Очень интересно было, когда у многих (да и у меня тоже) на системном тестировании выпала третья задачка (нужно было просто еще немного подумать).
Кстати, это был личный контест, а не командный :)
Вопрос по задаче D: объясните, пожалуйста, как поиском в глубину из 1-й вершины найти ответ для этой вершины?
Ответ для нее равен количеству ребер, которые во время обхода проходились не в том направлении, в котором они заданы в ориентированном графе.
То есть, я должен делать обход в неориентированном графе и запоминать все ребра по которым я прохожу?
В неоринентированном графе, да. Давайте для каждой вершины посчитаем величину "количество ребер, идущих не в том направлении в поддереве вершины". Тогда ответ для листьев равен 0, для остальных вершин — сумма по всем сыновьям + количество ребер, идущих в сыновей и направленных не в ту сторону.
Их количество
Вы идете как по неориентированному ребру, но, если вы вдруг пошли по ребру не в том направлении, то это ребро надо перенаправить, то есть к ответу прибавляется 1. И dfs возвращает, собственно, ответ для поддерева. Что вы имеете в виду под "запоминать все ребра"?
А кто может подсказать способ решение задачи E на Pascal. Какие структуры использовать?