Graph saving methods

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	164
1	maomao90	164
3	Um_nik	163
4	atcoder_official	160
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
8	Dominater069	154
8	nor	154

Hi.

Introduction.

We have a graph, we want to save it (and maybe run DFS on it for example); simple? Yes, but I want to show different methods for this, you can choose any of them depending on problem.

Adjacency matrix.

Simple, if graph is not weighted, save in G[v][u] if there is an edge between v and u or not.

If graph is weighted, if there is an edge between v and u save it’s weight in G[v][u], save - 1 otherwise (if weight can be negative, use inf instead of - 1).

Memory usage : 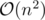$\text{[math]}$ .
Overall time complexity : 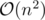$\text{[math]}$ (for running dfs).

Code here

// God & me

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e3 + 17;
int n, m;
bool G[maxn][maxn], mark[maxn];
void dfs(int v){
    if(mark[v])  return ;
    mark[v] = 1;
    for(int u = 0; u < n; u++)
	if(G[v][u])
	    dfs(u);
}
int main(){
    ios::sync_with_stdio(0), cin.tie(0);
    cin >> n >> m;
    for(int i = 0; i < m; i++){
	int v, u;
	cin >> v >> u;
	G[v][u] = G[u][v] = 1;
    }
    return 0;
}

Vectors.

It's the most common method for saving graph. For each vertex keep a vector of it’s edges, now for each edge just save it in related vectors. Use pair (or another struct) for saving weighted graph. It works similar for directed graph.

Memory usage : 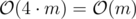$\text{[math]}$ (Note that vector uses more memory than you need).
Overall time complexity : 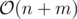$\text{[math]}$ (for running dfs).

Code here

// God & me

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 17;
int n, m;
bool mark[maxn];
vector<int> G[maxn];
void dfs(int v){
    if(mark[v])  return ;
    mark[v] = 1;
    for(auto u : G[v])  dfs(u);
}
int main(){
    ios::sync_with_stdio(0), cin.tie(0);
    cin >> n >> m;
    for(int i = 0; i < m; i++){
	int v, u;
	cin >> v >> u;
	G[v].push_back(u);
	G[u].push_back(v);
    }
    return 0;
}

Dynamic array.

This method is rarely used. For each vertex count edges connected to it at first, then allocate a enough space for each vertex to save it’s adjacency-list. Note that this method is Offline.

Memory usage : 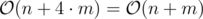$\text{[math]}$ .
Overall time complexity : 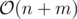$\text{[math]}$ (for running dfs).

Code here

// God & me

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 17;
int n, m;
bool mark[maxn];
int *G[maxn], sz[maxn];
pair<int, int> edge[maxn];
void dfs(int v){
    if(mark[v])  return ;
    mark[v] = 1;
    for(int i = 0; i < sz[v]; i++)
	dfs(G[v][i]);
}
int main(){
    ios::sync_with_stdio(0), cin.tie(0);
    cin >> n >> m;
    for(int i = 0; i < m; i++){
	int v, u;
	cin >> v >> u;
	sz[v]++, sz[u]++;
	edge[i] = {v, u};
    }
    for(int i = 1; i <= n; i++){
	G[i] = new int[ sz[i] ];
	sz[i] = 0;
    }
    for(int i = 0; i < m; i++){
	int v = edge[i].first, u = edge[i].second;
	G[v][ sz[v]++ ] = u;
	G[u][ sz[u]++ ] = v;
    }
    return 0;
}

Linked list.

This method is used when id of edges are important and works only for directed graphs (or if you can convert the undirected graph to directed). We use array for saving edges. Then, for each vertex we keep index of last added edge and for each edge consider it’s from From_i to To_i, we keep the index of last edge before this edge that From_index = From_i and name it prv_i. Then we can use head_v and prv array to find adjacency-list.

Memory usage : 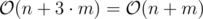$\text{[math]}$ .
Overall time complexity : 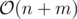$\text{[math]}$ (for running dfs).

Code here

// God & me

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 17;
int n, m, from[maxn], to[maxn], head[maxn], prv[maxn];
bool mark[maxn];
void dfs(int v){
    if(mark[v])  return ;
    mark[v] = 1;
    for(int e = head[v]; e != -1; e = prv[e])
	dfs(to[e]);
}
int main(){
    ios::sync_with_stdio(0), cin.tie(0);
    cin >> n >> m;
    fill(head, head + n, -1);
    for(int i = 0; i < m; i++){
	int v, u;
	cin >> v >> u;
	from[i] = v, to[i] = u;
	prv[i] = head[v];
	head[v] = i;
    }
    return 0;
}

Application: Solving flow network problems. Wikipedia: Maximum flow problem.

Naive implementation

void add_edge(int v, int u, int vu, int uv = 0){
    to[ecnt] = u, prv[ecnt] = head[v], cap[ecnt] = vu, head[v] = ecnt++;
    to[ecnt] = v, prv[ecnt] = head[u], cap[ecnt] = uv, head[u] = ecnt++;
}
int dfs(int v, int flow = inf){
  if(v == sink || flow == 0)  return flow;
  if(mark[v])  return 0;
  mark[v] = 1;
  for(int e = head[v]; e != -1; e = prv[e])
    if(cap[e]){
      int x = dfs(to[e], min(flow, cap[e]));
      if(x)
	return cap[e] -= x, cap[e ^ 1] += x, x;
    }
  return 0;
}
int maxflow(){
  int ans = 0;
  for(int tmp; (tmp=dfs(so)); ans += tmp)
	memset(mark, 0, sizeof mark);
  return ans;
}

Dinic’s blocking flow algorithm

void add_edge(int v, int u, int vu, int uv = 0){
    to[ecnt] = u, prv[ecnt] = head[v], cap[ecnt] = vu, head[v] = ecnt++;
    to[ecnt] = v, prv[ecnt] = head[u], cap[ecnt] = uv, head[u] = ecnt++;
}
bool bfs(int source, int sink){
    memset(dis, 63, sizeof dis);
    dis[source] = 0;
    int h = 0, t = 0;
    q[t++] = source;
    while(h < t){
	int v = q[h++];
	for(int e = head[v]; e != -1; e = prv[e])
	    if(cap[e] && dis[ to[e] ] > dis[v] + 1){
		dis[ to[e] ] = dis[v] + 1, q[t++] = to[e];
		if(to[e] == sink)  return 1;
	    }
    }
    return 0;
}
int dfs(int v, int sink, int flow = inf){
    if(v == sink || flow == 0)  return flow;
    int ret = 0;
    for(int &e = ptr[v]; e != -1; e = prv[e])
	if(dis[v] == dis[ to[e] ] - 1){
	    int x = dfs(to[e], sink, min(flow, cap[e]));
	    flow -= x, ret += x;
	    cap[e] -= x, cap[e ^ 1] += x;
	    if(flow == 0)  break;
	}
    return ret;
}
int max_flow(int source, int sink){
    int ans = 0;
    while(bfs(source, sink)){
	memcpy(ptr, head, sizeof ptr);
	ans += dfs(source, sink);
    }
    return ans;
}

Usage of this method in above codes are where we use cap[e] -= x, cap[e ^ 1] += x. Because of special adding edge method, it is guaranteed that if edge e is from v to u, 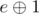$\text{[math]}$ is its pair and it’s from u to v.

Related submission : 23115110.

Index keeping.

This method is used when index of edges is important (i.e. in queries we need to change something about edges, i.e. change weight, delete edge). Keep index of edges related to each vertex in its vector, and for each edge keep the vertices connecting with this edge (see code below).

Note that index keeping is possible and maybe easier using map (or unordered_map), but it is faster using this method. Also note that dynamic array method could be used here as well.

Memory usage : 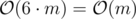$\text{[math]}$ (Note that vector uses more memory than you need).
Overall time complexity : 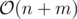$\text{[math]}$ (for running dfs).

Code here

// God & me

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 17;
int n, m;
int first[maxn], second[maxn];
vector<int> g[maxn];
void dfs(int v){
    if(mark[v])  return ;
    mark[v] = 1;
    for(auto e : g[v]){
	int u = first[e] == v ? second[e] : first[e];  // or simply first[e] + second[e] - v, or first[e] ^ second[e] ^ v;
	dfs(u);
    }
}
int main(){
    ios::sync_with_stdio(0), cin.tie(0);
    cin >> n >> m;
    for(int i = 0; i < m; i++){
	int v, u;
	cin >> v >> u;
	g[v].push_back(i);
	g[u].push_back(i);
	first[i] = v, second[i] = u;
    }
    return 0;
}

Example: Consider you need to change weight of edges online, this is simple using index keeping method, but it isn’t possible with other methods (at least it will be harder). Related submission : 20776118.

Application: Finding Euler tour. Wikipedia : Eulerian path. Blocking edges is easier with this method, that’s what we need in Euler tour finding. Related submissions : 21395473, 21636007.

Comparison.

I used Codeforces polygon for comparing and generated 16 random graphs:

#1 to #4 : n = 10⁶, m = 10⁶
#5 to #4 : n = 10⁵, m = 10⁶
#9 to #8 : n = 10⁴, m = 10⁶
#13 to #16 : n = 10³, m = 10⁶

#	dynamic array	linked list	vector
1	OK 1637 / 44	OK 1123 / 29	OK 1606 / 39
2	OK 1637 / 44	OK 1247 / 29	OK 1559 / 39
3	OK 1590 / 44	OK 1107 / 29	OK 1560 / 39
4	OK 1669 / 44	OK 1169 / 29	OK 1622 / 39
5	OK 1060 / 29	OK 1060 / 31	OK 1169 / 36
6	OK 1106 / 29	OK 1045 / 31	OK 1123 / 36
7	OK 1060 / 30	OK 1029 / 31	OK 1122 / 36
8	OK 1091 / 29	OK 1044 / 31	OK 1169 / 36
9	OK 1029 / 26	OK 1013 / 29	OK 1044 / 29
10	OK 982 / 26	OK 998 / 29	OK 1013 / 29
11	OK 1013 / 26	OK 982 / 29	OK 1201 / 29
12	OK 1123 / 26	OK 1029 / 29	OK 1029 / 29
13	OK 998 / 26	OK 951 / 29	OK 982 / 27
14	OK 935 / 26	OK 982 / 29	OK 950 / 27
15	OK 951 / 26	OK 951 / 29	OK 982 / 27
16	OK 966 / 26	OK 1060 / 29	OK 1013 / 27
Σ	16	16	16
max.	1669ms / 44MB	1247ms / 31MB	1622ms / 39MB

It's really strange for me that vector uses less memory than dynamic array while testing, can someone explain the reason? Here is the link to codes and generator.

UPD: I found the answer, I missed that in dynamic array method we are saving edges in pairs, and keeping the sz array in addition (thanks to ATofighi).

As usual I’d like to finish the post with a poem:

بی سبب هرگز نمی‌گردد کسی یار کسی
یار بسیار است تا گرم است بازار کسی

By: Parto biza’ee arani.

Translation: No one becomes friend with another one without reason. People are like shops, a shop is full of customers while it has goods.

P.S. Kindly write in comments (or use private chat in case of necessary) if something is wrong.

Комментарии (4)

Написать комментарий?

radoslav11

8 лет назад, # |

It really doesn't seem right that the vector representation uses less memory. Can you provide both codes (for the tests generators and for the representations alone).

→ Ответить

Arpa

8 лет назад, # ^ |

← Rev. 2 →

I'll add them now.

Edit: Done.

gepardo

← Rev. 4 →

It's really strange for me that vector uses less memory than dynamic array while testing, can someone explain the reason?

Maybe storing the edges in the dynamic array method (you have 10⁶ edges) eats additionally 8 MB of memory? And using dynamic arrays instead of vectors saves some memory (~3MB) so the dynamic array variant eats 5MB bigger.

M.A.H.M.O.O.D

There's a way to store trees only which is by having an array par and saving the parent of the i-th node int par[i].

Блог пользователя Arpa

Introduction.

Adjacency matrix.

Vectors.

Dynamic array.

Linked list.

Index keeping.

Comparison.