Hi!
Here are some implementations for solving RMQ (Tarjan’s algorithm) (Range Maximum / Minimum Query).
It’s very simple to implement and its time complexity is O((n + q)·a(n)), a() stands for Akerman inverse function used in DSU.
Problem: Given array a of n integers, and q queries, for each query print the maximum value in range [L, R].
Solution: We need an array of vectors, called assigned. assigned[r] contains queries that their R is r. When getting queries, push each query in assigned[R]. We need a dsu, first pari is i. We need a stack, named st.
For i from 0 to n, do:
While st is not empty and a[st.top] <= a[i]
Set i parent of st.top in dsu and pop this element from st.
Push i to st
For each query assigned to i
The answer to this query is a[root of L of this query in DSU].
// God & me
// "Someone like you"?! Unbelievable ...
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 17;
int par[maxn], ans[maxn], n, a[maxn], l[maxn], q;
vector<int> qu[maxn];
int root(int v){
return par[v] == -1 ? v : par[v] = root(par[v]);
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
memset(par, -1, sizeof par);
cin >> n;
for(int i = 0; i < n; i++) cin >> a[i];
cin >> q;
for(int i = 0, r; i < q; i++){
cin >> l[i] >> r, r--, l[i]--;
qu[r].push_back(i);
}
stack<int> st;
for(int i = 0; i < n; i++){
while(st.size() && a[st.top()] <= a[i])
par[st.top()] = i, st.pop();
st.push(i);
for(auto qi : qu[i])
ans[qi] = a[root(l[qi])];
}
for(int i = 0; i < q; i++)
cout << ans[i] << ' ';
cout << '\n';
return 0;
}
Note that in the above code I used the path-compression technique for dsu only, size-comparing technique can be used too (but it has lower performance).
It’s obviously true because each time for any j ≤ i, a[root(j)] is the greatest value in range [j, i].
Performance test
// God & me
// "Someone like you"?! Unbelievable ...
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1 << 22;
int par[maxn], ans[maxn], n, a[maxn], l[maxn], q, head[maxn], prv[maxn], st[maxn], tail;
int root(int v){
return par[v] == -1 ? v : par[v] = root(par[v]);
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
memset(par, -1, sizeof par);
memset(head, -1, sizeof head);
cin >> n;
for(int i = 0; i < n; i++) cin >> a[i];
cin >> q;
for(int i = 0, r; i < q; i++){
cin >> l[i] >> r, r--, l[i]--;
prv[i] = head[r], head[r] = i;
}
for(int i = 0; i < n; i++){
while(tail-- && a[ st[tail] ] <= a[i])
par[ st[tail] ] = i;
st[++tail] = i;
for(int qi = head[i]; qi >= 0; qi = prv[qi])
ans[qi] = a[root(l[qi])];
}
for(int i = 0; i < q; i++)
cout << ans[i] << ' ';
cout << '\n';
return 0;
}
// God & me
// "Someone like you"?! Unbelievable ...
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1 << 22;
int n, q, a[maxn], ans[maxn], head[maxn], prv[maxn], l[maxn];
vector<int> v, qu[maxn];
int main(){
ios::sync_with_stdio(0), cin.tie(0);
memset(head, -1, sizeof head);
cin >> n;
for(int i = 0; i < n; i++) cin >> a[i];
cin >> q;
for(int i = 0, r; i < q; i++){
cin >> l[i] >> r;
prv[i] = head[r], head[r] = i;
}
for(int i = 0; i < n; i++){
while(v.size() && a[v.back()] <= a[i]) v.pop_back();
v.push_back(i);
for(int qi = head[i]; qi >= 0; qi = prv[qi])
ans[qi] = a[*lower_bound(v.begin(), v.end(), l[qi])];
}
for(int i = 0; i < q; i++)
cout << ans[i] << ' ';
cout << '\n';
return 0;
}
// God & me
// "Someone like you"?! Unbelievable ...
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1 << 22, lg = 22;
int par[maxn], ans[maxn], n, q, lg2[maxn];
int spt[lg][maxn];
int main(){
ios::sync_with_stdio(0), cin.tie(0);
memset(par, -1, sizeof par);
cin >> n;
for(int i = 0; i < n; i++)
cin >> spt[0][i];
for(int i = 2; i < n; i++) lg2[i] = lg2[i >> 1] + 1;
for(int k = 1; k < lg; k++)
for(int i = 0; i + (1 << k) <= n; i++)
spt[k][i] = max(spt[k - 1][i], spt[k - 1][i + 1 << (k - 1)]);
cin >> q;
for(int i = 0, l, r; i < q; i++){
cin >> l >> r, r++;
cout << max(spt[ lg2[r - l] ][l], spt[ lg2[r - l] ][ r - (1 << lg2[r - l]) ]) << ' ';
}
cout << '\n';
return 0;
}
// God & me
// "Someone like you"?! Unbelievable ...
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1 << 22;
template<typename Val, typename Compare = std::less<Val>, int BlockSize = 10>
class DirectRMQ {
public:
typedef int Index; //今のところ大きくともintを仮定している(queryとか)
typedef char InBlockIndex;
typedef InBlockIndex(*BlockTypeRef)[BlockSize];
DirectRMQ(Compare comp_ = Compare()) :
blockTypes(0), innerBlockTable(0), sparseTable(0) {
comp = comp_;
calcBallotNumbers();
buildInnerBlockTable();
}
~DirectRMQ() {
delete[] innerBlockTable;
delete[] blockTypes; delete[] sparseTable;
}
void build(const Val *a, Index n) {
blocks = (n + BlockSize - 1) / BlockSize;
stHeight = 0; while(1 << stHeight < blocks) ++ stHeight;
delete[] blockTypes; delete[] sparseTable;
blockTypes = new BlockTypeRef[blocks];
calcBlockTypes(a, n);
buildInnerBlockTable(a, n);
sparseTable = new Index[blocks * stHeight];
buildSparseTable(a);
}
//[l,r]の閉区間
Index query(const Val *a, Index l, Index r) const {
Index x = l / BlockSize, y = r / BlockSize, z = y - x;
if(z == 0) return x * BlockSize + blockTypes[x][l % BlockSize][r % BlockSize];
if(z == 1) return assumeleft_minIndex(a,
x * BlockSize + blockTypes[x][l % BlockSize][BlockSize - 1],
y * BlockSize + blockTypes[y][0][r % BlockSize]);
z -= 2;
Index k = 0, s;
s = ((z & 0xffff0000) != 0) << 4; z >>= s; k |= s;
s = ((z & 0x0000ff00) != 0) << 3; z >>= s; k |= s;
s = ((z & 0x000000f0) != 0) << 2; z >>= s; k |= s;
s = ((z & 0x0000000c) != 0) << 1; z >>= s; k |= s;
s = ((z & 0x00000002) != 0) << 0; z >>= s; k |= s;
return assumeleft_minIndex(a
, assumeleft_minIndex(a,
x * BlockSize + blockTypes[x][l % BlockSize][BlockSize - 1],
sparseTable[x + 1 + blocks * k])
, assumeleft_minIndex(a,
sparseTable[y + blocks * k - (1 << k)],
y * BlockSize + blockTypes[y][0][r % BlockSize])
);
}
Val queryVal(const Val *a, Index l, Index r) const {
Index x = l / BlockSize, y = r / BlockSize, z = y - x;
if(z == 0) return a[x * BlockSize + blockTypes[x][l % BlockSize][r % BlockSize]];
Val edge = minVal(
a[x * BlockSize + blockTypes[x][l % BlockSize][BlockSize - 1]],
a[y * BlockSize + blockTypes[y][0][r % BlockSize]]);
if(z == 1) return edge;
z -= 2;
Index k = 0, s;
s = ((z & 0xffff0000) != 0) << 4; z >>= s; k |= s;
s = ((z & 0x0000ff00) != 0) << 3; z >>= s; k |= s;
s = ((z & 0x000000f0) != 0) << 2; z >>= s; k |= s;
s = ((z & 0x0000000c) != 0) << 1; z >>= s; k |= s;
s = ((z & 0x00000002) != 0) << 0; z >>= s; k |= s;
return minVal(edge, minVal(
a[sparseTable[x + 1 + blocks * k]],
a[sparseTable[y + blocks * k - (1 << k)]]));
}
private:
Compare comp;
int ballotNumbers[BlockSize + 1][BlockSize + 1];
InBlockIndex(*innerBlockTable)[BlockSize][BlockSize];
Index blocks;
int stHeight;
BlockTypeRef *blockTypes;
Index *sparseTable;
inline Index minIndex(const Val *a, Index x, Index y) const {
return comp(a[x], a[y]) || (a[x] == a[y] && x < y) ? x : y;
}
inline Index assumeleft_minIndex(const Val *a, Index x, Index y) const {
return comp(a[y], a[x]) ? y : x;
}
inline Val minVal(Val x, Val y) const {
return comp(y, x) ? y : x;
}
void buildSparseTable(const Val *a) {
Index *b = sparseTable;
if(stHeight) for(Index i = 0; i < blocks; i ++)
b[i] = i * BlockSize + blockTypes[i][0][BlockSize - 1];
for(Index t = 1; t * 2 < blocks; t *= 2) {
std::memcpy(b + blocks, b, blocks * sizeof(Index));
b += blocks;
for(Index i = 0; i < blocks - t; ++ i)
b[i] = assumeleft_minIndex(a, b[i], b[i + t]);
}
}
void buildInnerBlockTable(const Val *a, Index n) {
for(Index i = 0; i < blocks; i ++) {
BlockTypeRef table = blockTypes[i];
if(table[0][0] != -1) continue;
const Val *p = getBlock(a, n, i);
for(InBlockIndex left = 0; left < BlockSize; left ++) {
Val minV = p[left];
InBlockIndex minI = left;
for(InBlockIndex right = left; right < BlockSize; right ++) {
if(comp(p[right], minV)) {
minV = p[right];
minI = right;
}
table[left][right] = minI;
}
}
}
}
//端っこのブロック用に関数内staticなテンポラリ配列を返す
const Val *getBlock(const Val *a, Index n, Index i) {
Index offset = i * BlockSize;
if(offset + BlockSize <= n)
return a + offset;
else {
static Val tmp_a[BlockSize];
std::copy(a + offset, a + n, tmp_a);
Val maxVal = Val();
for(Index j = i; j < n; j ++) //iでなくoffsetでは?(動作には問題ないし計算量もほとんど変わらないけれど…)(バグるのが嫌なので(今まで動いていたので)直すのは後にする)
if(comp(maxVal, a[j])) maxVal = a[j];
std::fill(tmp_a + (n - offset), tmp_a + BlockSize, maxVal);
return tmp_a;
}
}
void calcBlockTypes(const Val *a, Index n) {
Val tmp_rp[BlockSize + 1];
for(Index i = 0; i < blocks; i ++)
blockTypes[i] = calcBlockType(getBlock(a, n, i), tmp_rp);
}
BlockTypeRef calcBlockType(const Val *a, Val *rp) {
int q = BlockSize, N = 0;
for(int i = 0; i < BlockSize; i ++) {
while(q + i - BlockSize > 0 && comp(a[i], rp[q + i - BlockSize])) {
N += ballotNumbers[BlockSize - i - 1][q];
q --;
}
rp[q + i + 1 - BlockSize] = a[i];
}
return innerBlockTable[N];
}
void calcBallotNumbers() {
for(int p = 0; p <= BlockSize; p ++) {
for(int q = 0; q <= BlockSize; q ++) {
if(p == 0 && q == 0)
ballotNumbers[p][q] = 1;
else if(p <= q)
ballotNumbers[p][q] =
(q ? ballotNumbers[p][q - 1] : 0) +
(p ? ballotNumbers[p - 1][q] : 0);
else
ballotNumbers[p][q] = 0;
}
}
}
void buildInnerBlockTable() {
int numberOfTrees = ballotNumbers[BlockSize][BlockSize];
innerBlockTable = new InBlockIndex[numberOfTrees][BlockSize][BlockSize];
for(int i = 0; i < numberOfTrees; i ++)
innerBlockTable[i][0][0] = -1;
}
};
int n, q, a[maxn];
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for(int i = 0; i < n; i++)
cin >> a[i];
DirectRMQ<int> rmq;
rmq.build(a, n);
cin >> q;
for(int i = 0, l, r; i < q; i++){
cin >> l >> r;
cout << rmq.queryVal(a, l, r) << ' ';
}
cout << '\n';
return 0;
}
// God & me
// "Someone like you"?! Unbelievable ...
#include <bits/stdc++.h>
using namespace std;
const int n = 1 << 22;
int a[n];
int main(){
ios::sync_with_stdio(0), cin.tie(0);
srand(time(0));
cout << n << '\n';
iota(a, a + n, 0);
random_shuffle(a, a + n); // used for generating random test
for(int i = 0; i < n; i++)
cout << a[i] << " \n"[ i == n - 1 ];
cout << n << '\n';
for(int i = 0; i < n; i++){
int l = rand() % n, r = rand() % n;
if(l > r) swap(l, r);
cout << l << ' ' << r << '\n';
}
return 0;
}
Here is the result:
| Method\Time(milliseconds) | Strictly increasing array | Strictly decreasing array | Random |
| This method (known as Arpa's trick) | 2943 | 2890 | 2946 |
| Sparse table | 3612 | 3595 | 3807 |
| Vector + Binary search | 3101 | 6130 | 3153 |
| O(n) method | 3788 | 3920 | 3610 |
Update (Feb 2025): The above method is actually 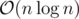 . Refer to this blog for
. Refer to this blog for  algorithm.
algorithm.










I know this technique as "Arpa's trick". Are you sure you've got the right name?
I discovered this technique myself, but it seems this technique existed before (as Zlobober said). So I can't name this technique "Arpa's trick", but I call it "Arpa's trick", you can call it "Arpa's trick" as well.
At least he's helping others ... You can also write tutorials and name techniques using your fake name . Are you sure you wrote "lucian bicsi" correctly ?
Fake name ?! In fact, "Arpa" is compressed version of my name, my real name is "AmirReza PoorAkhavan", my friends call me Arpa at school, chat, etc. I'm more familiar with "Arpa" instead of my real name ("PoorAkhavan" or "AmirReza").
There are much persons, knowing me as "Arpa", and don't know my real name even.
I was talking about I_love_Retrograd
Oh right ! But your comment prepared a opportunity for me to talk about my nick name :D
Edit: sorry anyway.
You could also binary search on the stack instead of using DSU, which might be easier to code depending on the implementation, and still achieve a reasonable performance (binary searches are pretty light).
I'll add some statistics about what method is faster soon, please wait for several hours.
Edit: Done.
Can anyone please explain the vector+binary search approach for this problem or provide any source where i can learn the approach. Thank you.
Iterate over the elements of the array, and answer all queries that end in the current element. And you maintain a decreasing vector with the elements (and indices), on which you can binary search to find the answer.
Think of it this way, if you fixate the right boarder and look at the RMQs
[0, R], [1, R], [2, R], ..., [R, R], then you can notice that the RMQs are monotone decreasing. I.e.RMQ(0, R) >= RMQ(1, R) >= RMQ(2, R) >= ... >= RMQ(R, R). In the vector you maintain the list of all values that appear in that RMQ list, together with their most-left index.If you add a new element (so you go from
RtoR+1), you just need to look at how the RMQs change, since now you want the list to reflect the RMQs for[0, R+1], ..., [R+1, R+1]. Which means if the new element in the array is smaller than the previous minimum, then you can just add the element to the vector, as all the previous R+1 RMQs don't change, and the last one will have the RMQA[R+1]. But if the element is bigger, then you need to delete a few of the previous RMQs from the list, since by adding that element their RMQ will get bigger.The example code from Arpa should explain the details.
You can outline header of the table like this:
Code:
Ok, I found this post, it's too old but anyway. If someone finds it in the future. It's said:
"Note that in above code I used path-compression technique for dsu only, size-comparing technique can be used too (but it has lower performance)."
But only path-compression works in $$$O(\log n)$$$ time. So if you want it to work in $$$a(n)$$$ time, you need to use both path-compression and size-comparing techniques.
That's true, but in this algorithm we force links, not merge two sets. Thus using rank heuristic can't be applied in this algorithm, which leaves us with O*(log(n)) asymptotics per query. In detail: https://cs.stackexchange.com/a/108793
Sorry, I didn't understand your point. Could you extend it, please?
All I wanted to say is that this approach can't use the full power of the DSU's heuristics, therefore O*(alpha(n)) asymptotics is unreachable.
Huh? It's easy to implement merge-by-rank or merge-by-size here. It might be slower at practical input sizes, though, especially for non-malicious input.
Doing so just involves tracking the "intended" roots (the largest value in each merged range) as a summary statistic in the actual structural roots of each tree.
I think I know how to implement this using both optimizations. I will do it after the snackdown round, if nobody does it before and if I do not forget
Uh, I was going to write blogpost about this :D
Idea is the following: each DSU set contains segment of element between the stack entries. Each time we pop something from the stack, we merge segments that element was separating by merging the corresponding sets in DSU.
I don't really understand what's the difference between this approach and the initial one
Idk, I wanted to say that the only difference should be that we also store the maximal value of the whole component in its dsu representative
The idea is the same: each dsu tree knows it's rightmost element. Yet order of linking actually doesn't matter so one can just merge correponding components.