ma5termind's blog

HackerRank HourRank-15
By ma5termind, history, 8 years ago, In English

Hi Codeforces,

I am taking this opportunity to announce HackerRank HourRank 15, a 60 minute contest where the fastest coder wins!. The contest will be held on 16:30 UTC Saturday, 3rd December, 2016. You can sign up for the contest here. Contestants will be given 4 problems and 1 hour to solve. I recommend all of you to read all the problems as each problem contains some interesting subtasks. Top 10 global winners will get cool HackerRank T-shirts. Note that contest will be rated for all users.

As you can probably guess, i am author of this contest and i promise you all to deliver an interesting problem set with something for all. I really want to thank danilka.pro for testing all the problems and helping me to come up with nice problem set. My special thanks to Shafaet for bringing me back to problem setting and motivate me to work hard for this contest. Also, thanks to svanidz1 for presolving the contest and providing his valuable feedback.

Scoring will be posted right before the contest and editorials will be published right after the contest.

Hope to see you participating.

Good Luck & Have Fun.

UPDATE 1: Score Distribution 15-35-70-80.

UPDATE 2: Contest will be started in less than 25 minutes. See you guys on leaderboard.

UPDATE 3: Contest will be started in less than 5 minutes. All the best.

UPDATE 4: Contest has started. May the force is with you :).

UPDATE 5: Contest has ended. Editorials are uploaded. Thank you for participating. I am eagerly waiting to have your feedback guys.

  • Vote: I like it
  • +46
  • Vote: I do not like it

Comments Comments (37)
| Write comment?
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve the third problem?

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it -19 Vote: I do not like it

    I had a O(n2 / 2) DP but that only gets 42? Is expected solution better than that? :/

    Mine is to have state DP(pairs, non-pairs) where pairs is number of elements that exist is pairs, and non-pairs is number of element that dont. We have 2 option: Either put an element that exist in pair or one that doesnt. For option 1, we add DP(pair-1, non-pair+1) and subtract DP(pair-1, non-pair) and for option 2 we simply add DP(pair, non-pair-1).

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Fake account of NibNalin

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      For option1, you add DP(pair-1, non-pair+1) and subtract DP(pair-1, non-pair) why? Help me understand that why you are subtracting DP(pair-1, non-pair).
      According to me, when we put an element from pair we don't want next element to be same so we should subtract DP(pair-1 ,1).
      I know I am wrong somewhere, can you please help me to clear this.

      → Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +5 Vote: I do not like it 
    dp[a][b][c] = ((1 — c) * (a * dp[a — 1][b][0] + b * dp[a + 1][b — 1][1]) + c * ((a — 1) * dp[a — 1][b][0] + b * dp[a+1][b-1][1])) % mod

    the answer will be dp[number_of_numbers_which_appear_once][number_of_numbers_which_appear_twice][0]

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I don't know how it is solved so good, for me it was pretty hard. I got idea and couldn't code on the time. Here is my idea:

    First remove single elements, we will add them at the end it is easy...

    Now we will calculate DP[ i ][ j ] number of permuations with first i pairs such that we have exactly j neighbours. Answer is DP[ number of pairs] [ 0 ]. How we can caluclate this DP, we can see all possible situations of previous condition and adding that two elements ( in that station we can come from stations DP [i-1] [ j -1] , DP [i-1] [ j ], DP [i-1] [ j + 1], DP [i-1] [ j +2] )...

    I didn't read editorial, but I believe this is correct.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      This was initial dp approach i had and this is correct.

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Cool, now I will finish coding :)

        I really like this task, one of my favourite in last time :)

        Still I can not believe that 62 coders solved it in one hour, I thought I am really smart when I invented this :D

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          I did the same but took some time even more than you.

          → Reply
          • »
            »
            »
            »
            »
            »
            8 years ago, # ^ |
              Vote: I like it +3 Vote: I do not like it 
            I can't understand the editorial.How did you derive the 1st equation: dp[i][j] = dp[i][j] + dp[i-1][j]*i ?? why multiplied by 'i'? I don't find it correct for following case: 1 1 2, suppose we add '3'. Now the set of elements is {1,1,2,3), so i=2,j=1. Now, dp[2][1]= dp[2-1][1]*2 = 1*2 = 2 = wrong.
correct permutations are more: 3121,1321,1231,1213 ..
            → Reply
            • »
              »
              »
              »
              »
              »
              »
              8 years ago, # ^ |
                Vote: I like it +1 Vote: I do not like it

              First equation says that number of ways such that a permutation ends at one of the single element. We can choose the last element in i ways because there are exactly i such elements and multiply it with the number of permutating i-1 single elements and j double elements. Does this makes sense ?

              → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I did almost the same, but failed the second sample. You can't just add the single elements at the end — they might affect the answer.

      1 1 2

      If you process the pair (1, 1) and then process 2 seperatly you'll find that the answer is 0.
      Sorry if I misunderstood your solution
      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
        ← Rev. 3   Vote: I like it 0 Vote: I do not like it

        Well, when you put all pairs, let's say we have 2x numbers now. We still need to add n-2x elements. Each of them we can place at one position from 1..2x+1 ( at total 2x+1 positions ). First we have n! ways to permutate it ( we will multiply answer with n! at the end and suppose that we know order of all single elements). Now our task is making increasing sequence of n — 2x elements, each in range [1..2x+1], that is also simple dp. DP1 [i] [j] number of ways to have increasing sequence of i elements and last is j.

        I hope I will code it a little later :)

        → Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +1 Vote: I do not like it

    Let's count the permutations which don't satisfy the statement and then subtract this number from the number of all permutations. dp[i][j] — number of permutations of i elements, j of which occur twice, such that there is at least one pair of adjacent equal numbers. dp[i][0] is 0 for any i. To calculate dp[i][j], there are the following possibilities:

    1. Use some element which occurs once. This can be done only if 2 * j < i. The state we go to is dp[i - 1][j].

    2. Use some element which occurs twice, but use only one of its occurrences. We go to state dp[i - 1][j - 1] and multiply it by j, because we have j possible elements to choose from. Note that we should now subtract dp[i - 2][j - 1] * j because we don't want to put both of the equal elements here.

    3. Put some pair of equal elements here, which immediately makes all possible permutations bad. We have j possible pairs to choose from. Once we choose such pair, we remain with i - 2 elements, from which there are j - 1 pairs of equal elements. And all such permutations are bad. So we simply add .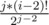

    → Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +16 Vote: I do not like it

    I didn't use DP but combinatorics instead.

    Firstly, the number of permutations of a multiset having N elements, including M duplications, is N!/(2^M). Let's denote M as the total number of duplications in the initial multiset.

    Let's calculate the number of permutations having at least K successive equal pairs:

    - There are R=(N-K*2) remaining elements which do not belongs to these pairs.
- There are (M_choose_K * K!) ways to select and order the pairs.
- There are R!/(2^(M-K)) ways to order the remaining elements.
- There are (K+R)_choose_K ways to "merge" the selected pairs with the remaining elements.

    The formula is (M_choose_K * K!) * R!/(2^(M-K)) * (K+R)_choose_K.

    Then I used the inclusion-exclusion principle to obtain the answer.

    My code: http://pastebin.com/B2ZsF4Zc

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +9 Vote: I do not like it

    Can be solved in O(n) using inclusion-exclusion principle. Lets say there are c distinct elements with count 2, then answer is sum(ncr(c,i)*(n-i)!/pow(2,c-i)) for all i= 0 to c. Code

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +19 Vote: I do not like it

    I just solved it using dp(i)(j)(b) -> Processing i pairs, j individual elements, with b true if the last element was the first of a pair.

    dp(i,j,b):
 if b == false:
  return i * bt(i - 1, j + 1, true) + j * bt(i, j - 1, false)
 else if b == true:
  return  i * bt(i - 1, j + 1, true) + (j-1) * bt(i, j - 1, false)

    Then the answer would be dp(number_of_pairs, number_of_numbers_which_appear_once, false).

    I coded this dp inside the contest but I had j=0 and I was thinking of a way to add the individual elements after this dp :( I WAS SO CLOSE
    My AC code: pastebin

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Could you please explain a little more what true/false means?

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      This approach should be added in editorial. I did understand this solution whereas editorialst solution involves too much Maths.

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Please explain to me as well :)

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
          ← Rev. 2   Vote: I like it +6 Vote: I do not like it

          The code is self-explanatory. Firstly, count number of pairs elements and non-pairs elements. In one step we can put a pair element or non-pair element.
          If we choose to put pair element then next state would be solve(pair-1, nonPair+1) (By putting an element from pair we have increase nonPair element by 1). (There are pairC1 ways to choose to any element from pair). Moreover we do not want next element to be same as this element so we mark a boolean variable as true.

          If we choose to put nonPair element then next state would be solve(pair, nonPair-1). (If boolean variable is mark as false than there are nonPairC1 ways to choose, If it is mark as true then we can choose any element except one i.e. there are (nonPair-1)C1 ways to choose.

          Code
          → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it -8 Vote: I do not like it

    I use stupid solution (n**2)q and it got accepted.

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

sosad only solve the fourth problem after contest. But the test case seems a bit weak as my solution is O(k * deg(u)2).

→ Reply
»
8 years ago, # |
  Vote: I like it +10 Vote: I do not like it

Does somebody know where can I read about the exact way how "don't do too many submissions" model works at HackerRank? I.e. how often one can submit codes without being punished and what's exact triggering criteria of getting error message? For me it was frustrating today to get a message "The rate of your submission is very high. Please try again in 2 minutes." and then stumble on it again several minutes later while key part of my strategy to solve last problem was in spamming server with a lot of versions of trashy solution :)

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can't we see others' code in Hackerrank?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    We unlocked the codes, now you can see them in submissions tab.

    → Reply
»
8 years ago, # |
  Vote: I like it -18 Vote: I do not like it

A bit off-topic but I realized how weak I am in solving dp problems.
Can anyone suggest a good way to start off with dp?
I tried solving the dp-tagged questions on cf but most of the time the editorials use a different technique and I'm not able to get the final answer through dp.
Thanks in advance.

→ Reply
»
8 years ago, # |
  Vote: I like it +16 Vote: I do not like it

Feedback:
Entertaining and interesting contest. I enjoyed it very much and I would recommend it to a friend. No uninteresting/pointless problems (unlike the current Week Of Code contest)

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    What is your criteria in determining whether the problem is pointless or not?

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In 4th task, why this formula dis(u,v) = abs(depth[u]-depth[lca(u,v)]) + abs(depth[v]-depth[lca(u,v)]), gives wrong answer?

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In the last problem's editorial, what does "sorting by tin" mean ? I had never seen that expression before.

→ Reply