Hello!
What is the fastest way to calc the number of divisors of n! , s.t 1 <= n <= 1e8.
Number of test cases <= 5000 .
I've stucked at this point while solving this problem EasyFact
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3857 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3463 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Qingyu | 158 |
| 5 | atcoder_official | 157 |
| 5 | Um_nik | 157 |
| 7 | adamant | 151 |
| 7 | djm03178 | 151 |
| 7 | luogu_official | 151 |
| 10 | awoo | 146 |
Hello!
What is the fastest way to calc the number of divisors of n! , s.t 1 <= n <= 1e8.
Number of test cases <= 5000 .
I've stucked at this point while solving this problem EasyFact
| Name |
|---|



Auto comment: topic has been updated by The-Legend (previous revision, new revision, compare).
Auto comment: topic has been updated by The-Legend (previous revision, new revision, compare).
What's wrong with prime factorization? Since the number of test cases <= 5000, you should pre-calculate the prime factorization of all numbers <= 10^8. Now use this to answer each test case in sqrt(n) * log(n).
.
Prime divisors of N! (N factorial) are less or equal to N. So, for each prime P ( <= N), you can calculate its power in factorization of N! using this code:
There are 5 millions primes up to 1e8, for each one of them I need to calling " calc " , and this is for one test case , it's too slow.
You only need to check primes upto since the power of all primes greater than
since the power of all primes greater than  in n! will be 1. And you can precalculate how many primes are in the range
in n! will be 1. And you can precalculate how many primes are in the range 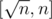
Yeah got it. How to solve for higher n?
UPD:I've misunderstood the problem.Ignore this comment,thanks.
You are wrong.
I want N! not N
Try this case
T = 1;
N = 5;
then N! = 120 = 2^3 * 3 * 5 then the number of divisors equal to 16
Your answer is 2
We need to find for all primes in range [1, N] powers in which that numbers occurs in the N!'s factorization. For primes from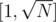 it`s clear. For any prime
it`s clear. For any prime 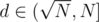 (lets call that set "big primes") we can observe, that d's power in factorizations of numbers from [1, N] is only 0 or 1. Thus d's power in the answer equal to amount of numbers in [1, N] which d devides. Lets call that power p(d). Then we can observe that all numbers with same value of p(·) is a consecutive segment of "big primes" and moreover p(·) has only
(lets call that set "big primes") we can observe, that d's power in factorizations of numbers from [1, N] is only 0 or 1. Thus d's power in the answer equal to amount of numbers in [1, N] which d devides. Lets call that power p(d). Then we can observe that all numbers with same value of p(·) is a consecutive segment of "big primes" and moreover p(·) has only 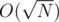 values.
values.
Amount of big primes with fixed p(d) (= amount of primes with exactly p(d) multiples) equals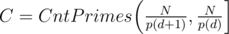 . Any of them gives p(d) + 1 to the answer thus in the result we need to assign ans = ans * (p(d) + 1)C.
. Any of them gives p(d) + 1 to the answer thus in the result we need to assign ans = ans * (p(d) + 1)C.
I`m sure that my explanation was really ugly and I hope code will be useful.
Thanks :)
Maybe can help.