Can someone please explain how to solve this problem https://www.hackerearth.com/march-clash-15/algorithm/counting-on-tree-1/description/ using centroid tree decomposition.
→ Pay attention
Before contest
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
4 days
Register now »
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
4 days
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/26/2024 23:11:05 (k1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










I really liked the problem and after a bit thinking I think I found a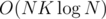 solution with centroid decomposition. The main idea is that each time after we pick a new centroid with dynamic programming we look at the number of beautiful subsets with our centroid included in them.
solution with centroid decomposition. The main idea is that each time after we pick a new centroid with dynamic programming we look at the number of beautiful subsets with our centroid included in them.
First idea which comes to our mind is to root the current subgraph at the centroid and then do dynamic programming with state dp[u][k'] = number of subsets with root u and sum of values k'. The most basic way is to make for every state O(K) transitions so overall complexity of the dp will be O(NK2). And then complexity of the solution will be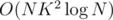 .
.
By the way this dp is actually a valid solution to the problem. We can simply pick an arbitrary vertex of our tree as a root and do the dp. Then the answer will be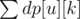 . And the complexity will be O(NK2).
. And the complexity will be O(NK2).
Lets go back to our centroid decomposition solution. To make it more efficient. We will change the dynamic programming to dp[i][k'] = number of subsets on the first i vertices with root equal to our centroid with sum of values k'. By "first i" I mean first i in dfs order. It's not hard to do this in O(NK) time. So in such a way we create an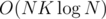 solution.
solution.